建堆时间复杂度

本文主要是介绍建堆时间复杂度，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

片头

嗨！小伙伴们，大家好！在上一篇中，我们学习了什么是堆，以及如何实现堆。这一篇中，我将继续带领大家来深入学习堆，准备好了吗？我要开始咯！

首先，大家还记得这个代码吗？

//堆的初始化
void HeapInit(Heap* hp) {assert(hp);		//断言,防止传入空指针hp->arr = NULL; //动态数组为空hp->capacity = 0;//初始时,数组的容量为0hp->size = 0;	 //初始时,数组的大小为0
}

哈哈，是的！这就是我们初始化堆的代码，那我们今天同样是初始化堆，但是思路和之前不太一样哦！

首先，我们定义一个接口函数 HeapCreate,里面包含3个参数，分别是 Heap* hp, ElemType* arr, int n，函数的返回类型为 void

void HeapCreate(Heap* hp,ElemType* a,int n);

三个参数的意义如下：

Heap* hp: 指向堆这个结构体的指针，用来对堆进行修改操作
ElemType* arr: 指向外界提供数组的指针
int n: n表示要在arr数组拷贝的元素个数

关于这个接口函数，具体实现代码如下：

//堆的构建
void HeapCreate(Heap* hp, ElemType* a, int n) {assert(hp);            //断言，防止传入空指针assert(a);             //断言，防止传入空指针//对堆这个结构体的成员变量arr开辟一块空间(堆的本质就是数组）hp->arr = (ElemType*)malloc(sizeof(ElemType)*n);//开辟n个大小的空间if (hp->arr == NULL) {    //如果内存空间不足perror("malloc fail！\n");exit(1);}memcpy(hp->arr, a, n * sizeof(ElemType));//将数组a的所有元素拷贝到堆的arr中hp->capacity = n;//初始化堆的容量为nhp->size = n;    //初始化堆的元素个数为n//建堆//向上调整建堆/*for (int i = 1; i < hp->size; i++) {        //从第二个结点开始挪动AdjustUp(hp->arr, i);}*///向下调整建堆for (int i = (hp->size - 1 - 1) / 2; i >= 0; i--) {    //从倒数第一个非叶子结点开始挪动AdjustDown(hp->arr, hp->size, i);}
}

测试代码如下：

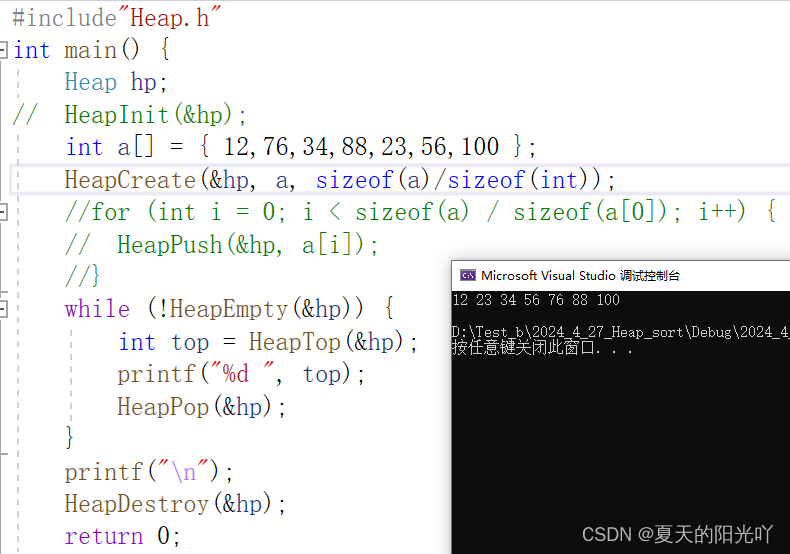
内容我们很熟悉，但是同样都是建堆，向上调整建堆和向下调整建堆有什么差异呢？它们两个进行比较，哪一个算法更优一点呢？

不急，且听我慢慢道来~

我们先来看看向上调整建堆

我们以满二叉树来举例子，因为它是一种特殊的二叉树，其中每个非叶子节点都有两个子节点，并且所有叶子节点都在同一层上。

二叉树的每一层结点数目如下：

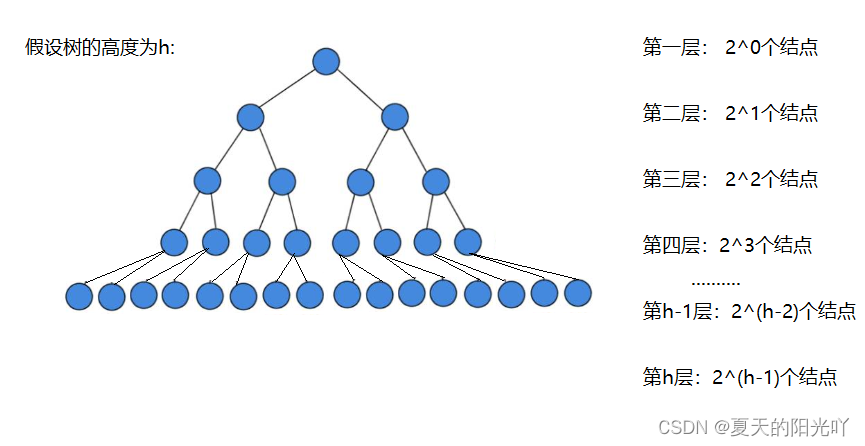
我们现在采用向上调整建堆的思想，创建的第一个结点可以看成小堆（大堆），因此，我们不需要对第一个结点作任何处理。创建第二个结点，我们就需要向上调整1次，创建第三个结点，我们就需要向上调整1次，因此，第二层总共有2个结点，我们需要调整1次，也就是 2^1*1。

因此，设累和向上调整F(H), F(H) = F(h1)+F(h2)+F(h3)+F(h4)+.......+F(h-1)+F(h) ,其中，F(h) = 每层结点个数 * 向上调整次数

所以，F(H) = 2^1*1 + 2^2*2 + 2^3*3 + ...... + 2^(h-2)*(h-2) + 2^(h-1)*(h-1) ,我们用错位相减法来求解此题

2*F(H) = 2^2*1 + 2^3*2 + 2^4*3 + ...... + 2^(h-2)*(h-3)+ 2^(h-1)*(h-2) + 2^(h)*(h-1)

F(H) = 2^1*1 + 2^2*2 + 2^3*3 + 2^4*4 + ....... + 2^(h-2)*(h-2) + 2^(h-1)*(h-1)

将两个式子相减：

2*F(H) - F(H) = -2^1 - 2^2 - 2^3 - 2^4 - ....... - 2^(h-2) - 2^(h-1) + 2^(h)*(h-1)

我们在等式中补充：-2^0 + 2^0 ，原式变成：-2^1 - 2^2 - 2^3 - 2^4 - ....... - 2^(h-2) - 2^(h-1) - 2^0 + 2^0 + 2^(h)*(h-1)，调换一下顺序，就变成下面这个样子：

2*F(H) - F(H) = - 2^0 - 2^1 - 2^2 - 2^3 - 2^4 - ....... - 2^(h-2) - 2^(h-1) + 2^0 + 2^(h)*(h-1)

F(H) = - （2^0 + 2^1 + 2^2 + 2^3 + 2^4 +.......+ 2^(h-2) + 2^(h-1) ）+ 2^0 + 2^(h)*(h-1)

【其中，2^0 + 2^1 + 2^2 + 2^3 + 2^4 +.......+ 2^(h-2) + 2^(h-1)，可以进行错位相减，设N是树中结点的数量，N = 2^0 + 2^1 + 2^2 + 2^3 + 2^4 +.....+ 2^(h-2) + 2^(h-1)

2*N = 2^1 + 2^2 + 2^3 + 2^4 + 2^5 +.....+ 2^(h-2) + 2^(h-1) + 2^(h)

2*N - N = 2^(h) - 2^0 = 2^h - 1

N = 2^h - 1, 2^h = N+1, h = log(N+1) (注意：本来是以2为底数，N+1为真数，但是也可以省略底数】

因此，上述可以化简为：F(H) = - (2^h-1) + 2^0 + 2^(h)*(h-1) = -2^h + 1 + 1 + 2^h*(h-1) F(H) = 2^h*(h-2) + 2, 将 F(H) 转换成 F(N) , 2^h = N+1, h = log(N+1) , F(N) =(N+1)*(log(N+1) -2) +2，F(N) = N*logN , 因此，向上调整建堆的时间复杂度为 O(N*logN)。

好啦，向上调整建堆的时间复杂度我们算出来了，那么向下调整建堆的时间复杂度怎么求呢？

还是以满二叉树来举例：

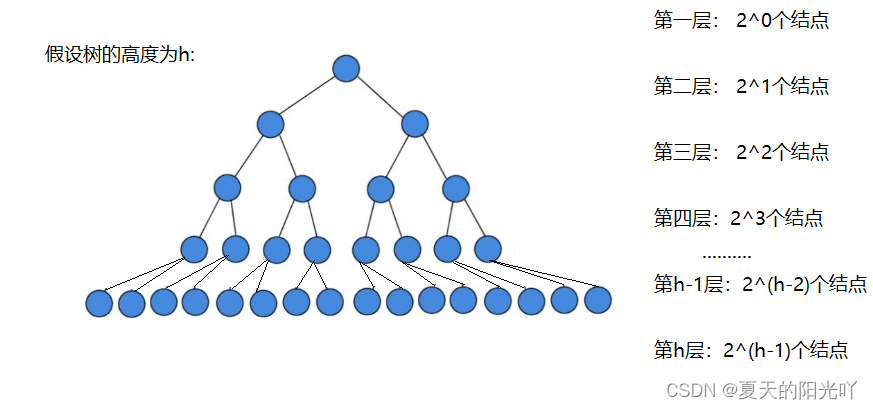
我们需要向下调整，建堆，最后一层（第h层）的叶子结点可以看作（大堆/小堆），所以我们不挪动叶子结点，因此，从倒数第一个非叶子结点开始挪动（也就是最后一个叶子结点的父节点），也就是第h-1层开始挪动，第h-1层的每一个结点最多向下调整1次，第h-2层的每一个结点最多向下调整2次，第h-3层的每一个结点最多向下调整3次,.........., 第5层的每一个结点最多向下调整h-5次，第4层的每一个结点最多向下调整h-4次，第3层的每一个结点最多向下调整h-3次，第2层的每一个结点最多向下调整h-2次，第1层的每一个结点最多向下调整h-1次。

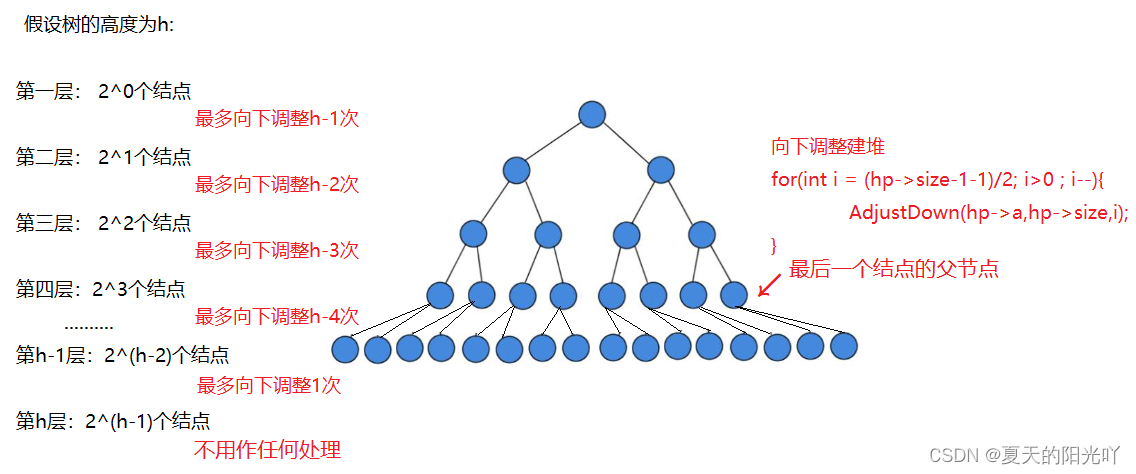
因此，设累和向下调整F(H), F(H) = F(h1)+F(h2)+F(h3)+F(h4)+.......+F(h-1)+F(h) ,其中，F(h) = 每层结点个数 * 向下调整次数

所以，F(H) = 2^(h-2)*1 + 2^(h-3)*2 + ...... + 2^3*(h-4) + 2^2*(h-3) + 2^1*(h-2) + 2^0*(h-1),我们用错位相减法来求解此题

F(H) = 2^(h-2)*1 + 2^(h-3)*2 + ...... + 2^3*(h-4) + 2^2*(h-3) + 2^1*(h-2) + 2^0*(h-1)

2*F(H) = 2^(h-1)*1 + 2^(h-2)*2 + ...... + 2^4*(h-4) + 2^3*(h-3) + 2^2*(h-2) + 2^1*(h-1)

将两个式子相减可得

2*F(H) - F(H) = 2^(h-1)*1 + 2^(h-2)*1 + 2^(h-3)*1 +......+ 2^4 + 2^3 + 2^2+ 2^1 - 2^0*(h-1)

F(H) = 2^(h-1)*1 + 2^(h-2)*1 + 2^(h-3)*1 +......+ 2^4 + 2^3 + 2^2+ 2^1 - (h-1)

F(H) = 2^(h-1)*1 + 2^(h-2)*1 + 2^(h-3)*1 +......+ 2^4 + 2^3 + 2^2 + 2^1 - h + 1 （这个“+1”可以看成 2^0）, 我们可以调换一下顺序：

F(H) = 2^0 + 2^1 + 2^2 + 2^3 + 2^4 +......+ 2^(h-3)*1 + 2^(h-2)*1 + 2^(h-1)*1 - h

【其中，2^0 + 2^1 + 2^2 + 2^3 + 2^4 +.......+ 2^(h-2) + 2^(h-1)，可以进行错位相减，设N是树中结点的数量， N = 2^0 + 2^1 + 2^2 + 2^3 + 2^4 +.....+ 2^(h-2) + 2^(h-1)

2*N = 2^1 + 2^2 + 2^3 + 2^4 + 2^5 +.....+ 2^(h-2) + 2^(h-1) + 2^(h)

2*N - N = 2^(h) - 2^0 = 2^h - 1

N = 2^h - 1, 2^h = N+1, h = log(N+1) (注意：本来是以2为底数，N+1为真数，但是也可以省略底数】

因此，上述可以化简为：F(H) = 2^h - 1 - h, 我们将 F(H) 转换为 F(N) , F(N) = (N+1) -1 - log(N+1) , F(N) = N - log(N+1) , 因此，向下调整建堆的时间复杂度为 O(N)。

向上调整建堆的时间复杂度为 O(N*logN) ，向下调整建堆的时间复杂度为 O(N)。那肯定是向下调整建堆的时间复杂度更小，因此我们会选择向下调整建堆。

哈哈哈，还有一种简便方法，那就是直接看图，不需要计算~ 你想想，假设树的高度为h, 满二叉树的最后一层叶子结点有多少个？前面我们画图分析过，最后一层叶子结点有 2^(h-1) 个, 那么整棵二叉树的结点总数有多少？设N是树中结点的数量， N = 2^h - 1，我们可以看到， 2^(h-1) 和2^h 只相差2倍，换句话说，最后一层的叶子结点占结点总数的1/2，如果我们采用向上调整算法，相当于整棵二叉树一半的结点都要挪动，是不是很费时？而如果我们采用向下调整算法，最后一层的叶子结点保持不动，只需要移动上面的结点，是不是要轻松很多？

设累和调整F(H), F(H) = F(h1)+F(h2)+F(h3)+F(h4)+.......+F(h-1)+F(h) ,其中，F(h) = 每层结点个数 * 调整次数 ，采用向上调整算法, 相当于 每层结点个数多 * 调整次数多（简称：多*多），采用向下调整算法，相当于 每层结点个数多 * 调整次数少或者每层结点个数少 * 调整次数多（简称：少*多或者多*少）

分析以上情况，我们可以得出：向下调整算法优于向上调整算法，所以如果要建堆，尽量选择向下调整算法。