本文主要是介绍Day22.一刷数据结构算法(C语言版) 216组合总和III；17电话号码的字母组合，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！
一、216组合总和III
如果把昨天的组合问题理解了，本题就容易一些了。
题目链接：组合总和III
文章讲解：代码随想录
视频讲解：和组合问题有啥区别？回溯算法如何剪枝？| 216.组合总和III
1.思路分析
相对于77. 组合，无非就是多了一个限制，本题是要找到和为n的k个数的组合，而整个集合已经是固定的了[1,...,9]。
本题k相当于树的深度，9（因为整个集合就是9个数）就是树的宽度。
例如 k = 2，n = 4的话，就是在集合[1,2,3,4,5,6,7,8,9]中求 k（个数） = 2, n（和） = 4的组合。
选取过程如图：
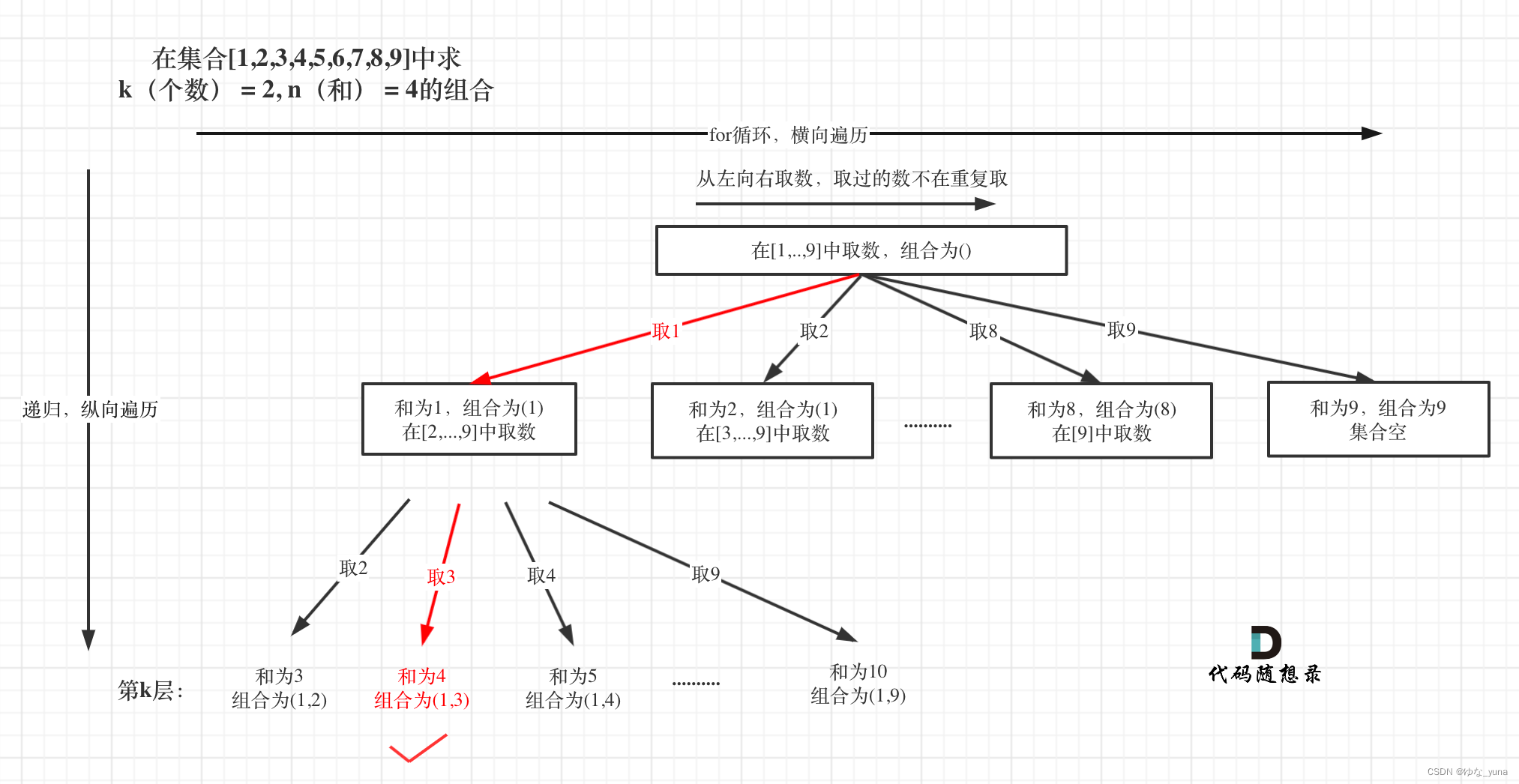
图中，可以看出，只有最后取到集合（1，3）和为4 符合条件。
回溯三部曲：
1）确定递归函数参数
本题依然需要一维数组path来存放符合条件的结果，二维数组result来存放结果集。
这里我依然定义path 和 result以及各自的栈顶指针pathTop、ansTop为全局变量。
至于为什么取名为path？从上面树形结构中，可以看出，结果其实就是一条根节点到叶子节点的路径。
int* path;
int pathTop;
int** ans;
int ansTop;接下来还需要如下参数：
- targetSum（int）目标和，也就是题目中的n。
- k（int）就是题目中要求k个数的集合。
- sum（int）为已经收集的元素的总和，也就是path里元素的总和。
- startIndex（int）为下一层for循环搜索的起始位置
void backtracking(int targetSum, int k, int sum, int startIndex) 还要强调一下，回溯法中递归函数参数很难一次性确定下来，一般先写逻辑，需要啥参数了，填什么参数。
2）确定终止条件
在上面已经说了，k其实就已经限制树的深度，因为就取k个元素，树再往下深了没有意义。
所以如果path.size() 和 k相等了，就终止。
如果此时path里收集到的元素和（sum） 和targetSum（就是题目描述的n）相同了，就用result收集当前的结果。
if(pathTop == k) {if(sum == targetSum) {int* tempPath = (int*)malloc(sizeof(int) * k);int j;for(j = 0; j < k; j++)tempPath[j] = path[j];ans[ansTop++] = tempPath;}// 如果path.size() == k 但sum != targetSum 直接返回return;}3）单层搜索过程
本题是集合固定的就是9个数[1,...,9]，所以for循环固定i<=9
如图：
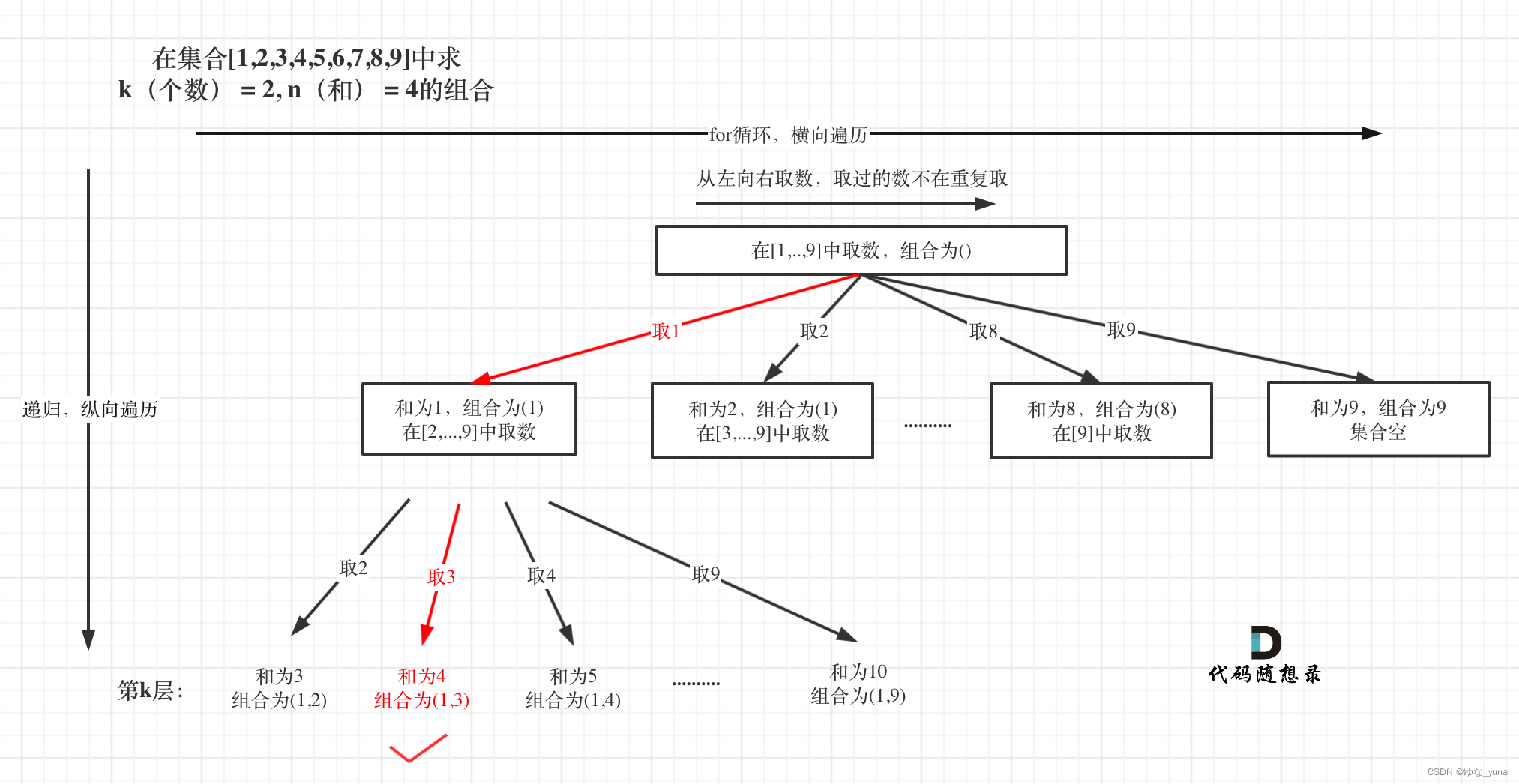处理过程就是 path收集每次选取的元素，相当于树型结构里的边，sum来统计path里元素的总和。
int i;//从startIndex开始遍历，一直遍历到9for (i = startIndex; i <= 9; i++) {sum += i; // 处理path[pathTop++] = i; // 处理backtracking(targetSum, k, sum, i + 1); // 注意i+1调整startIndexsum -= i; // 回溯pathTop--;; // 回溯}别忘了处理过程 和 回溯过程是一一对应的，处理有加，回溯就要有减！
2.代码详解
/*** Return an array of arrays of size *returnSize.* The sizes of the arrays are returned as *returnColumnSizes array.* Note: Both returned array and *columnSizes array must be malloced, assume caller calls free().*/
int* path;
int pathTop;
int** ans;
int ansTop;
int getPathSum() {int i;int sum = 0;for(i = 0; i < pathTop; i++) {sum += path[i];}return sum;
}void backtracking(int targetSum, int k, int sum, int startIndex) {if(pathTop == k) {if(sum == targetSum) {int* tempPath = (int*)malloc(sizeof(int) * k);int j;for(j = 0; j < k; j++)tempPath[j] = path[j];ans[ansTop++] = tempPath;}// 如果path.size() == k 但sum != targetSum 直接返回return;}int i;//从startIndex开始遍历，一直遍历到9for (i = startIndex; i <= 9; i++) {sum += i; // 处理path[pathTop++] = i; // 处理backtracking(targetSum, k, sum, i + 1); // 注意i+1调整startIndexsum -= i; // 回溯pathTop--;; // 回溯}
}int** combinationSum3(int k, int n, int* returnSize, int** returnColumnSizes){//初始化辅助变量path = (int*)malloc(sizeof(int) * k);ans = (int**)malloc(sizeof(int*) * 20);pathTop = ansTop = 0;backtracking(n, k, 0, 1);//设置返回的二维数组中元素个数为ansTop*returnSize = ansTop;//设置二维数组中每个元素个数的大小为k*returnColumnSizes = (int*)malloc(sizeof(int) * ansTop);int i;for(i = 0; i < ansTop; i++) {(*returnColumnSizes)[i] = k;}return ans;
}二、17电话号码的字母组合
本题大家刚开始做会有点难度，先自己思考20min，没思路就直接看题解。
题目链接：电话号码的字母组合
文章讲解：代码随想录
视频讲解：还得用回溯算法！| LeetCode：17.电话号码的字母组合
1.思路分析
这道题要解决如下三个问题：
数字和字母如何映射
两个字母就两个for循环，三个字符我就三个for循环，以此类推，然后发现代码根本写不出来
输入1 * #按键等等异常情况（力扣测试数据并没有涉及到这类情况，所以代码中暂时也不考虑，不过我们要知道有这些异常）
数字和字母如何映射：
这里定义一个二维数组，代码如下：
char* letterMap[10] = {"", //0"", //1"abc", //2"def", //3"ghi", //4"jkl", //5"mno", //6"pqrs", //7"tuv", //8"wxyz", //9
};回溯法来解决n个for循环的问题：
例如：输入："23"，抽象为树形结构，如图所示：
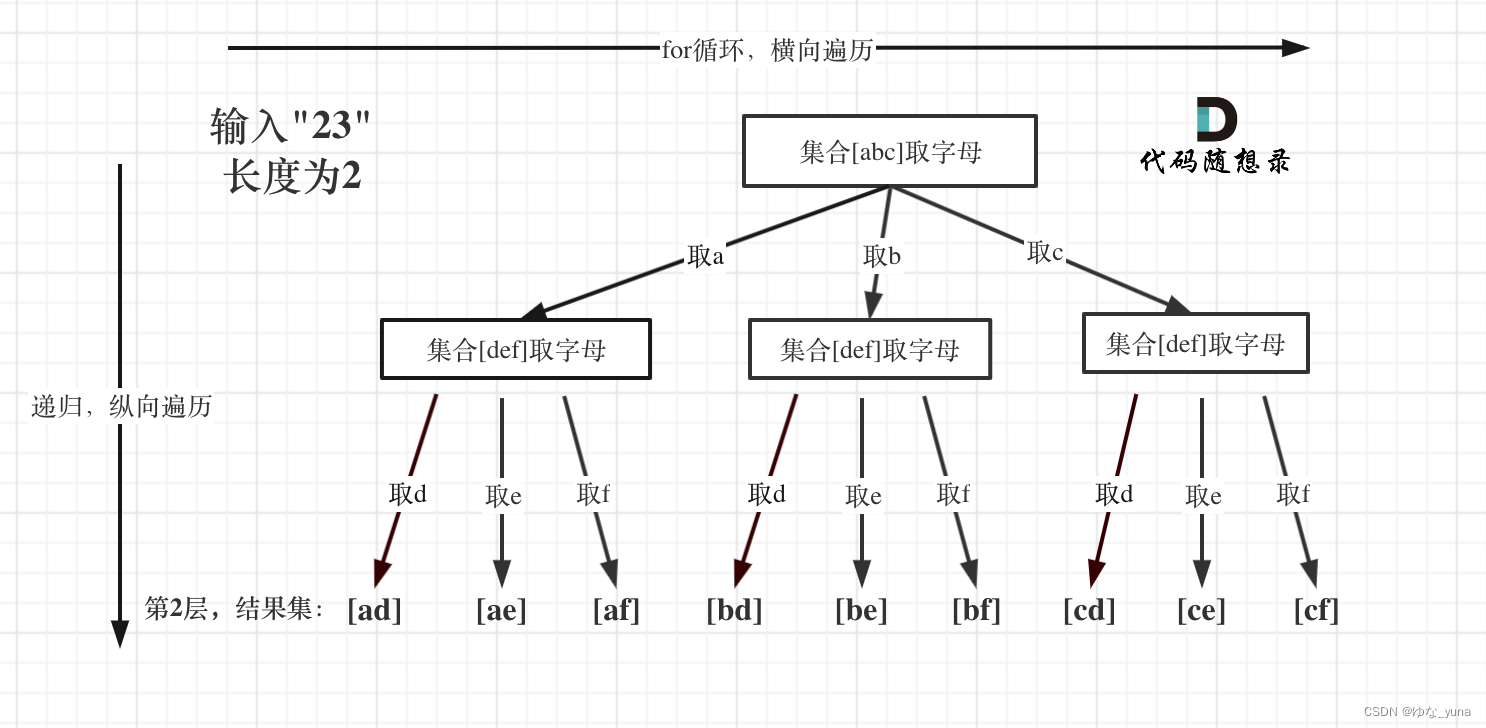图中可以看出遍历的深度，就是输入"23"的长度，而叶子节点就是我们要收集的结果，输出["ad", "ae", "af", "bd", "be", "bf", "cd", "ce", "cf"]。
回溯三部曲：
1）确定输入参数
首先需要一个字符串s来收集叶子节点的结果，然后用一个字符串数组result保存起来，这两个变量我依然定义为全局。别忘了还有对应栈顶指针。
再来看参数，参数指定是有题目中给的string digits，然后还要有一个参数就是int型的index。
注意这个index可不是 77.组合 和216.组合总和III 中的startIndex了。
这个index是记录遍历第几个数字了，就是用来遍历digits的（题目中给出数字字符串），同时index也表示树的深度。
char* path;
int pathTop;
char** result;
int resultTop;void backTracking(char* digits, int index)2）确定终止条件
例如输入用例"23"，两个数字，那么根节点往下递归两层就可以了，叶子节点就是要收集的结果集。
那么终止条件就是如果index 等于 输入的数字个数了（本来index就是用来遍历digits的）。
然后收集结果，结束本层递归。
//若当前下标等于digits数组长度if(index == strlen(digits)) {//复制digits数组，因为最后要多存储一个0，所以数组长度要+1char* tempString = (char*)malloc(sizeof(char) * strlen(digits) + 1);int j;for(j = 0; j < strlen(digits); j++) {tempString[j] = path[j];}//char数组最后要以0结尾tempString[strlen(digits)] = 0;result[resultTop++] = tempString;return ;}3）确定单层遍历逻辑
首先要取index指向的数字，并找到对应的字符集（手机键盘的字符集）。
然后for循环来处理这个字符集，代码如下：
//将字符数字转换为真的数字int digit = digits[index] - '0';//找到letterMap中对应的字符串char* letters = letterMap[digit];int i;for(i = 0; i < strlen(letters); i++) {path[pathTop++] = letters[i];//递归，处理下一层数字backTracking(digits, index+1);pathTop--;}注意这里for循环，可不像是在组合问题中从startIndex开始遍历的。
因为本题每一个数字代表的是不同集合，也就是求不同集合之间的组合，而组合问题是求同一个集合中的组合！
2.代码详解
/*** Note: The returned array must be malloced, assume caller calls free().*/
char* path;
int pathTop;
char** result;
int resultTop;
char* letterMap[10] = {"", //0"", //1"abc", //2"def", //3"ghi", //4"jkl", //5"mno", //6"pqrs", //7"tuv", //8"wxyz", //9
};
void backTracking(char* digits, int index) {//若当前下标等于digits数组长度if(index == strlen(digits)) {//复制digits数组，因为最后要多存储一个0，所以数组长度要+1char* tempString = (char*)malloc(sizeof(char) * strlen(digits) + 1);int j;for(j = 0; j < strlen(digits); j++) {tempString[j] = path[j];}//char数组最后要以0结尾tempString[strlen(digits)] = 0;result[resultTop++] = tempString;return ;}//将字符数字转换为真的数字int digit = digits[index] - '0';//找到letterMap中对应的字符串char* letters = letterMap[digit];int i;for(i = 0; i < strlen(letters); i++) {path[pathTop++] = letters[i];//递归，处理下一层数字backTracking(digits, index+1);pathTop--;}
}char ** letterCombinations(char * digits, int* returnSize){//初始化path和resultpath = (char*)malloc(sizeof(char) * strlen(digits));result = (char**)malloc(sizeof(char*) * 300);*returnSize = 0;//若digits数组中元素个数为0，返回空集if(strlen(digits) == 0) return result;pathTop = resultTop = 0;backTracking(digits, 0);*returnSize = resultTop;return result;
}今天难度有点大，慢慢消化吧。
这篇关于Day22.一刷数据结构算法(C语言版) 216组合总和III；17电话号码的字母组合的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！
