本文主要是介绍【算法基础实验】图论-构建无向图,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
构建无向图
前提
JAVA实验环境
理论
无向图的数据结构为邻接表数组,每个数组中保存一个Bag抽象数据类型(Bag类型需要专门讲解)
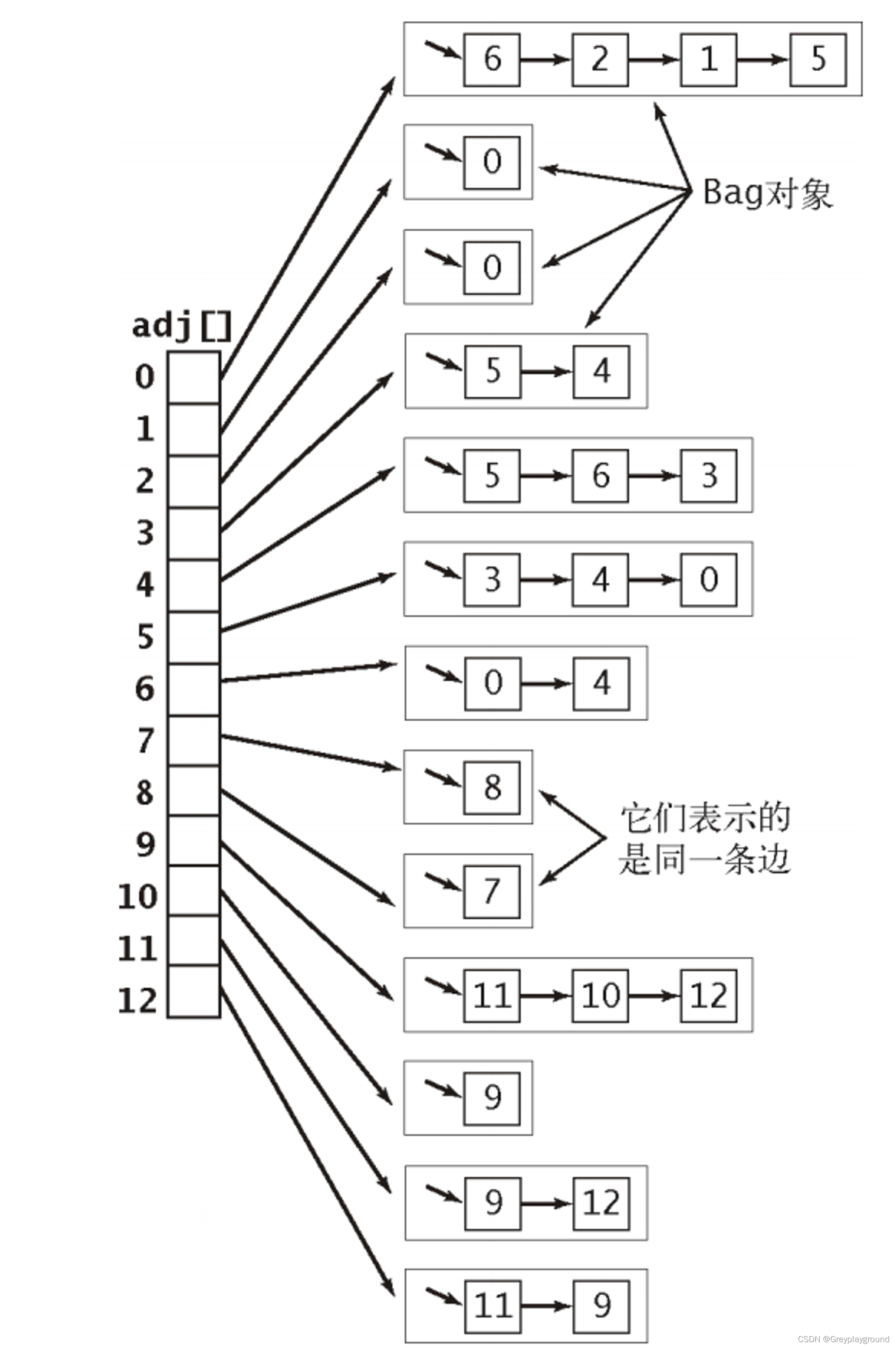
实验数据
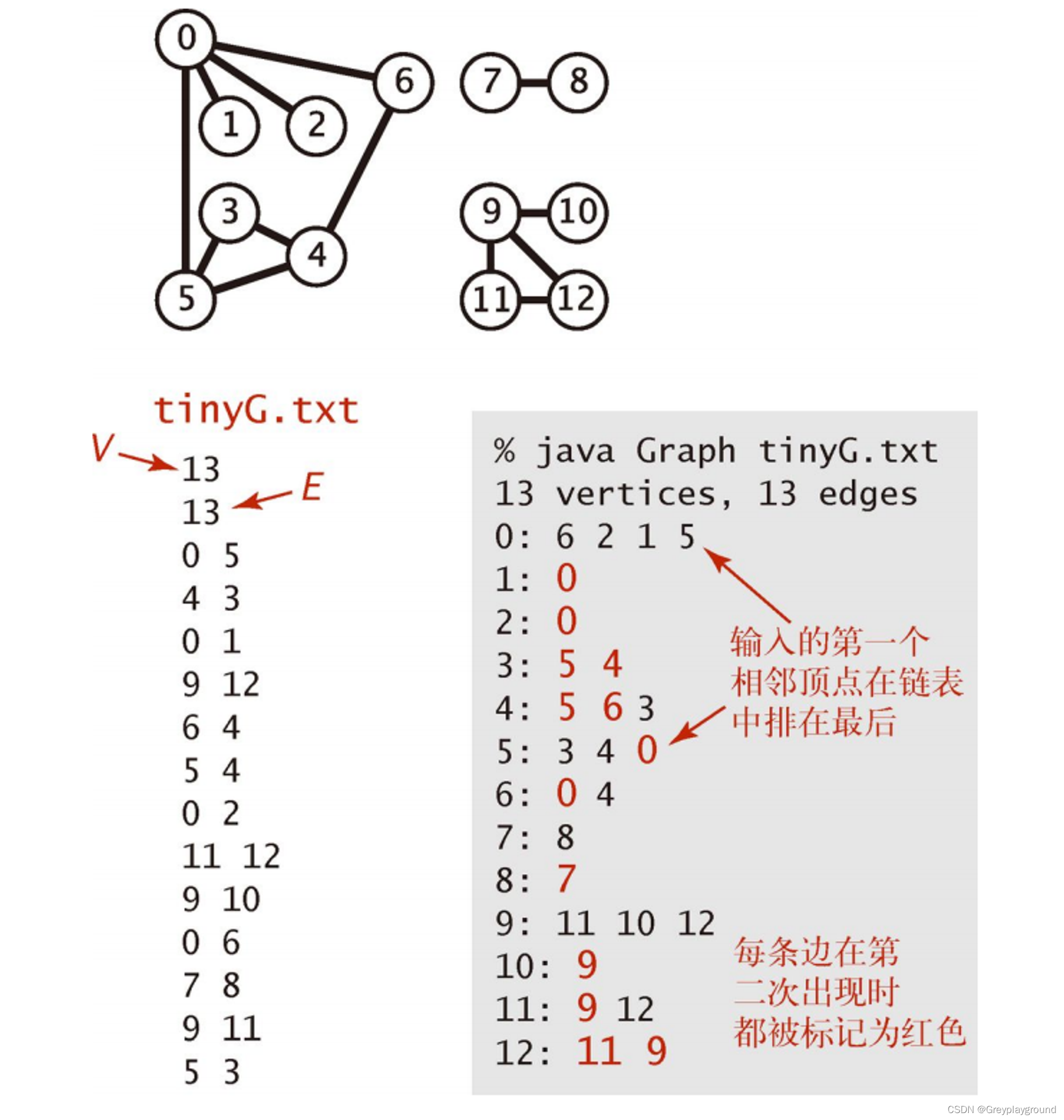
我们的实验数据是13个节点和13条边组成的无向图,由一个txt文件来保存,本实验的目的就是将这个txt文件的图构建出来,并且依次打印出每个节点的所有邻接节点
实验数据下载地址: https://algs4.cs.princeton.edu/code/algs4-data.zip
完整代码
import edu.princeton.cs.algs4.In;
import edu.princeton.cs.algs4.StdOut;public class myGraph
{private final int V;private int E;private myBag<Integer>[] adj;private static final String NEWLINE = System.getProperty("line.separator");public myGraph(int V){this.V = V; this.E = 0;adj = (myBag<Integer>[]) new myBag[V];for (int v = 0; v < V; v++){adj[v] = new myBag<Integer>();}}public myGraph(In in){this(in.readInt());int E = in.readInt();for (int i = 0; i < E; i++){int v = in.readInt();int w = in.readInt();addEdge(v, w);}}public int V() { return V; }public int E() { return E; }public void addEdge(int v, int w){adj[v].add(w);adj[w].add(v);E++;}public Iterable<Integer> adj(int v){ return adj[v]; }public String toString() {StringBuilder s = new StringBuilder();s.append(V + " vertices, " + E + " edges " + NEWLINE);for (int v = 0; v < V; v++) {s.append(v + ": ");for (int w : adj[v]) {s.append(w + " ");}s.append(NEWLINE);}return s.toString();}public static void main(String[] args) {In in = new In(args[0]);myGraph G = new myGraph(in);StdOut.println(G);}
}
代码解读
这段代码是一个用Java编写的图(Graph)数据结构的实现。下面是对这段代码的逐行解读,可以帮助你向其他人详细介绍这个程序:
类定义
public class myGraph
这行定义了一个名为 myGraph 的类,用于表示一个无向图。
成员变量
private final int V; // 图的顶点数
private int E; // 图的边数
private myBag<Integer>[] adj; // 邻接表数组
private static final String NEWLINE = System.getProperty("line.separator"); // 系统换行符
V是图的顶点数,定义为final因为一旦图被创建顶点数是不变的。E是图的边数。adj是一个数组,每个索引处的元素是一个myBag<Integer>类型,用来存储与每个顶点相邻的顶点列表,实现邻接表。NEWLINE是系统相关的换行符,用于输出。
构造方法
public myGraph(int V
这是一个构造方法,接受一个整数 V 作为参数,初始化一个有 V 个顶点但没有边的图。
this.V = V; this.E = 0;
adj = (myBag<Integer>[]) new myBag[V];
for (int v = 0; v < V; v++) {adj[v] = new myBag<Integer>();
}
- 初始化顶点数
V和边数E。 - 创建邻接表数组,每个顶点对应一个新的空
myBag对象。
从输入流构造图
public myGraph(In in)
这个构造方法从输入流 in 构建图。首先读取顶点数和边数,然后读取每一条边的两个顶点,并调用 addEdge 方法添加边。
this(in.readInt()); // 初始化图的顶点
int E = in.readInt(); // 读取边数
for (int i = 0; i < E; i++) {int v = in.readInt(); // 读取一条边的起点int w = in.readInt(); // 读取一条边的终点addEdge(v, w); // 添加边
}
方法定义
public int V() { return V; }
public int E() { return E; }
这两个方法分别返回图的顶点数和边数。
public void addEdge(int v, int w)
此方法用于添加一条连接顶点 v 和 w 的边,并更新邻接表和边数。
adj[v].add(w);
adj[w].add(v);
E++;
- 在顶点
v和w的邻接表中互相添加对方。 - 边数
E自增。
public Iterable<Integer> adj(int v)
{ return adj[v]; }
这个方法返回顶点 v 的邻接顶点列表。
toString 方法
public String toString() {StringBuilder s = new StringBuilder();s.append(V + " vertices, " + E + " edges " + NEWLINE);for (int v = 0; v < V; v++) {s.append(v + ": ");for (int w : adj[v]) {s.append(w + " ");}s.append(NEWLINE);}return s.toString();
}
这个方法返回图的字符串表示形式,包含所有顶点和它们的邻接顶点。
main 方法
public static void main(String[] args) {In in = new In(args[0]);myGraph G = new myGraph(in);StdOut.println(G);
}
main 方法从文件读取图数据,创建 myGraph 实例,并打印图的内容。
这段代码完整地展示了如何在Java中实现一个简单的无向图数据结构,并提供了读取图数据
实验
java myGraph data\tinyG.txt
13 vertices, 13 edges
0: 6 2 1 5
1: 0
2: 0
3: 5 4
4: 5 6 3
5: 3 4 0
6: 0 4
7: 8
8: 7
9: 11 10 12
10: 9
11: 9 12
12: 11 9
参考资料
算法(第4版)人民邮电出版社
这篇关于【算法基础实验】图论-构建无向图的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







