本文主要是介绍轴承寿命预测的基础-对Palmgren理论的再讨论，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！
以下内容为《A.PALMGREN REVISITED--A BASIS FOR BEARING LIFE PREDICTION》的翻译。内容为google翻译，明显错误已进行修改。
概括
轴承技术以及轴承工业随着1850年代自行车的发明而开始发展。与此同时，贝塞麦工艺使高质量钢材成为可能。
1881年，H. Hertz 发表了他的接触应力分析。
到 1902 年，R.Stribeck 发表了他基于赫兹理论的著作，计算了径向负载球轴承的最大负载。
到 1920 年，当今使用的所有滚动轴承类型都已投入生产。 AISI 52100 轴承钢成为这些轴承的首选材料。
从 1918 年开始，工程师们将注意力转向预测这些轴承的寿命。
1924 年，A. Palmgren 发表了一篇论文，概述了他的轴承寿命预测方法。这篇论文是 1947 年发表的 Lundberg-Palmgren 寿命理论的基础。
本文对 1924 年 Palmgren 论文进行了批判性评论，并讨论了其对轴承寿命预测的影响。
介绍
滚动轴承技术至今已经发展了 4000 多年。 HT Morton (1) 在他 1965 年出版的著作《抗摩擦轴承》中描述了滚动轴承技术的演变，我在此进行了总结。到公元一世纪，推力球轴承的先驱已经出现。大约公元 1500 年，L. da Vinci 描述了一种多用途轴承。他还描述了一种枢轴轴承，该枢轴轴承包括一个锥形轴，该锥形轴在三个下部球上枢转，可在角接触座圈中自由旋转。此时，选择的轴承材料是木材和青铜。1556 年，《De Re Metallica》在瑞士出版 (2)。本书介绍了桶泵的滚动轴承并提供了摩擦数据。添加铸铁作为另一种选择的轴承材料。 A. Ramelli 在 1588 年写了一本题为《Le Diverse et Artificiose Machine》的书，其中描述了各种滚动轴承类型。根据 Morton (1) 的说法，下一个重要的发展是 1710 年 de Mondran 的马车，其车轮由滚动轴承支撑。第一个英国滚动轴承专利于 1734 年授予 J. Rowe。大约在公元 1760 年，E. Coulomb 制造了现代球轴承的第一个原型。第一个英国滚珠轴承专利于 1791 年授予 P. Vaughn，用于卡尔车轴。 1802年，M. Cardinet获得了圆锥滚子轴承的法国专利。这些第一批滚动轴承是手工制作的，并且可能是针对特定应用定制的。尽管滚动轴承的创新贯穿了整个 19 世纪上半叶，但直到脚踏自行车的发明，滚动轴承工业才得以建立。 1868年，AC Cowper制造了一辆带有滚珠轴承的自行车，从而使轴承行业一鸣惊人。同年，法国自行车制造商 E. Mishaux凭借一辆配备滚珠轴承的自行车赢得了从巴黎到鲁昂的自行车比赛。根据 Morton (1) 的说法，英国考文垂的 W. Bown 是最成功的轴承制造商。 1880 年，他与自行车制造商 Singer and Company 签订了一份每天生产 12 个滚珠轴承的合同。 Kugelfischer George Schaefer & Co. (FAG)的前身Fischer Bearing Manufacturing, Ltd. 在德国施韦因富特成立，是一家自行车制造商。其创始人 PM Fischer 发明了第一辆踏板自行车。 1883 年，他的儿子 F. Fischer 发明了第一台球磨机。同年，他们开始制造滚珠轴承。铁姆肯公司由 H. Timken 于 1898 年在密苏里州圣路易斯成立，当时是铁姆肯运输公司的子公司。同年，铁姆肯公司开始生产圆锥滚子轴承。 Aktiebolaget Svenska Kullagerfabriken （现为 SKF）由 S. Wingquist于 1907 年在瑞典成立，生产双列自调心球轴承。 Torrington 公司成立于 1866 年，前身是 Excelsior Needle 公司，开始制造滚珠轴承 1912年。许多 其他 轴承公司是 已确立的 期间 这 时间。 到1920 ，大多数类型 使用的滚动轴承的数量 今天 正在生产中。
大约 1875年，碳 和 铬钢开始用于滚动轴承的制造。一个英国人 专利权 颁发给J.Harrington 和 布伦特 1879年 关于 硬化钢衬套 在 一个 内 轴安装 和关于 球。 这种法国钢No.88的化学成分，和美国钢铁公司 和 钢铁研究所(AISI) 规格 52100很接近 。52100在1920年被提出，目前仍然是使用最多的轴承钢。19世纪末， 轴承 行业 开始 到 重点 在 浆纱 轴承 为了 具体应用 和 确定方位 生活 和 可靠性。
1896 年，R.Stribeck(3) 开始对全尺寸轴承进行疲劳测试。1912 年，Goodman 发布了基于疲劳数据的公式，用于计算球轴承和圆柱滚子轴承的安全载荷。 在开发球和滚子轴承寿命预测方法方面最有贡献的人是瑞典人 Arvid Palmgren(5)。 他与 G.Lundberg 教授 (6,7) 的合作成果于 1947 年和 1952 年发表，产生了国际标准化组织 (ISO) 和美国国家标准协会 (ANSI)/抗摩擦轴承制造商协会 (AFBMA) 标准 滚动轴承的额定载荷和寿命 (8-10)。Lundberg-Palmgren 理论和 ISO-ANSI/AFBM 标准的基础在 Palmgren 于 1924 年发表的一篇德国论文中概述。我的目的是 根据我们今天所了解和接受的关于轴承寿命和可靠性的知识，批判性地回顾 1924 年 Palmgren 论文。
伦德伯格-帕尔姆格伦理论
Lundberg-Palmgren 轴承寿命预测理论的起源可以追溯到 1924 年 Palmgren 论文 (11)。然而，由于 1924 年的论文缺少两个要素，因此无法提出全面的轴承寿命理论。
第一个缺失的元素是计算表面下主应力的能力，以及因此计算不合格滚道上的球或滚道上的圆柱滚子的赫兹接触下方的剪切应力的能力。
第二个缺失的要素是符合帕尔姆格伦观察结果的综合生命理论。
正如将要讨论的那样，Palmgren 不信任赫兹理论 (12)，而是依赖于球轴承和滚柱轴承 (11) 的载荷-寿命关系。 1930 年，伊利诺伊大学厄巴纳分校的 V. Thomas 和 H. Hoersch (13) 开发了一种用于确定赫兹接触下的地下主应力的分析方法。 1939 年，W. Weibull (14,15) 发表了他的失败理论。威布尔是帕尔姆格伦的同时代人，并与他分享了自己的工作成果。 Palmgren 与 Lundberg 合作，将他之前的工作与 Weibull 以及 Thomas 和 Hoersch 的工作结合起来，形成了众所周知的 Lundberg-Palmgren 理论 (6,7)。 （Lundberg 和 Palmgren 在他们的论文中没有引用 Thomas 和 Hoersch 的工作。）Lundberg 和 Palmgren (6,7) 使用 Weibull (14,15) 的理论工作，假设概率的倒数的对数生存率 S 可以表示为正交剪切应力 xo、寿命 N、最大正交剪切应力 Zo 的深度和受力体积 V 的幂函数。即，
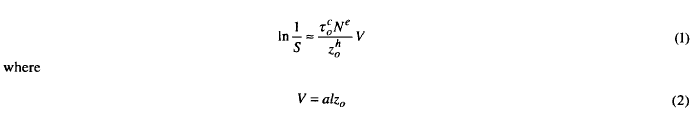
a是赫兹接触椭圆的半长轴， l是滚道的长度。
然后，
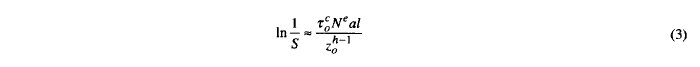
伦德伯格和帕尔格伦的寿命理论基于次表层疲劳。不过，这是我的看法。
根据经验，该理论适用于表面和地下疲劳。 Lundberg 和 Palmgren (6)得到以下附加关系：
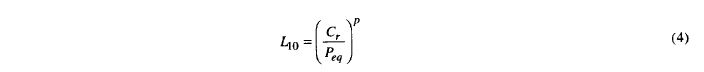其中，C，基本额定动载荷或能力，定义为轴承在内圈旋转 100 万圈且存活概率为 90% 时所能承载的载荷； P eq为轴承当量载荷； p 是负载寿命指数。在 Lundberg-Palmgren (6,7) 的分析中，球轴承使用 p = 3 的值，圆柱滚子轴承使用 p = 10/3 的值。大多数轴承制造商、ANSI/AFBMA（后者现在称为美国轴承制造商协会 (ABMA)）和 ISO 都采用了这些值。将给定载荷和寿命的轴承几何形状和赫兹应力代入方程：对于给定的轴承，(3) 使用适当的指数可得出 C 值。所有后续寿命计算均基于轴承当量载荷Peq 。根据 Lundberg 和 Palmgren (6) 以及 ANSI/ABMA 标准 (9)，球直径小于 25 mm 的向心球轴承的基本额定动载荷为
其中 Cr 是基本额定动载荷，fc 是符合 ANSI/ABMA 标准的轴承几何形状和材料系数， i是滚动元件排数，tr 是轴承接触角，Z 是每排元件数量，d 是球直径。在 Lundberg-Palmgren 寿命方程和 ISO-ANSI/ABMA 标准 (8,9) 中，轴承当量载荷为
其中 Fr 和 Fa 分别是施加到轴承的径向和轴向载荷，X 和 Y 是 Lundberg 和 Palmgren (6) 计算的系数，用于根据 Fa/Fr 比提供适当的等效载荷。对于纯径向载荷， P eq等于 F,。
帕姆格伦关于赫兹压力
Palmgren 对赫兹方程准确预测滚动轴承应力的能力没有信心。 Palmgren (11) 指出，“弯曲表面之间接触时的变形和应力的计算......基于许多简化的规定，这些规定不会产生非常准确的近似值，例如在计算变形时。此外，最近的研究（大约 1919-1923 年）由 A.-B. Svenska Kullager-Fabriken (SKF) 制定，通过计算和实验证明赫兹公式不会产生普遍适用的计算材料应力的程序....由于这个问题对球轴承技术至关重要，SKF 进行了全面的内部研究，以便找到描述因负载、转速、轴承尺寸等变化而引起的使用寿命变化的规律。只有一种可能的方法：对完整的滚珠轴承进行测试，仅进行理论计算是不可接受的，因为滚珠轴承中遇到的实际应力无法通过数学方法确定。”帕尔格伦后来放弃了对赫兹理论有效性的怀疑。 Lundberg 和 Palmgren 在 1947 年的论文 (6) 中指出，“赫兹理论在以下假设下是有效的：与物体的尺寸相比，接触面积很小，并且接触区域中的摩擦力可以忽略不计。对于滚珠轴承，由于滚动元件和滚道之间的紧密一致性，这些条件仅近似正确，对于线接触，只要发生边缘压力，就会超出理论的有效性极限。” Lundberg 和 Palmgren 对修改赫兹理论计算出的合成剪切应力的其他变量表现出了丰富的见解。他们指出（6），“目前还没有人知道材料如何对随后发生的复杂且变化的一系列（剪切）应力做出反应，也没有人知道残余硬化应力的影响或润滑剂如何影响应力赫兹理论也没有考虑环在紧配合安装时因膨胀或压缩而产生的静应力的影响。”现在人们已经了解了这些影响，并且目前正在使用寿命因素来解释这些影响，以便更准确地预测轴承寿命和可靠性 (16)。
当量负载
Palmgren(11) 认识到有必要考虑滚珠轴承圆周周围的组合载荷和可变载荷。他 1924年提出了一项程序 “建立纯径向载荷下轴承使用寿命的函数，并建立将轴向载荷和同时有效的轴向和径向载荷转换为纯径向载荷的规则。” Palmgren 使用 Stribeck's(3) 方程来计算滚珠轴承中最大径向负载滚珠座圈接触处的应力。 Palmgren 归因于 Stribeck 的方程如下：
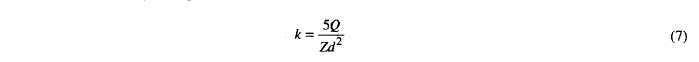
其中Q是轴承上的总径向载荷， Z是轴承中的滚珠数量， d是滚珠直径， k是Stribeck 常数。
Palmgren 修改了 Stribeck 方程，将速度和负载的影响纳入其中，并修改了球直径关系。为了简洁起见，我没有提出这个修改。目前还不清楚 Palmgren 当时是否认识到 Stribeck 方程仅在直径间隙大于零且加载的球少于一半的情况下才有效。然而，他表示修正后的常数与所进行的测试非常吻合。
Palmgren (11) 指出，“可能不可能找到一个准确且简单的表达式来表示球压力作为径向和轴向压力的函数......”根据 Palmgren 的说法，“足够精确的结果可以通过通过使用以下等式获得：
其中Q是想象的纯径向载荷，它将产生与同时作用的径向和轴向力相同的使用寿命， R是实际径向载荷， A是实际轴向载荷。
对于滚珠轴承，Palmgren 将y值表示为 Stribeck 常数 k 的函数。他说这些值已被测试结果所证实，我认为这是他生成的。在 Lundberg-Palmgren (6) 寿命方程和 ISO-ANSI/ABMA 标准 (8,9) 中，方程： (8) 由式(8)代替。 （6）。
在上述所有方程中，我省略了输入变量的单位和 Palmgren 使用的结果单位，因为它们无法合理使用或与当今的工程实践进行比较。因此，这些方程应仅考虑其概念内容，而不应考虑任何定量计算。
疲劳极限
Palmgren (11) 指出，跳动“有限的使用寿命主要是一种疲劳现象。然而，在 异常高的负载还会有其他因素，例如永久变形、直接断裂和 等等......如果我们从材料具有一定疲劳极限的假设开始，这意味着它可以 承受无限数量的循环负载或低于一定的低水平负载，使用寿命曲线 将是渐近的。此外，由于材料具有弹性极限和/或断裂极限，因此曲线必须 即使只有一个负载值，也会产生有限的负载，这意味着周期数为零。 如果我们进一步假设曲线具有指数函数的轮廓，则一般方程为 疲劳前的载荷与载荷循环次数之间存在的关系如下：
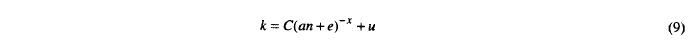
其中k是特定载荷或 Stribeck 常数， C是材料常数， a是载荷循环数 在最大负载暴露点的一转期间， n是以百万为单位的转数， e是材料常数，取决于弹性或断裂极限值， u是疲劳 极限， x是指数。” Palmgren 表示，“这个指数x总是位于 1/3 或 0.3 附近。它的值将接近 1/3 当疲劳极限太高以至于不能忽视时为 0.3，当疲劳极限非常低时为 0.3。” Palmgren 报告 我假设他生成了测试结果，支持x = 1/3 的值。因此，等式。 (9) 可以写成
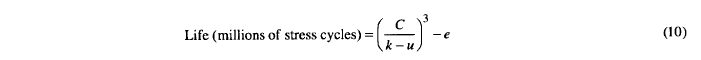
该方程在形式上与方程相似。 (4)，至今仍在使用。当方程。 (4) 发表于 1947 年，Palmgren 与 Lundberg (6) 一起放弃了疲劳极限的概念。 e值表示以下有限时间 预计不会发生任何故障。
通过让e = 0 并消除轴承钢疲劳极限的概念，方程： (10) 可以改写为
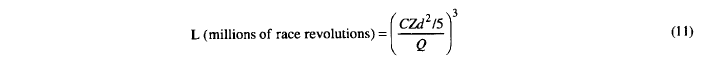
通过让fcm = C/5， Peq = Q,我 = 1，a = 0，1924 年版本的径向球额定动载荷 轴承，当铸造成与方程相同的形式时。 (5), 变为
和等式。 (11) 变为
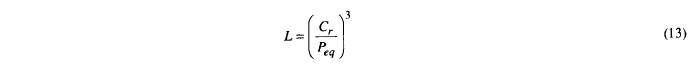等式相同。分别为（5）和（4）。这种相似性表明 Lundberg-Palmgren 方程的起源包含在 1924 年 Palmgren 论文中。
L10寿命
L 1 0 寿命，或一组轴承中 90% 的轴承滚动体不会失效的时间 疲劳，是当今计算轴承寿命和可靠性的基础。接受这一标准意味着 轴承用户原则上愿意接受在此之前轴承组中 10% 会发生故障。在等式 (4)计算出的寿命为L 1 0 寿命。
Palmgren 于 1924 年首次提出了使用 Ll0 寿命的基本原理。他指出 (11)，“（材料）常数 C（方程 (9)）是根据大量运行测试确定的在下面 不同类型的负载。然而，确定这个常数作为一个常数存在一定的困难。 同一轴承类型的不同配置在同等试验下得出的使用寿命结果 状况。因此，有必要说明表达式是否需要最小值、最大值或这两个极端之间的中间使用寿命......为了获得良好的成本 有效的结果，必须接受某些少量轴承的使用寿命会较短 寿命比计算寿命高，因此必须计算常数，以便所有轴承的 90% 剃须刀的使用寿命比公式中规定的要长。必须考虑计算过程 如果我们要记住，从工程和商业的角度来看，这都是完全令人满意的 平均使用寿命比计算使用寿命长得多，并且那些使用寿命较短的轴承 生活实际上只需要通过更换先损坏的部件来进行修理。” 帕尔姆格伦也许是第一个提倡采用概率方法进行工程设计和可靠性的人。当然，当时的工程实践决定了组件设计的确定性方法。 Palmgren 的这种方法领先于时代数十年。 他提倡的是在可接受的风险下实现有限的寿命和可靠性。这一概念已纳入 ISO-ANSI/ABMA 标准 (8-10)，并用于当今的非轴承航空航天设计。
线性损伤规则
大多数轴承在可变负载和速度的组合下运行。 Palmgren 认识到，为了预测轴承寿命，必须考虑负载和速度的变化。 Palmgren 推理道：“为了获得计算值，可以假设轴承
在一定转速（速度）的恒定负载下，其寿命为n万转，其耐用性的一部分m/n将被消耗。如果轴承承受一定的负载并运行mt万转，则其寿命为nl 万转，并在不同的负载下运行m2万转，它将达到n2万转的寿命，依此类推，我们将获得
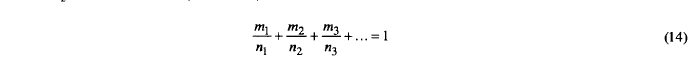
“在循环可变负载的情况下，我们通过引入数量来获得一个方便的公式
间隔p并将m指定为单个间隔内涵盖的百万转数。在这种情况下
我们有
其中n仍然表示在相关负载和转速下的总寿命（以百万转为单位）。”
公式 (14) 是由道格拉斯飞机公司的 Miner (17) 于 1945 年（即 Palmgren 提出后 21 年后）独立提出的，用于常规疲劳分析。该方程随后被称为线性损伤规则或 Palmgren-Miner 规则。为了方便起见，方程可以写成如下：
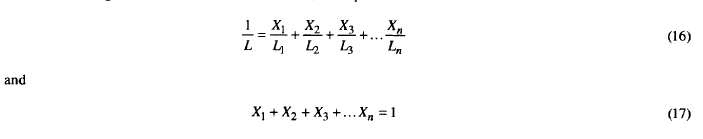
其中L是应力循环或竞赛转数中的总寿命， Lt ...L 是应力循环或竞赛转数中特定负载和速度下的寿命， XI...X是总运行时间的分数负载和速度。该方程是大多数变载荷疲劳分析的基础，并广泛用于轴承寿命预测。
结束语
第一次阅读 Palmgren 论文 (11) 并不一定会给不熟悉轴承寿命预测的读者留下深刻的印象。 Palmgren 在撰写 1924 年论文时有三个目标。这些是“建立纯径向载荷下轴承使用寿命的函数；建立将轴向载荷和同时有效的轴向和径向载荷转换为纯径向载荷的规则；并计算不同类型载荷的影响。随着时间的推移可能会发生变化。”他建立的关系是经验性的。它们基于直觉、实验观察、类比和曲线拟合。他不信任赫兹公式，但仍然在斯特里贝克方程的背景下使用它们。 Palmgren 意识到轴承尺寸是决定轴承寿命的一个因素。然而，我不认为他在 1924 年认识到应力体积对轴承寿命的影响（即，对于给定的应力，较大的轴承寿命会较短）。通过使用 Stribeck 常数（方程（7）），应力体积的影响被无意识地分解到他的方程中，其中包含 d。通过将 Palmgren 方程标准化为早期轴承数据，我认为可以获得合理的寿命预测。
Palmgren 的分析基于轴承座圈的点蚀故障。然而，他确实认识到其他因素会影响轴承的寿命。他首先假设轴承材料具有一定的疲劳极限。然后他质疑是否可以确定这个疲劳极限。他还质疑这种疲劳极限是否如此重要，以至于会对低载荷下运行的轴承产生决定性影响。他接着问道：“如果分析与实验数据一致，是否应该考虑疲劳极限？” Palmgren 回答这些问题时说：“（他的）方程根据多年实际操作中获得的经验规定了某些疲劳极限，这似乎证实实际上必须考虑疲劳极限。”然而，21 年后，在他 1945 年的书 (5) 以及 1947 年与 G. Lundberg (6) 一起，疲劳极限这一概念并未被考虑用于轴承寿命分析。
这篇关于轴承寿命预测的基础-对Palmgren理论的再讨论的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！
