本文主要是介绍磁盘调度算法剖析(FIFO、SSTF、SCAN、CSCAN、FSCAN),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
常见的磁盘调度算法有以下几种:
1.FIFO:先来先服务算法;
2.SSTF: 最短寻道时间算法;
3.SCAN:电梯调度算法;(这样命名很形象)
4.CSCAN: 循环扫描算法
5.FSCAN:分步电梯调度算法(分两个队列)
下面详细说一下各个算法的主要思想:
首先是FIFO算法,也就是先来先服务算法。这种算法的思想比较容易理解。假设当前磁道在某一位置,依次处理服务队列里的每一个磁道,这样做的优点是处理起来比较简单,但缺点是磁头移动的距离和平均移动距离会很大。
其次,是SSTF,最短寻道时间算法。这种算法的本质是利用贪心算法来实现,假设当前磁道在某一位置,接下来处理的是距离当前磁道最近的磁道号,处理完成之后再处理离这个磁道号最近的磁道号,直到所有的磁道号都服务完了程序结束。这样做的优点是性能会优于FIFO算法,但是会产生距离当前磁道较远的磁道号长期得不到服务,也就是“饥饿”现象,因为要求访问的服务的序列号是动态产生的,即各个应用程序可能不断地提出访问不同的磁道号的请求。
接下来,是SCAN算法,也就是很形象的电梯调度算法。先按照一个方向(比如从外向内扫描),扫描的过程中依次访问要求服务的序列。当扫描到最里层的一个服务序列时反向扫描,这里要注意,假设最里层为0号磁道,最里面的一个要求服务的序列是5号,访问完5号之后,就反向了,不需要再往里扫。结合电梯过程更好理解,在电梯往下接人的时候,明知道最下面一层是没有人的,它是不会再往下走的。
然后是,CSCAN算法,循环扫描算法,来看一下上一种算法,有什么问题。仔细一看,我们会发现,在扫描到最里面的要求服务的序列时,接着会反向,在接下来的很大一部分时间里,应该是没有要求服务的磁道号的,因为之前已经访问过了。什么意思,就是说从初始磁道号到最里层的一个磁道号之间的所有序列都已经访问过了,所以SCAN会增加等待的时间。为了解决这样的情况,CSCAN算法的思想是,访问完最里面一个要求服务的序列之后,从最外层的序号开始往里走。也就是始终保持一个方向。就像梳头发,从上往下梳,到了最下面之后,再一次的从上往下梳,这个顺序是不会变的。没有人会从下往上梳头发吧。。
最后,是FSCAN算法,也就是分步电梯调度算法。算法思想是,在扫描的过程中所有新产生的序列放在另外的一个队列中,当访问完当前队列之后,再访问新产生的一个队列。这种算法可以有效防止磁壁粘着现象。
下面结合一个例子来看一下,服务的顺序和计算磁头移动的总距离。
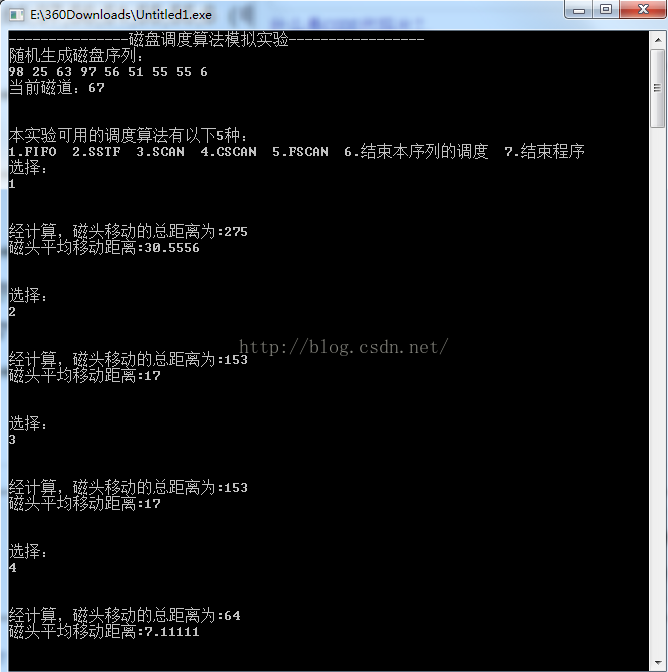
假设当前磁头在67号,要求访问的磁道号顺序为98,25,63,97,56,51,55,55,6 (电脑随机产生的,设定最外层磁道号为100号)
FIFO算法的服务序列是:98,25,63,97,56,51,55,55,6
磁头移动的总距离distance = (98-67)+(98-25)+(63-25)+(97-63)+(97-56)+(56-51)+(55-51)+(55-55)+(55-6)
SSTF算法的服务序列是: 63,56,55,55,51,25,6,97,98
磁头移动的总距离distance = (67-63)+(63-56)+(56-55)+(55-55)+(55-51)+(51-25)+(25-6)+(97-6)+(98-97)
SCAN算法的服务序列是:63,56,55,55,51,25,6,97,98
磁头移动的总距离distance = (67-63)+(63-56)+(56-55)+(55-55)+(55-51)+(51-25)+(25-6)+(97-6)+(98-97)
我发现这里例子举的不好,SSTF和SCAN算法的服务序列竟是一样的,尴尬!
CSCAN算法的服务序列是:63,56,55,55,51,25,6,98,97
磁头移动的总距离distance = (67-63)+(63-56)+(56-55)+(55-55)+(55-51)+(51-25)+(25-6)+(100-98)+(98-97)
上式中,当扫描到磁道6时,直接从6号磁道移动到98号磁道,所以需要计算从6号移动到98号的距离,所以作更正:
distance = (67-63)+(63-56)+(56-55)+(55-55)+(55-51)+(51-25)+(25-6)+|6-98|+(98-97),感谢woshiqinyikun,qq_35819971提出意见
原文地址https://blog.csdn.net/jaster_wisdom/article/details/52345674
这篇关于磁盘调度算法剖析(FIFO、SSTF、SCAN、CSCAN、FSCAN)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!