247.Segment Tree Query II-线段树查询 II（中等题）

本文主要是介绍247.Segment Tree Query II-线段树查询 II（中等题），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

线段树查询 II

1. 题目

   对于一个数组，我们可以对其建立一棵 线段树, 每个结点存储一个额外的值 count 来代表这个结点所指代的数组区间内的元素个数. (数组中并不一定每个位置上都有元素)

   实现一个 query 的方法，该方法接受三个参数 root, start 和 end, 分别代表线段树的根节点和需要查询的区间，找到数组中在区间[start, end]内的元素个数。

2. 样例

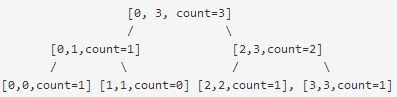
   对于数组 [0, 空，2, 3], 对应的线段树为：
   
   query(1, 1), return 0
   query(1, 2), return 1
   query(2, 3), return 2
   query(0, 2), return 2

3. 挑战

   It is much easier to understand this problem if you finished Segment Tree Buildand Segment Tree Query first.

4. 题解

   和202.Segment Tree Query-线段树的查询（中等题）解题思路一致，唯一不同之处在于本题查询条件会有越界情况出现，如root为[0,4]，而query(2, 5)，所以此处需要特殊处理。

if (root.start >= start && root.end <= end)
{return root.count;
}

/*** Definition of SegmentTreeNode:* public class SegmentTreeNode {*     public int start, end, count;*     public SegmentTreeNode left, right;*     public SegmentTreeNode(int start, int end, int count) {*         this.start = start;*         this.end = end;*         this.count = count;*         this.left = this.right = null;*     }* }*/
public class Solution {/***@param root, start, end: The root of segment tree and *                         an segment / interval*@return: The count number in the interval [start, end]*/public int query(SegmentTreeNode root, int start, int end) {if(start > end || root==null){return 0;}if (root.start >= start && root.end <= end){return root.count;}int mid = (root.start + root.end) / 2;int leftCount = 0;int rightCount = 0;if (mid >= start){leftCount = query(root.left,start,Math.min(mid,end));}if (mid < end){rightCount = query(root.right,mid >= start ? ++mid : start,end);}return leftCount + rightCount;}
}

Last Update 2016.11.5

这篇关于247.Segment Tree Query II-线段树查询 II（中等题）的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---