PCA LDA

本文主要是介绍PCA LDA，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

预备知识

在统计学中，方差是用来度量单个随机变量的离散程度，而协方差则一般用来衡量两个随机变量的联合变化程度。

方差

$${\sigma }_x^2=\frac{1}{n-1}\sum _{i=1}^n{\left(x_i-\bar{x}\right)}^2$$
$n$ 表示样本数量，$\bar{x}$ 表示观测样本的均值。

协方差

$$\sigma (x,y)=\frac{1}{n-1}\sum _{i=1}^n(x_i-\bar{x})(y_i-\bar{y})$$
$\bar{x},\bar{y}$ 分别表示两个随机变量所对应的观测样本均值。方差 ${\sigma }_x^2$ 可看作随机变量 $x$ 关于自身的协方差 $\sigma (x,x)$ 。

协方差矩阵

给定 $d$ 个随机变量 $x_k$ ，$k=1,2,\dots ,d$ 。我们用 $x_{ki}$ 表示随机变量 $x_k$ 中的第 $i$ 个观测样本，每个随机变量所对应的观测样本数量均为 $n$ 。

对于这些随机变量，我们可以根据协方差的定义，求出两两之间的协方差，即：
$$\sigma \left(x_a,x_b\right)=\frac{1}{n-1}\sum _{i=1}^n\left(x_{ai}-{\bar{x}}_a\right)\left(x_{bi}-{\bar{x}}_b\right)$$

因此协方差矩阵为：
$$\Sigma =\left[\begin{array}{ccc}\sigma \left(x_1,x_1\right)& \cdots & \sigma \left(x_1,x_d\right)\\ ⋮& \ddots & ⋮\\ \sigma \left(x_d,x_1\right)& \cdots & \sigma \left(x_d,x_d\right)\end{array}\right]\in {\mathbb{R}}^{d\times d}$$

其中，对角线上的元素为各个随机变量的方差，非对角线上的元素为两两随机变量之间的协方差。

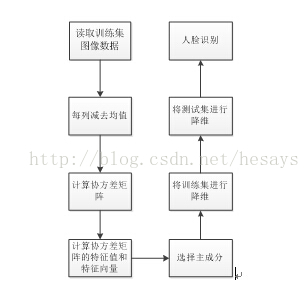
PCA

PCA(主成分分析)是比较常见的线性降维方法，通过线性投影将高维数据映射到低维数据中，所期望的是在投影的维度上，新特征自身的方差尽量大，方差越大特征越有效，尽量使产生的新特征间的相关性越小。

算法流程

假设有 $m$ 条数据，每条数据有 $n$ 个特征。 $x_j^i$ 表示第 $i$ 个样本的第 $j$ 个特征。

1. 均值归一化：
   $$\begin{array}{rl}{\mu }_j& =\frac{1}{m}\sum _{i=1}^m{x}_j^i\\ x_j^i& :=\frac{x_j^i-{\mu }_j}{s_j}\end{array}$$
   其中 $s_j=max(x_j)-min(x_j)$

2. 计算协方差矩阵：
   $$\Sigma =\frac{1}{m}X{X}^T\in {\mathbb{R}}^{n\times n}$$

3. 计算特征向量：
   $$[U,S,V]=svd(\Sigma )$$
   其中左奇异向量、奇异值矩阵、右奇异向量：$U\in {\mathbb{R}}^{n\times n},S\in {\mathbb{R}}^{n\times m},V\in {\mathbb{R}}^{m\times m}$

4. 从 $U$ 中取前 $k$ 列：$U_{reduce}\in {\mathbb{R}}^{n\times k}$

5. 计算得到降维后的数据：$Z=U_{reduce}^T\ast X,Z\in {\mathbb{R}}^{k\times m}$

如何选择 $k$ ？

$$\frac{{\sum }_{i=1}^k{s}_{ii}}{{\sum }_{i=1}^n{s}_{ii}}⩾0.99$$
选择满足上述条件的最小 $k$

降维的应用

• 数据压缩，减少占用的存储空间
• 加快算法计算速度
• 低维平面可以可视化数据

PCA为什么要用协方差矩阵的特征向量矩阵来做投影矩阵呢？

降维的目的就是“降噪”和“去冗余”。

“降噪”的目的就是使保留下来的维度间的相关性尽可能小，而“去冗余”的目的就是使保留下来的维度含有的“能量”即方差尽可能大。

我们要最大化方差来保留更多的信息。去噪。
有趣的是，协方差矩阵能同时表现不同维度间的相关性以及各个维度上的方差。

协方差矩阵度量的是维度与维度之间的关系，而非样本与样本之间。协方差矩阵的主对角线上的元素是各个维度上的方差(即能量)，其他元素是两两维度间的协方差(即相关性)。

先看“降噪”，让保留下的不同维度间的相关性尽可能小，也就是说让协方差矩阵中非对角线元素都基本为零。达到这个目的的方式——矩阵对角化。

再看“去冗余”，对角化后的协方差矩阵，对角线上较小的新方差对应的就是那些该去掉的维度。我们只取那些含有较大能量(特征值)的维度，其余的就舍掉即可。

LDA

LDA(线性判别分析)是一种经典的降维方法。和PCA不考虑样本类别输出的无监督降维技术不同，LDA是一种监督学习的降维技术，数据集的每个样本有类别输出。

LDA分类思想简单总结如下：

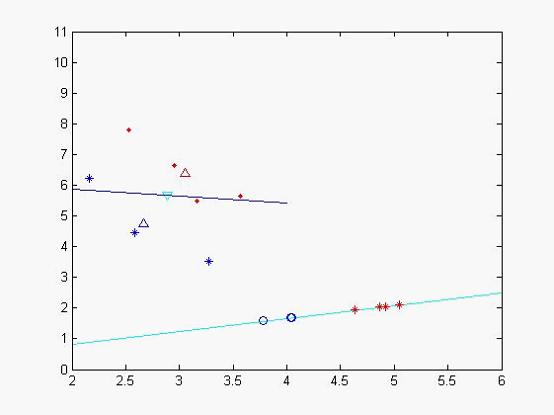
• 多维空间中，数据处理分类问题较为复杂，LDA算法将多维空间中的数据投影到一条直线上，将d维数据转化成1维数据进行处理。
• 对于训练数据，设法将多维数据投影到一条直线上，同类数据的投影点尽可能接近，异类数据点尽可能远离。
• 对数据进行分类时，将其投影到同样的这条直线上，再根据投影点的位置来确定样本的类别。

如果用一句话概括LDA思想：投影后类内方差最小，类间方差最大。

LDA和PCA异同

异同点	LDA	PCA
相同点	1. 两者均可以对数据进行降维； 2. 两者在降维时均使用了矩阵特征分解的思想； 3. 两者都假设数据符合高斯分布；
不同点	有监督	无监督
	降维最多降到 $k-1$ 维	降维多少没有限制
	可以用于降维，还可以用于分类	只用于降维
	选择分类性能最好的投影方向	选择样本点投影具有最大方差的方向
	更明确，更能反映样本间差异	目的较为模糊

---

参考自

• 方差、协方差
• 奇异值分解(SVD)原理与在降维中的应用
• 吴恩达机器学习（十二）主成分分析（降维、PCA）
• 数据分析面试【机器学习】总结之-PCA主成成分分析 常见面试题整理

这篇关于PCA LDA的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---