本文主要是介绍Dilated Convolution膨胀卷积感受野详解,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
重温Dilated Convolution膨胀卷积,对论文《MULTI-SCALE CONTEXT AGGREGATION BY DILATED CONVOLUTIONS》中采用Dilation后的感受野计算示意图产生了迷惑,于是自己重新画图琢磨了一番。

可以看到作者的感受野计算是递进式的,即F1在F0的基础上经3x3,dilation=1卷积得到,即F2在F1的基础上经3x3,dilation=2卷积得到,即F3在F2的基础上经3x3,dilation=4卷积得到,最终F1、F2、F3各自的感受野分别是3x3、7x7、15x15。
这几个数字如果按图示来看无法直观感受到感受野变化的过程,很容易产生迷惑。
在研究变化过程前,需要清楚一个概念,就是每一层的最终感受野是指相对原始图像而言的,在图示中指F0。在清楚这一概念后,则可以开始研究采用dilation后的感受野变化情况。
(1)对原始图F0,采用3x3,dilation=1(即普通卷积)卷积核卷积得到特征图,特征图的每一个单元的感受野则是3x3。这个很好理解。

(2)进一步,对原始图F0,采用3x3,dilation=2卷积核卷积得到特征图,特征图的每一个单元的感受野则是5x5。
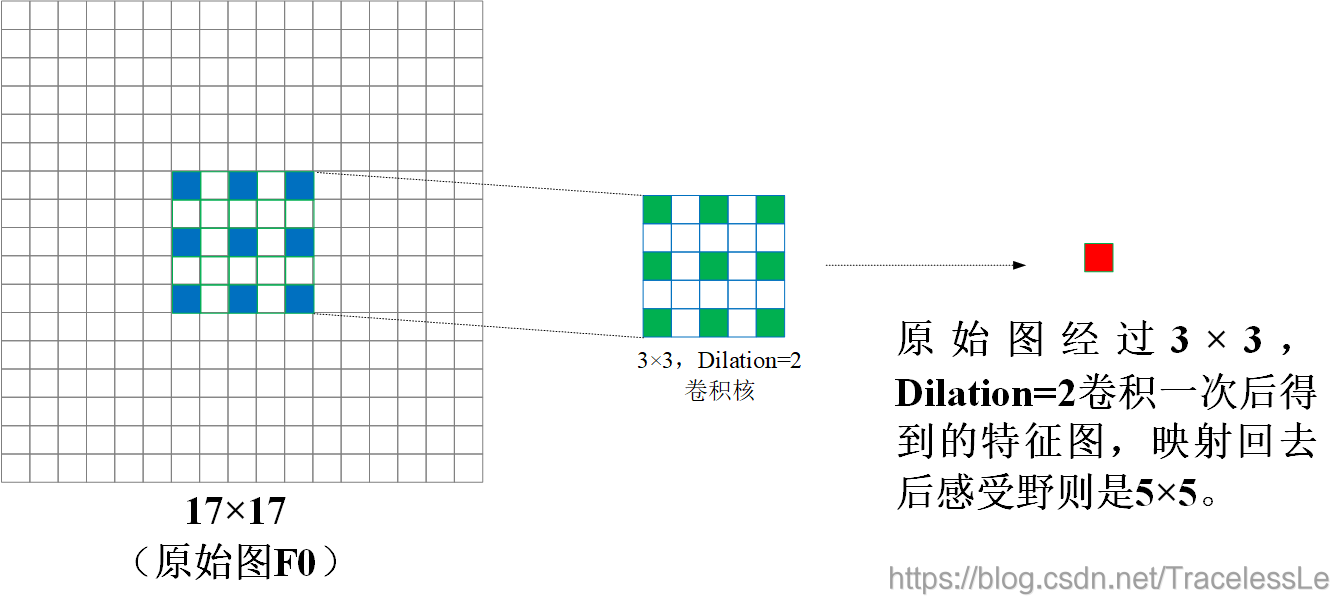
(3)再进一步,对原始图F0,采用3x3,dilation=4卷积核卷积得到特征图,特征图的每一个单元的感受野则是9x9。
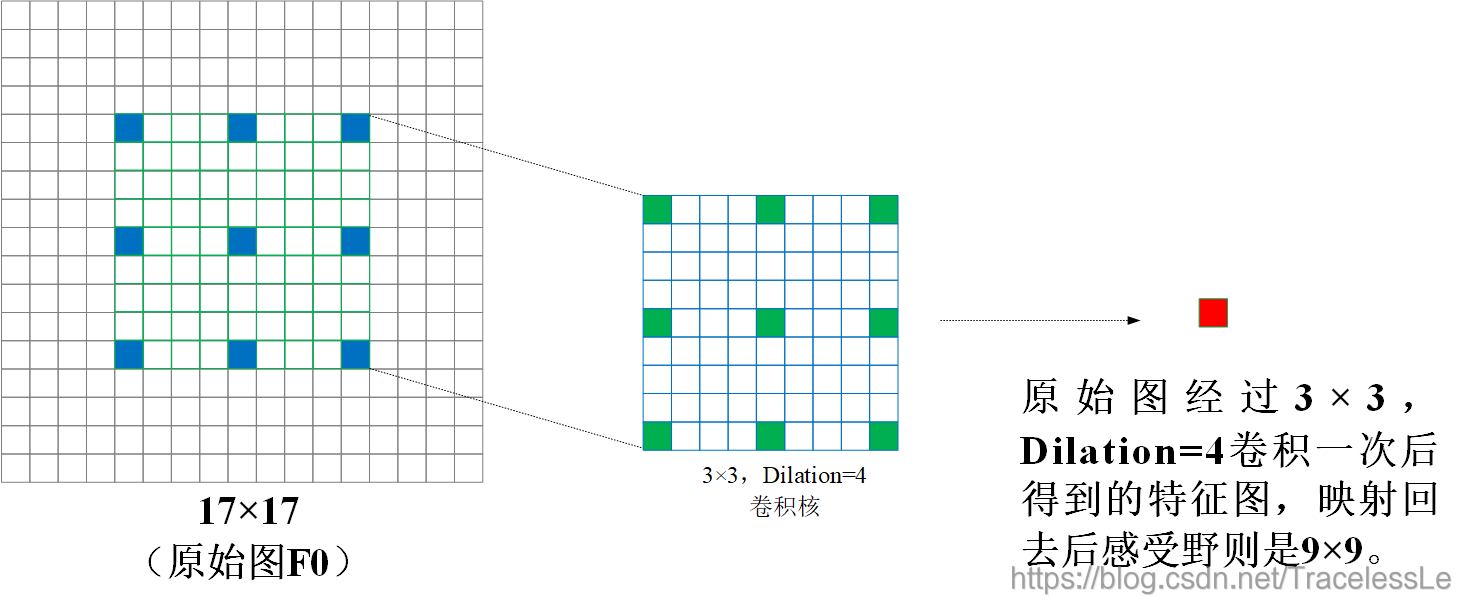
请注意,以上的计算都是卷积直接在原始图F0上进行,因此可以直观看出特征图单个元素对应的感受野。而在原论文中则是递进式的,采用dilation=2/4的卷积核不再是在原始图F0上进行卷积的,这是主要差异。因此感受野计算需要进一步映射。
(4)对原始图F0,先采用3x3,dilation=1(即普通卷积)卷积核卷积得到特征图F1。再采用3x3,dilation=2卷积核卷积得到特征图F2,特征图F2的每一个单元映射回F1后(临时)感受野是5×5,再从F1映射回原始图F0的感受野是[3×3]+(5-1)=[7×7]。则F2每一个单元的最终感受野是7x7,和论文中的F2感受野一致。
注1:(临时)感受野指的是对应前一层特征图的感受野,非对应原始图,不是最终的感受野。
注2:[3×3]是因为F1中的每一个方格对应F0中的3×3个方格,(5-1)是因为需要将3×3卷积核继续平滑4次来生成F1的剩余部分。
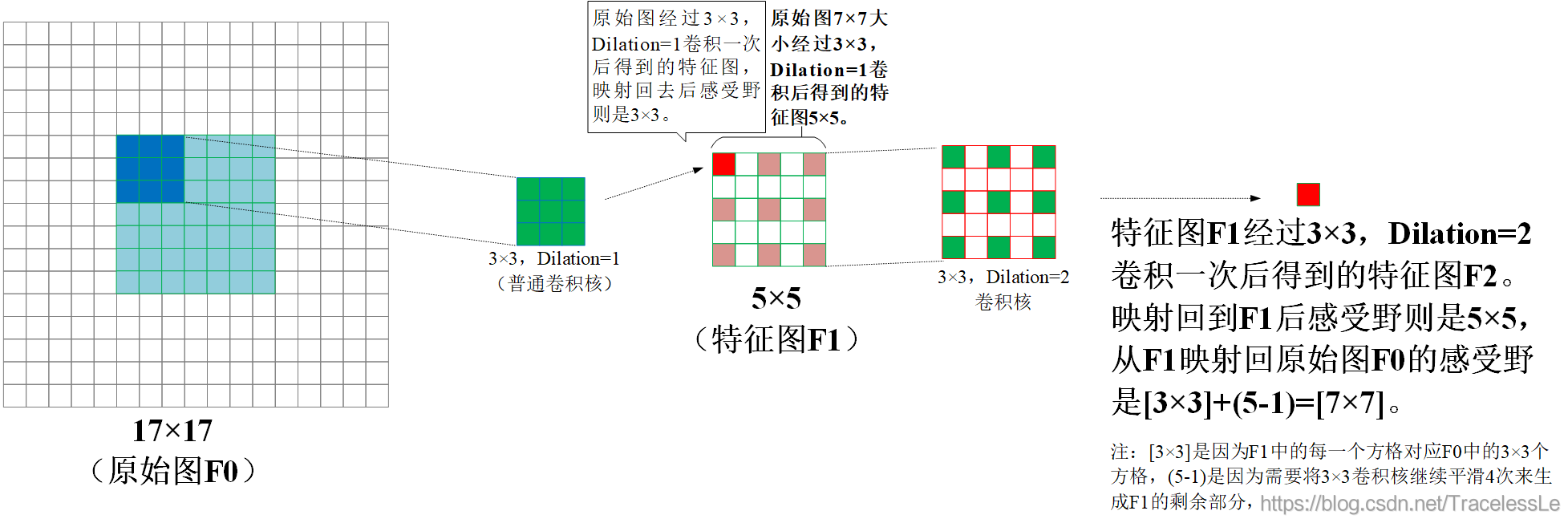
(5)对原始图F0,先采用3x3,dilation=1(即普通卷积)卷积核卷积得到特征图F1。再采用3x3,dilation=2卷积核卷积得到特征图F2,最后采用3x3,dilation=4卷积核卷积得到特征图F3。特征图F3的每一个单元映射回F2后(临时)感受野是9×9,再从F2映射回F1的(临时)感受野是[5×5]+(9-1)=[13×13],最后从F1映射回原始图F0的感受野是[3×3]+(13-1)=[15×15]。则F3每一个单元的最终感受野是15x15,和论文中的F3感受野一致。
注1:(X-1)是因为需要将3×3卷积核继续平滑X-1次来生成特征图的剩余部分,
注2:从F2映射回F1的过程可以直接用F1已映射回F0的感受野来计算,不用再进一步回推。即利用F1对应的原始图感受野[7×7],直接得到F2映射回F0的感受野[7×7]+(9-1)=[15×15]。
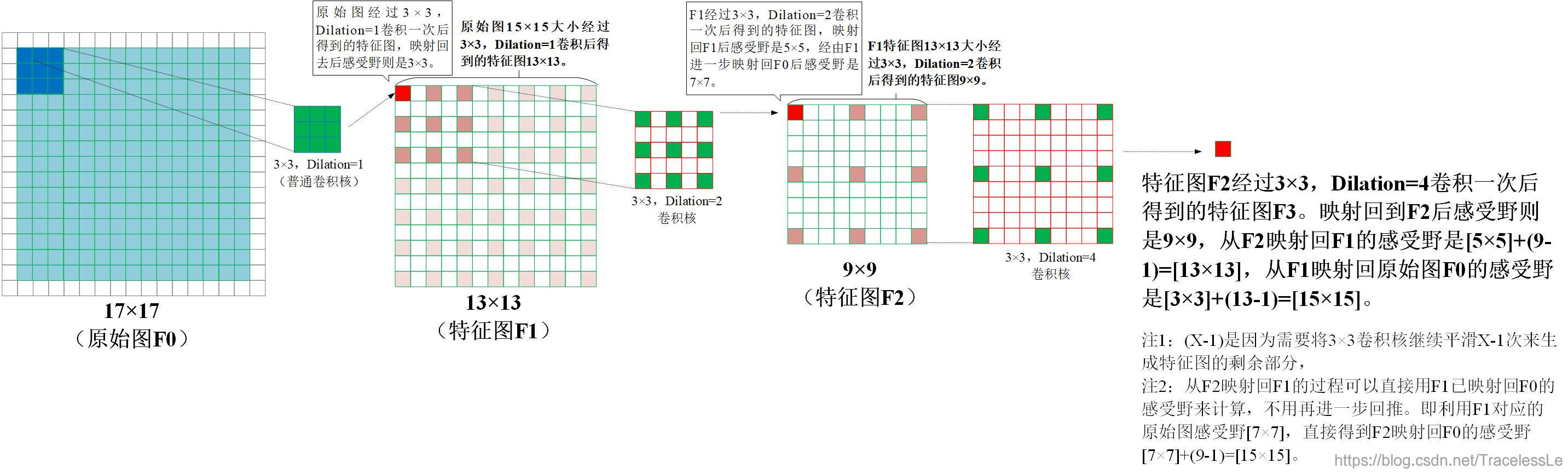
结论:
根据以上图示,能够更加清楚采用Dilated Convolution膨胀卷积后感受野变化的情况,再次强调需要注意的是感受野指的是相对于原始图而言的,因此对于经过多层卷积后得到的特征图的感受野计算,需要层层回退到原始图,最终求得的感受野大小则为所得特征图单个元素的真正感受野。

这篇关于Dilated Convolution膨胀卷积感受野详解的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






