本文主要是介绍动态规划之多阶段决策,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
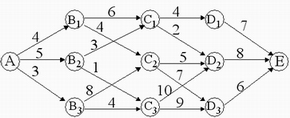
——阶段 动态规划问题通常都具有时间或空间上的次序性,因此求解这类问题时,首先要将问题按一定的次序划分成若干相互联系的阶段,以便能按一定次序去求解。如例1,可以按空间次序划分为A—B—C—D—E 4个阶段,而例2,按照时间次序可分成5个阶段。
阶段变量k
——状态 在多阶段决策过程中,每阶段都需要作出决策,而决策是根据系统所处情况决定的。状态是描述系统情况所必需的信息。如例1中每阶段的出发点位置就是状态,例2中每年初拥有的完好机床数是作出机床负荷安排的根据,所以年初完好机床数是状态。一般地,状态可以用一个变量来描述,称为状态变量。记第k 阶段的状态变量为,k=1,2, …,n.
可达状态集合
决策
最佳策略P
策略
若干个决策按照一定顺序所构成的集合
状态转移方程
在多阶段决策过程中,如果给定了k 阶段的状态变量和决策变量,则第k+1阶段的状态变量也会随之而确定。也就是说是xk和函数,这种关系可记为 =T(xk,uk ) 称之为状态转移方程。
动态规划基本方程
1)全过程的目标函数等于各阶段目标函数的和
fk(Sk)=opt[Vk(Sk,Uk)+fk+1(Sk+1)]
fn+1(Sn+1)=0
2)全过程的目标函数等于各阶段目标函数的积
fk(Sk)=opt[Vk(Sk,Uk)*fk+1(Sk+1)]
fn+1(Sn+1)=1
- 分阶段,确定状态
- 决策变量
- 允许状态集合
- 状态转移方程
5)指标函数——严格单调
6)严格的递归关系
添加链接描述
这篇关于动态规划之多阶段决策的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!



