《算法导论》实验六：红黑树插入算法（C++）——控制台树型显示

本文主要是介绍《算法导论》实验六：红黑树插入算法（C++）——控制台树型显示，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

一、问题描述

我们知道一颗高度为h的二叉搜索树，可以支持任何一种基本动态集合操作，且其时间复杂度均为O(h)。因此，二叉搜索树的性能与树的高度密切相关，如果树的高度较高时，这些集合操作可能并不比在链表上执行得快。所以让树中的元素尽量地平衡在树的两侧，使得树的高度尽量地低，便可提高二叉搜索树的性能。而红黑树（red-black- tree）是许多“平衡的”查找树中的一种，可以保证在最坏情况下基本动态集合操作的时间复杂度为O(lgn)。
因此，为了加强对红黑树的性质及操作的了解，本实验通过编码来实现红黑树的一系列操作（主要是红黑树的插入算法）。

二、算法分析与设计

（一）红黑树的性质如下：
１、每个结点或是红的，或是黑的。
２、根结点是黑的。
３、每个叶结点（NIL）是黑的。
４、如果一个结点是红的，则它的两个儿子都是黑的。
５、对每个结点，从该结点到其子孙的所有路径上包含相同数目的黑结点。

（二）为了实现红黑树插入算法，必须对红黑树的性质有透彻的了解。因为在不断的向红黑树的插入过程中，为了满足“平衡”的优良性质，可能会破坏红黑树的5条性质的某几条，而此时就需要根据5条性质的要求对插入结点及其“附近”结点进行调整。
算法步骤（如下图-1所示）：
Step1：将带插入节点z按BST树规则插入红黑树中，z是叶子节点；
Step2：将z节点涂红；
Step3：调整使其满足红黑树的性质（关键步骤）。


图-1 整个插入算法RBInsert()

（三）调整：
红黑树的插入代码与二叉查找树的插入代码大致相同，区别在于最后z的左右孩子都设为哨兵元素（黑色地NIL），而且z的颜色属性设为红色。新元素插入可能会破坏红黑性质，所以我们要做额外的操作RBInsertFixUp来保持。
Z插入后违反情况：如果它是根结点，则它破坏了性质2：根必须是黑色的。如果它的父亲是红色的，则它破坏了性质4：红结点必须有两个黑色的孩子。对于性质1、3、5，它并不会破坏：它是红色的，满足性质1；它的两个孩子是黑色的T.nil，满足性质3；它是红色的，不会增加黑 高度，满足性质5。
调整步骤：
A、若z为根，将其涂黑；
B、若z为非根，则p[z]存在：
①若p[z]为黑，无需调整
②若p[z]为红，违反性质4，则需调整，且分六种情况进行调整，即父结点是左孩子的三种情况加上父结点是右孩子的三种情况。但后三种情况与前三种情况对称，所以不再赘述，仅以前三种为例：case1：z的叔叔y是红色；case2,：z的叔叔y是黑色，且z是双亲的右孩子；case3：z的叔叔y是黑色，且z是双亲的左孩子。
调整算法如下图-2：

图-2 调整算法RBInsertFixUp()，case4~case6在此略去

三、实验结果与分析

本次实验中，为了能较为全面的覆盖红黑树插入时出现的调整状态，即测试用例能体现插入后不满足性质并且case1、case2和case3的情况都包含进，实验者选择了算法导论（第3版）中的题13.3-2为测试用例来进行试验。
问题13.3-2：将关键字41、38、31、12、19、8连续地插入一颗出初始为空的红黑树后，试画出该结果树？
刚开始程序运行时出现图-3画面，可自由选择实验者想要执行的操作：输入1则表示要插入结点；输入2表示展示红黑树当前状态；输入0表示退出控制台。
因为刚开始红黑树是颗空树，所以选择1进行插入41

图-3 对接下来的操作进行选择

选择1并输入要插入的数41，见下图-4：

图-4 选择1并输入要插入的数41

同理，继续插入38、31，输入操作标记2可树形显示红黑树当前状态：插入31时出现case3，调整颜色并进行一次右旋。见下图-5

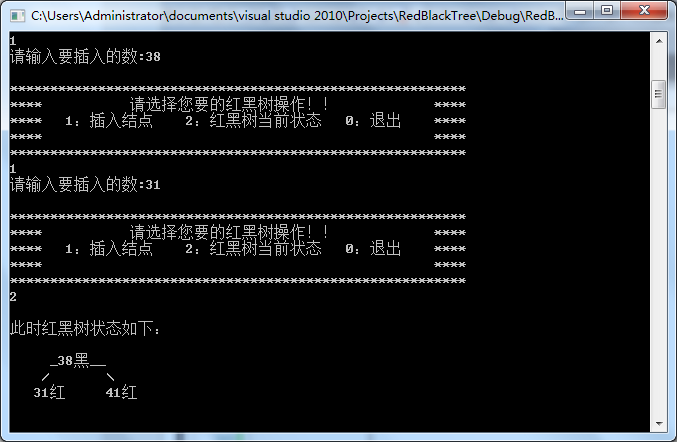
图-5 插入38、31，并树形显示

同理，继续插入12、19，树形显示红黑树当前状态：插入12时出现case1，仅需调整颜色，并且递归向上调整；插入19时出现case2，先左旋，调整颜色后再右旋。见下图-6

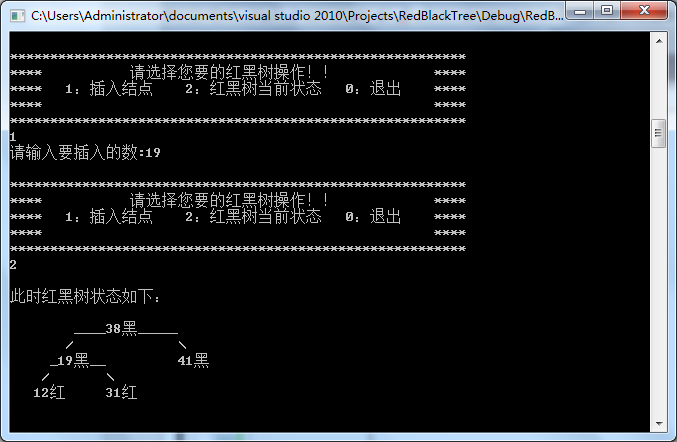
图-6 插入12、19，并树形显示

最后，插入8，树形显示红黑树当前状态：出现case1，仅需调整颜色，并且递归向上调整。

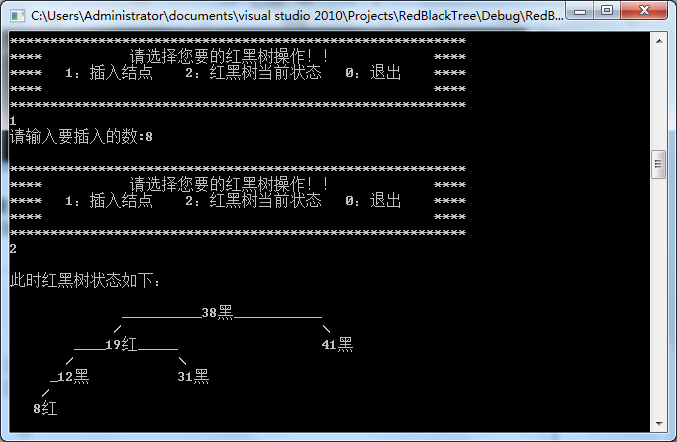
图-7 插入8，树状显示最终结果

四、实验总结

1、 红黑树的是一个“平衡性”很好的二叉搜索树，其基本动态集合操作的时间复杂度为O(lgn)，但在插入时要不断调整以满足红黑树的5条性质。
2、 红黑树插入的过程可能会违反性质2和性质4：当z是根时违反性质2；当z的父母结点是红时违反性质4，因此要做调用函数RBInsertFixUp()进行相应调整。
3、 在时间复杂度方面：调整算法的时间复杂度为O(logn)；整个插入算法的时间复杂度也为O(logn)；此外，调整算法中至多使用2次旋转。

---

五、源代码（C++）

/* 
性质1： 每个结点是红色或黑色 
性质2： 根结点点是黑色
性质3:  每个叶节点（NIL）是黑的
性质4:  如果一个结点是红的，则它的两个儿子都是黑色
性质5:  对每个结点，从该结点到其子孙结点的所有路径上包含相同数目的黑结点
*/  #include <iostream>
#include <deque>
#include <iomanip>
#include <sstream>
#define SENTINEL -100000     //哨兵，作为nil结点的key，方便树状输出时临界点判断
using namespace std;enum Color{RED=0,BLACK=1};   //定义枚举类型，即红黑树结点颜色类型，0表示红色，1表示黑色typedef struct Node          //声明红黑树结点
{Color color;             //红黑树结点的颜色类型,struct Node *parent;     //父节点struct Node *left;       //左孩子struct Node *right;      //右孩子int key;                 //结点键值
}Node;typedef struct RBTree        //定义一个红黑树
{Node *root;              //根节点Node *nil;               //哨兵结点,避免讨论结点的边界情况
}RBTree;void Display()               //选择显示
{cout<<"*********************************************************\n";cout<<"****           请选择您要的红黑树操作！！            ****\n";cout<<"****   1：插入结点    2：红黑树当前状态   0：退出    ****\n";cout<<"****                                                 ****\n";cout<<"*********************************************************\n";
}//左旋，结点x原来的右子树y旋转成x的父母
void LeftRotate(RBTree * rbTree,Node *x)
{if(x->right!=rbTree->nil){Node *y=x->right;x->right=y->left;if(y->left!=rbTree->nil){y

这篇关于《算法导论》实验六：红黑树插入算法（C++）——控制台树型显示的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---