线性代数 | 分开写 |第二章 矩阵及其运算 | 3. 逆矩阵_back

本文主要是介绍线性代数 | 分开写 |第二章 矩阵及其运算 | 3. 逆矩阵_back，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

​​​​​​## .思维导图

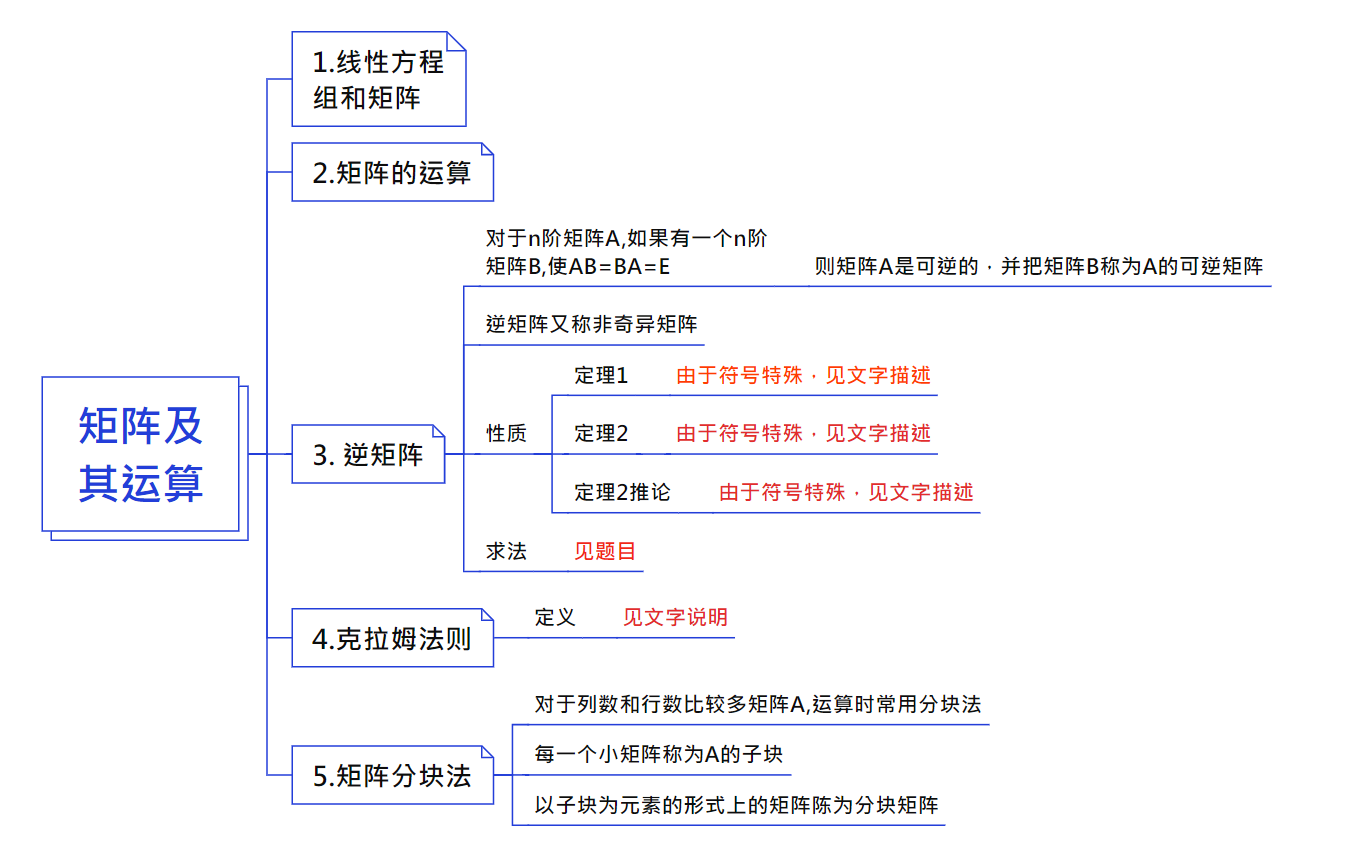
3.1 定义

·定义：设$\mathbf{A},\mathbf{B}$ 是n阶方阵，$\mathbf{E}$ 是n阶单位阵，若 $\mathbf{AB}=\mathbf{BA}=\mathbf{E}$,则称 A 为 可逆矩阵，并称 $\mathbf{B}$ 是 A 的 逆矩阵，并称 $\mathbf{B}$ 是 A 的逆矩阵，且逆矩阵是唯一的，记作 ${\mathbf{A}}^{-1}$。注意逆矩阵是相互的，即有

$$\{\begin{array}{l}{\mathbf{A}}^{-1}=\mathbf{B}\\ {\mathbf{B}}^{-1}=\mathbf{A}\end{array}$$

·$\mathbf{A}$ 可逆的 充要条件 是 $|\mathbf{A}|\ne 0$,当 $|\mathbf{A}|\ne 0$ 时，$\mathbf{A}$ 可逆，且

$${\mathbf{A}}^{-1}=\frac{1}{|\mathbf{A}|}{\mathbf{A}}^{\ast }$$

其中${\mathbf{A}}^{\ast }$ 是矩阵 $\mathbf{A}$ 的伴随矩阵

3.2 性质

性质 1 若矩阵 $A$ 是可逆的，那么 $A$ 的逆矩阵是唯一的。
证明 若$B$、$C$ 都是 $A$ 的逆矩阵，则有

$$B=BE=B(AC)=(BA)C=EC=C$$

所以 $A$ 的逆矩阵是唯一的。

定理 2 若矩阵 $A$ 可逆，则 $|A|\ne 0$ 。

证明 $A$ 可逆，则有$A^{-1}$,使$A{A}^{-1}=E$。故$|A|\cdot |A^{-1}|=|E|=1$,所以 $|A|\ne 0$。
定理3 若$|A|\ne 0$,则矩阵$A$ 可逆，且

A − 1 = 1 ∣ A ∣ A ∗

这篇关于线性代数 | 分开写 |第二章 矩阵及其运算 | 3. 逆矩阵_back的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---