本文主要是介绍MATLAB环境下基于同步压缩变换重分配算子的瞬时频率估计,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
瞬时频率是表征非平稳信号特征的重要物理量,已经被广泛应用于桥梁振动检测、地震勘测、机械、电力系统、雷达、通信、医学等各个方面。瞬时频率的概念最早由Carson提出,后来,Gabor提出解析信号的定义,为瞬时频率的研究提供了新的方向,最后,Ville综合前人研究成果,给出了基于解析信号的瞬时频率的概念,即利用Hilebrt变换得到解析信号,再通过解析信号的相位对时间求导可得信号的瞬时频率。随着时频分析方法的发展,瞬时频率的定义也迎来了新的曙光,在时频分析的层面上,信号在任意时刻的瞬时频率定义为该时刻所有频率的加权平均,即通过计算时频分布的一阶矩即可得信号的瞬时频率。
关于瞬时频率估计的研究非常多,包括相位法、谱峰检测法、过零点法与Teager能量算子法、求根估计法、希尔伯特-黄变换法。总结来讲,两个研究最多的是以下两种瞬时频率估计方法。
(1)基于解析信号的瞬时频率估计法。首先利用Hilebrt变换得待分析信号的
解析信号,再通过解析信号的相位对时间求导可得信号的瞬时频率。
(2)基于时频分布的瞬时频率估计法。首先通过时频分析方法对信号进行变
换得时频分布,再计算该在时频分布的基础上,通过不同的脊线搜索方法可提取出瞬时频率曲线,常用的脊线搜索方法如峰值搜索和Viterbi算法。
在信号的瞬时频率估计问题上,有一点是一直被关注的,即单分量信号和多分量信号在瞬时频率估计过程中的差异,单分量信号,顾名思义,即信号的瞬时频率单一,只有一个瞬时频率值或只有一条瞬时频率曲线,在估计时自然会简单许多。而多分量信号包含了多个瞬时频率信息,多分量之间还可能存在交叉干扰,这些都会大大增加瞬时频率估计的难度。很多方法只适用于单分量信号的瞬时频率估计,在处理多分量信号时便不再奏效。如解析信号法,就需要将多分量信号转化为单分量信号之后再进行瞬时频率估计。而一些时频分析方法也是只能在一定条件下才可用于多分量信号的瞬时频率估计。
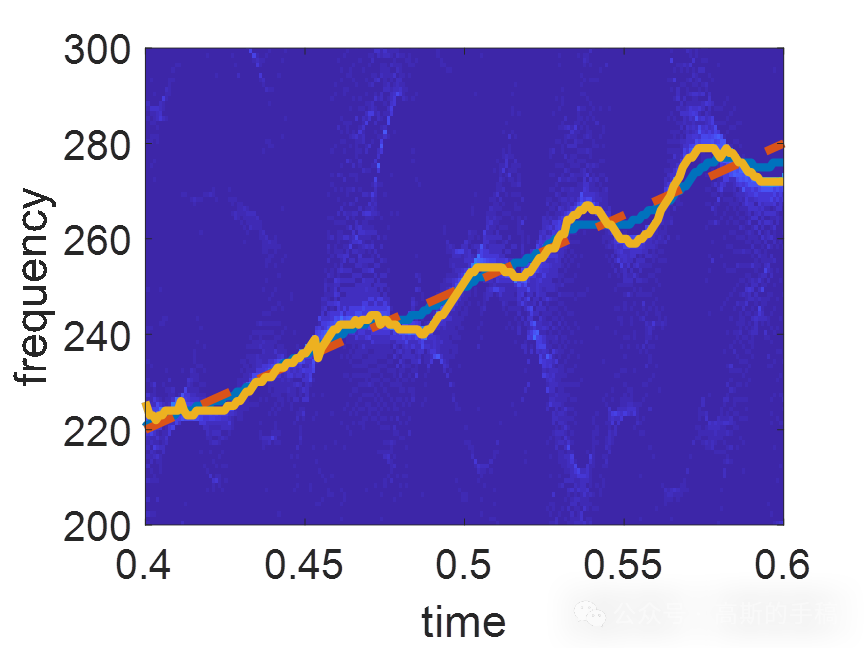
鉴于此,采用同步压缩变换重分配算子对信号的瞬时频率进行估计,运行环境为MATLAB R2018A。
% Window definitiont = -0.5:1/n:0.5-1/n;t=t';g = 1/sigma*exp(-pi/sigma^2*t.^2);gp = -2*pi/sigma^2*t .* g; % g'% InitializationSTFT = zeros(neta,nb);SST1 = zeros(neta,nb);SST2 = zeros(neta,nb);omega = zeros(neta,nb);tau2 = zeros(neta,nb);omega2 = zeros(neta,nb);phi22p = zeros(neta,nb);vg = zeros(neta,7);vgp = zeros(neta,5);
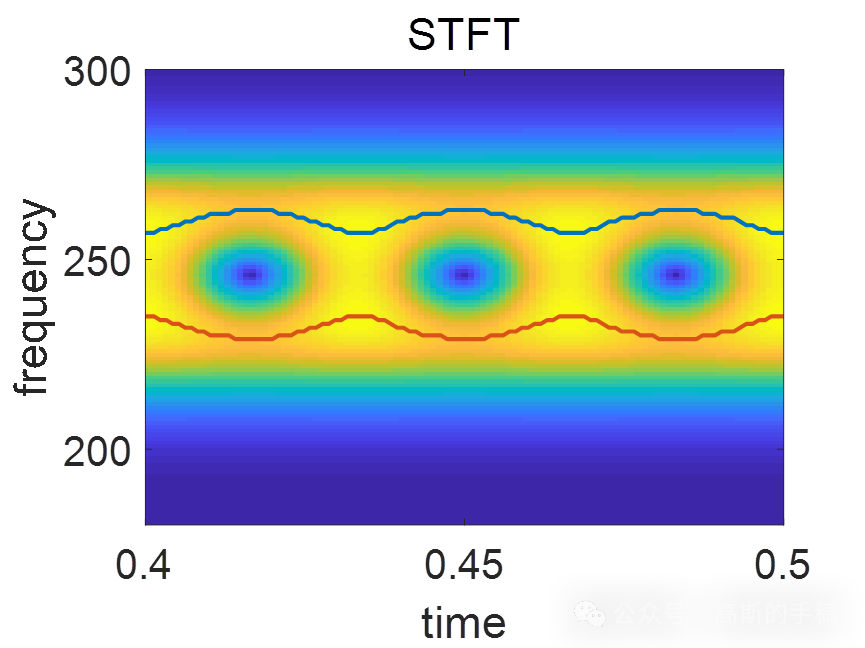
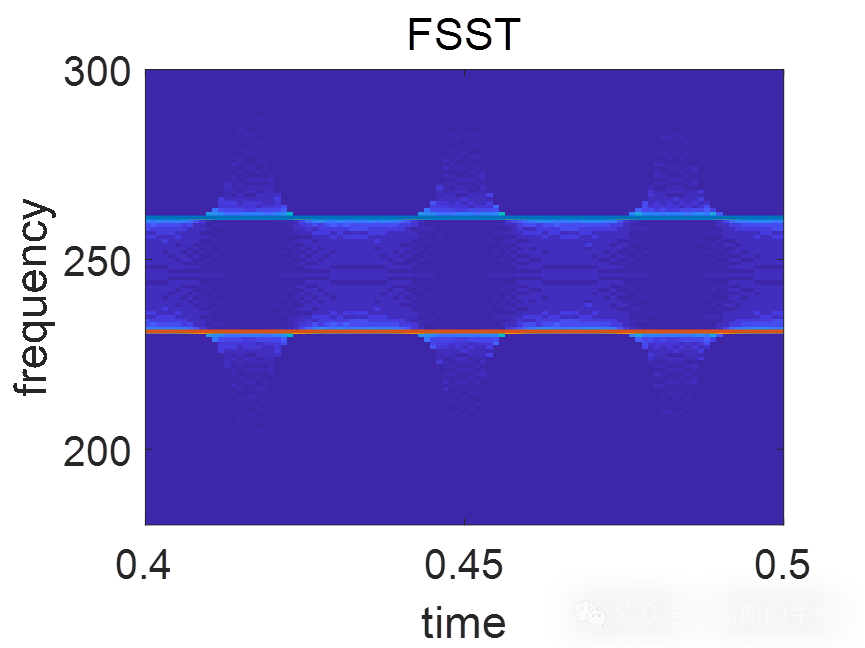
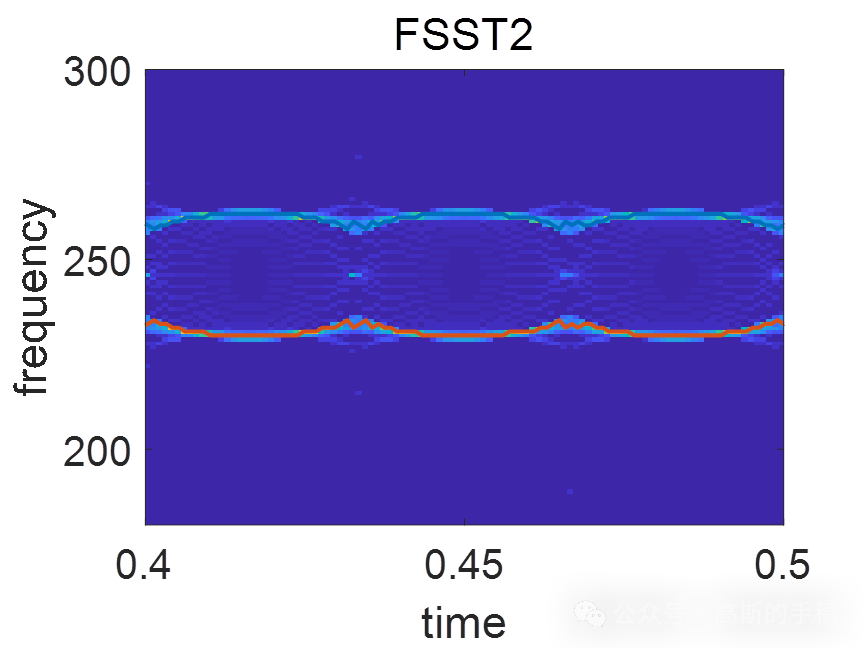
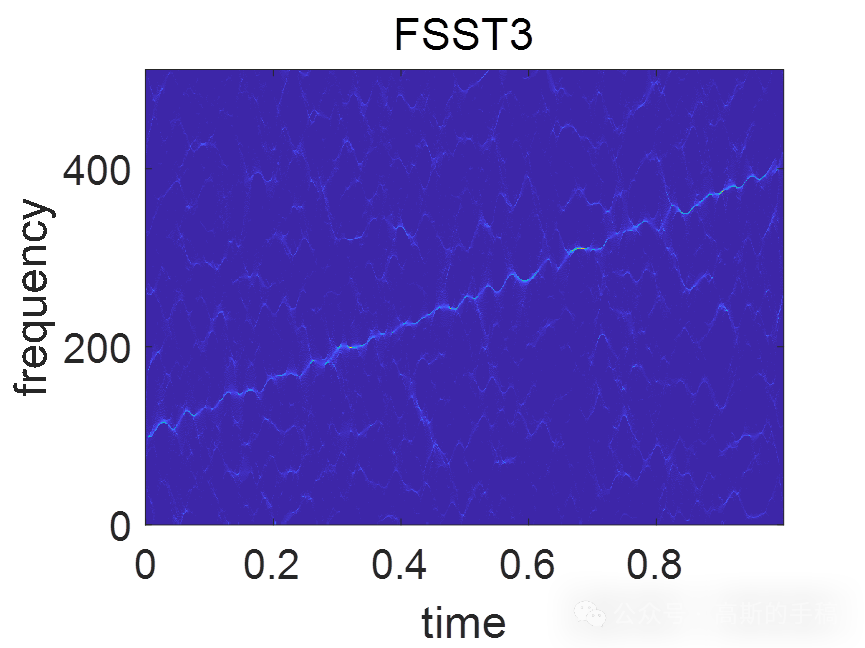
完整代码可通过知乎学术咨询获得:
哥廷根数学学派 - 知乎
工学博士,担任《Mechanical System and Signal Processing》等期刊审稿专家,擅长领域:现代信号处理,机器学习,深度学习,数字孪生,时间序列分析,设备缺陷检测、设备异常检测、设备智能故障诊断与健康管理PHM等。
这篇关于MATLAB环境下基于同步压缩变换重分配算子的瞬时频率估计的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






