【五十四】【算法分析与设计】Manacher算法，Manacher算法作用，Manacher算法流程，Manacher算法证明，Manacher算法代码

本文主要是介绍【五十四】【算法分析与设计】Manacher算法，Manacher算法作用，Manacher算法流程，Manacher算法证明，Manacher算法代码，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

Manacher算法作用

1.

给你一个字符串str，要你求这个字符串的最长回文子串的长度，或者求这个字符串的最长回文子串在str中开始位置的下标。

2.

暴力解法，中心扩散算法，时间复杂度O(N*2)。Manacher算法可以用O(N)解决这个问题。

Manacher字符串

1.

将str转化为ManacherString，例如str="abcd"，那么ManacherString="#a#b#c#d#"。

ManacherString的特点：

• ManacherString中，下标为偶数位置是"#"。

• 偶数下标对应的"#"，下标/2是后面那个字符在str对应的下标。

• 偶数下标对应的"#"，(下标-1)/2是前面那个字符在str对应的下标。

回文半径数组

1.

例如str="aabaca",对应的ManacherString数组="#a#a#b#a#c#a#"。

回文半径数组parr，大小size==ManacherSting.size。MS（ManacherString）一一对应。

2.

对于i=0位置的parr，以i==0为中心，往两边扩展，最长的回文串的长度是多少？显然最长长度是1。

那么parr[i]=1/2+1。表示包括i位置元素在内，往左边或者右边扩展，属于回文串的最长长度。

对于i=1位置的parr，以i==1为中心，往两边扩展，最长的回文串的长度是多少？显然最长长度是3。

那么parr[i]=3/2+1。表示包括i位置元素在内，往左边或者右边扩展，属于回文串的最长长度。

以此类推

3.

对于每一个位置，i表示的是回文串的中心位置。

4.

以i位置为中心，对应的回文直径最左边的下标是i-parr[i]+1，最右边的下标是i+paa[i]-1。注意这个下标是MS中的下标。

5.

每一个回文直径最左边的元素和最右边的元素一定是"#"。

6.

ManacherString的特点：

• ManacherString中，下标为偶数位置是"#"。

• 偶数下标对应的"#"，下标/2是后面那个字符在str对应的下标。

• 偶数下标对应的"#"，(下标-1)/2是前面那个字符在str对应的下标。

• MS中字符如果在原字符串str中存在，下标除以2对应的是再str中的下标。

依靠MS特点找到对应原串str中的回文串区间。

以i位置为例，对应的回文直径最左边的下标是i-parr[i]+1，最右边的下标是i+paa[i]-1。

那么对应str中最左边的下标是(i-parr[i]+1)/2，对应str中最右边的下标是((i+parr[i]-1)-1)/2。

Manacher算法

1.

当我们把所有的MS对应的parr计算完，找到最长回文半径的中心c，对应MS中回文串最左边下标是c-parr[c]+1，对应MS中回文串最右边下标是c+parr[c]-1。

对应str原串中最左边的下标是(c-parr[c]+1)/2，对应str原串中最右边的下标是((c+parr[c]-1)-1)/2。

此时这两个下标就是最长回文串的左右区间。

2.

计算回文半径数组（Manacher算法）。

从左往右开始计算parr[i]，当我们计算i位置的parr[i]时，表示我们已经求出来了parr[0]~parr[i-1]的值。

当然也可以从右往左计算parr[i]，我们只讨论从左往右计算的情况。

3.

定义r表示0~i-1区间中所有位置所能往右扩展的最长回文串右边最远的下标+1位置。

也就是每一个位置最长回文串最右边的下标+1位置。而r记录这个位置最大的值。

定义c表示这个r所对应的回文中心下标。

例如MS="#a#a#b#a"。

i==0时，r=-1，c=-1。

i==1时，r=1，c=0。表示以i=0为中心扩展的回文串区间是[0,0]，r=0+1。

i==2时，r=4，c=1。表示以i=1为中心扩展的回文串区间是[0,3]，r=3+1。所能往右边扩展最远的距离。

i==3时，r=5，c=2。表示以i=2为中心扩展的回文串区间时[0,4]，r=4+1。所能往右边扩展最远的距离。

以此类推。注意并不是最长的回文串对应的r，而是所有位置对应r的最大值。

4.

此时计算i位置的parr[i]，0~i-1parr值都计算完毕。

如果此时i<r。有三种情况。

第一种情况，2*c-i对应的回文串都在[L,R]区间内，并且不压线。2*c-i时i关于c的对称点。以2*c-i为中心对应的最长回文串，如果在[L,R]内，并且不压线，属于第一种情况，此时parr[i]=parr[2*c-i]。

第二种情况，2*c-i对应的回文串不都在[L,R]区间内。此时parr[i]的下界为r-i，即parr[i]=r-i。然后左边下一个待匹配的位置是i-parr[i]（parr[i]==r-i），右边下一个待匹配的位置是i+parr[i]。然后循环匹配i-parr[i]和i+parr[i]，直到不能再扩展，以求parr[i]的值。

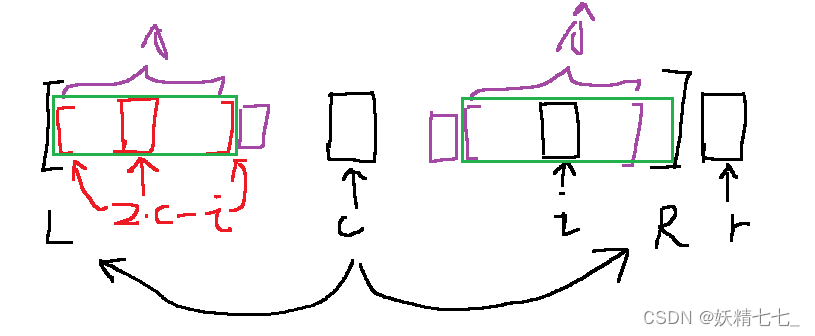
第三种情况，2*c-i对应的回文串都在[L,R]区间内并且压线。此时parr[i]的下界为r-i，即parr[i]=r-i。然后左边下一个待匹配的位置是i-parr[i]（parr[i]==r-i），右边下一个待匹配的位置是i+parr[i]。然后循环匹配i-parr[i]和i+parr[i]，直到不能再扩展，以求parr[i]的值。

如果此时i>=r。此时parr[i]的下界为1。即parr[i]=1。然后左边下一个待匹配的位置是i-parr[i]（parr[i]==r-i），右边下一个待匹配的位置是i+parr[i]。然后循环匹配i-parr[i]和i+parr[i]，直到不能再扩展，以求parr[i]的值。

Manacher算法证明

1.

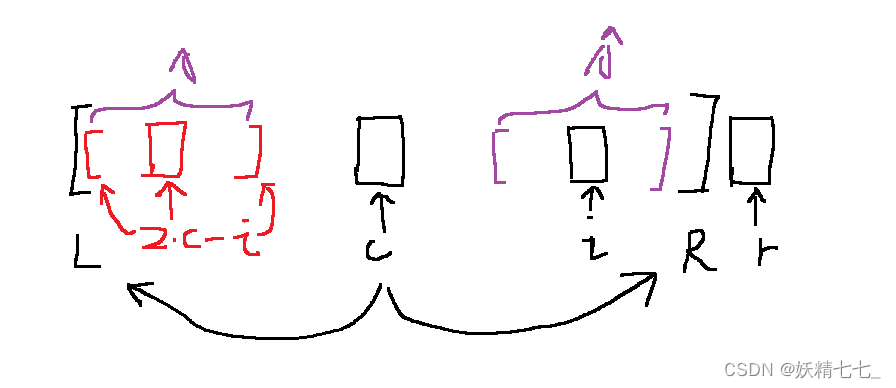
如果此时i<r。有两种情况。

第一种情况，2*c-i对应的回文串都在[L,R]区间内。2*c-i时i关于c的对称点。以2*c-i为中心对应的最长回文串，如果在[L,R]内，属于第一种情况，此时parr[i]=parr[2*c-i]。

A部分与c对称，LR范围是回文串，因此对称过去的字符串是A的逆序。

又因为A字符串是回文串，回文串的逆序是本身。

所以对称过去的字符串与A相等。

a==y,b==x。a!=b,x!=y。因此此时对称过去的区间是以i为中心的最长回文串区间。

2.

第二种情况，2*c-i对应的回文串不都在[L,R]区间内。此时parr[i]的下界为r-i，即parr[i]=r-i。然后左边下一个待匹配的位置是i-parr[i]（parr[i]==r-i），右边下一个待匹配的位置是i+parr[i]。然后循环匹配i-parr[i]和i+parr[i]，直到不能再扩展，以求parr[i]的值。

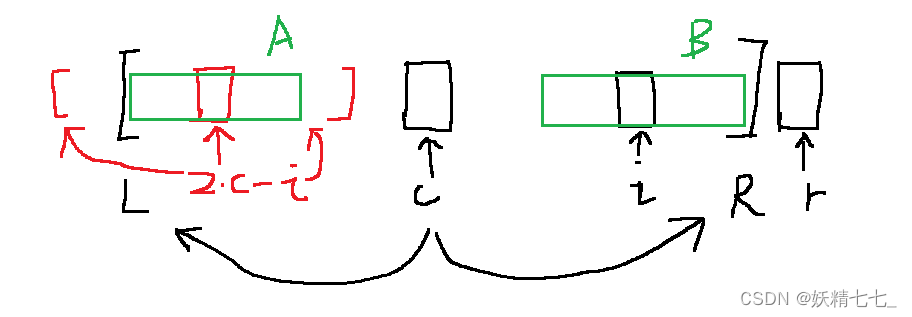
AB关于c对称，AB互为逆序，A本身是回文串，A的逆序等于A本身，因此AB相等。这是以i为中心最长回文串的下界。

左边待匹配位置是i-parr[i]，右边待匹配位置是i+parr[i]，然后不断扩展区间。

3.

第三种情况，2*c-i对应的回文串都在[L,R]区间内并且压线。此时parr[i]的下界为r-i，即parr[i]=r-i。然后左边下一个待匹配的位置是i-parr[i]（parr[i]==r-i），右边下一个待匹配的位置是i+parr[i]。然后循环匹配i-parr[i]和i+parr[i]，直到不能再扩展，以求parr[i]的值。

同理A与对称过去的子串是相同的，此时也是以i为中心最长回文串的下界，到底有多长还不知道，还需要继续扩展。

左边待匹配位置是i-parr[i]，右边待匹配位置是i+parr[i]。不断循环匹配即可。

4.

如果此时i>=r。此时parr[i]的下界为1。即parr[i]=1。然后左边下一个待匹配的位置是i-parr[i]（parr[i]==r-i），右边下一个待匹配的位置是i+parr[i]。然后循环匹配i-parr[i]和i+parr[i]，直到不能再扩展，以求parr[i]的值。

此时以i位置为中心最长回文串长度下界是1，然后左边待匹配下标是i-parr[i]，右边待匹配下标是i+parr[i]。不断循环匹配扩展长度。

Manacher算法代码

代码统一计算以i位置为中心最长回文串的下界，然后统一进行回文串扩展操作，失败就返回，成功就继续。

小结论：MS中最长的回文半径-1等于str最长回文串直径

#include<bits/stdc++.h>
using namespace std;
class ManacherCode {
public:static int manacher(string s) {if (s.size() == 0) return 0;string str = manacherString(s);vector<int> pArr(str.size());int c = -1; int r = -1;int max1 = INT_MIN;for (int i = 0; i < str.size(); i++) {pArr[i] = r > i ? min(pArr[2 * c - i], r - i) : 1;while (i + pArr[i] < str.size() && i - pArr[i] >= 0) {if (str[i - pArr[i]] == str[i + pArr[i]]) {pArr[i]++;} else {break;}}if (i + pArr[i] > r) {r = i + pArr[i];c = i;}max1 = max(max1, pArr[i]);}return max1 - 1;}static string manacherString(string s) {string str(2 * s.size() + 1, '\0');int index = 0;for (int i = 0; i < str.size(); i++) {str[i] = (i & 1) == 0 ? '#' : s[index++];}return str;}
};int main() {string str = { "babad" };cout << ManacherCode().manacher(str);
}

结尾

最后，感谢您阅读我的文章，希望这些内容能够对您有所启发和帮助。如果您有任何问题或想要分享您的观点，请随时在评论区留言。

同时，不要忘记订阅我的博客以获取更多有趣的内容。在未来的文章中，我将继续探讨这个话题的不同方面，为您呈现更多深度和见解。

谢谢您的支持，期待与您在下一篇文章中再次相遇！

这篇关于【五十四】【算法分析与设计】Manacher算法，Manacher算法作用，Manacher算法流程，Manacher算法证明，Manacher算法代码的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---