本文主要是介绍算法学习系列(四十九):最长上升子序列模型(一),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
目录
- 引言
- 一、最长上升子序列
- 二、怪盗基德的滑翔翼
- 三、登山
- 四、合唱队形
- 五、友好城市
- 六、最大上升子序列和
引言
今天学习的是最长上升子序列模型,这种模型我觉得就是我之前说过的就是相当于记忆的过程,记住遇到这种题是用这种模型,下次遇见的时候就能知道了,当然也不完全是死记硬背,相当于是一做了大量的练习,然后考试就可以根据之前做过的大概能知道怎么做,不过考试的时候,基本上就是你能做出来的都是之前有做过类似的题目才行,否则是很难想出来的,也是这个过程就是大量的刷题总结,能从实际问题中抽象出模型或者操作,继续加油吧!
一、最长上升子序列
标签:动态规划、线性DP、最长上升子序列、模板题
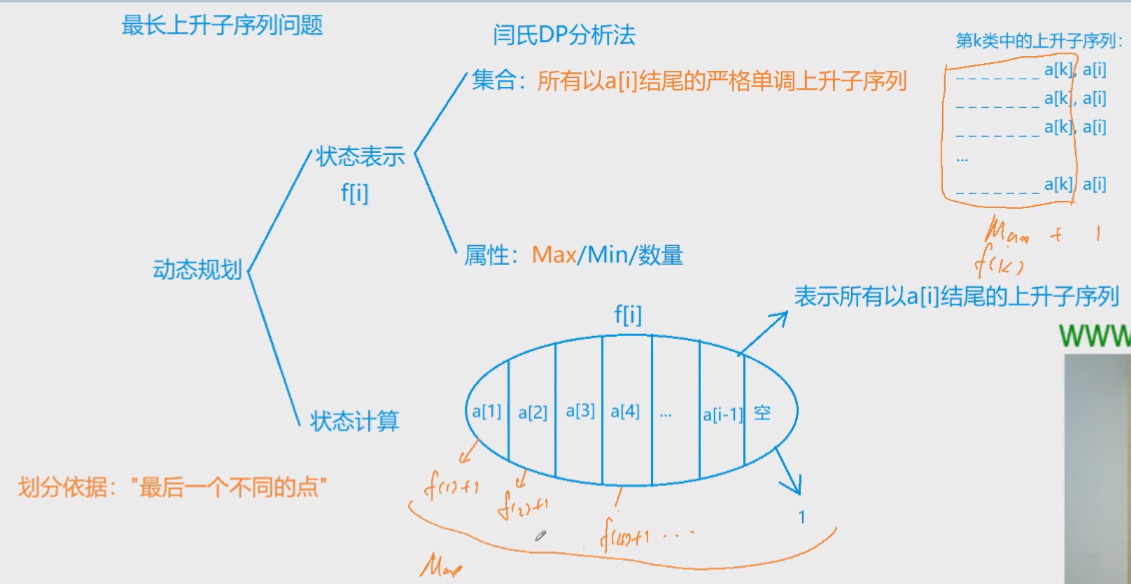
思路:时间复杂度: O ( N 2 ) O(N^2) O(N2) 。首先状态定义: f [ i ] f[i] f[i] 因为是线性的所以,一般都用一维来表示,表示所有以 a [ i ] a[i] a[i] 为结尾的严格单调上升子序列的长度的最大值,然后是状态转移方程(集合划分),通常是以最后一步来划分的,如果说最后一步是 a [ i ] a[i] a[i] ,那么之前的元素可能是从 a [ 1 ] , a [ 2 ] , . . . a [ i − 1 ] a[1],a[2],...\ a[i-1] a[1],a[2],... a[i−1] 中的任意一个元素,当然也可能是空,因为没有一个合法的方案,这时 f [ i ] = 1 f[i] = 1 f[i]=1 然后最大值就是从这些合法的方案中取一个最大值,方程为: f [ i ] = ∑ j = 1 i − 1 m a x ( f [ i ] , f [ j ] + 1 ) , ( a [ i ] > a [ j ] ) f[i] = \sum_{j=1}^{i-1} max(f[i], f[j]+1),(a[i] > a[j]) f[i]=j=1∑i−1max(f[i],f[j]+1),(a[i]>a[j]) 搜索顺序显而易见为线性的从左到右。
题目描述:
给定一个长度为 N 的数列,求数值严格单调递增的子序列的长度最长是多少。输入格式
第一行包含整数 N。第二行包含 N 个整数,表示完整序列。输出格式
输出一个整数,表示最大长度。数据范围
1≤N≤1000,−109≤数列中的数≤109输入样例:
7
3 1 2 1 8 5 6
输出样例:
4
示例代码:
#include <bits/stdc++.h>using namespace std;typedef long long LL;
typedef pair<int,int> PII;
#define x first
#define y secondconst int N = 1010;int n;
int a[N], f[N]; int main()
{ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);cin >> n;for(int i = 1; i <= n; ++i) cin >> a[i];int res = 0;for(int i = 1; i <= n; ++i){f[i] = 1;for(int j = 1; j < i; ++j){if(a[i] > a[j]) f[i] = max(f[i], f[j] + 1);}res = max(res, f[i]);}cout << res << endl;return 0;
}
二、怪盗基德的滑翔翼
标签:DP、线性DP、最长上升子序列
思路:这道题问的其实是从一个高点可以向一个方向去下降,并且一旦方向确定就不能更改,也就是可以看成是从最长上升子序列和最长下降子序列中找最大的值,那其实就跟上一题是一样的了,只不过这道题要求两遍,详情见代码。
题目描述:
怪盗基德是一个充满传奇色彩的怪盗,专门以珠宝为目标的超级盗窃犯。而他最为突出的地方,就是他每次都能逃脱中村警部的重重围堵,而这也很大程度上是多亏了他随身携带的便于操作的滑翔翼。有一天,怪盗基德像往常一样偷走了一颗珍贵的钻石,不料却被柯南小朋友识破了伪装,而他的滑翔翼的动力装置也被柯南踢出
的足球破坏了。不得已,怪盗基德只能操作受损的滑翔翼逃脱。假设城市中一共有N幢建筑排成一条线,每幢建筑的高度各不相同。初始时,怪盗基德可以在任何一幢建筑的顶端。他可以选择一个方向逃跑,但是不能中途改变方向(因为中森警部会在后面追击)。因为滑翔翼动力装置受损,他只能往下滑行(即:只能从较高的建筑滑翔到较低的建筑)。他希望尽可能多地经过不同建筑的顶部,这样可以减缓下降时的冲击力,减少受伤的可能性。请问,他最多可以经过多少幢不同建筑的顶部(包含初始时的建筑)?输入格式
输入数据第一行是一个整数K,代表有K组测试数据。每组测试数据包含两行:第一行是一个整数N,代表有N幢建筑。第二行包含N个不同的整数,每一个对应一幢建筑的高度h,按照
建筑的排列顺序给出。输出格式
对于每一组测试数据,输出一行,包含一个整数,代表怪盗基德最多可以经过的建筑数量。数据范围
1≤K≤100,1≤N≤100,0<h<10000
输入样例:
3
8
300 207 155 299 298 170 158 65
8
65 158 170 298 299 155 207 300
10
2 1 3 4 5 6 7 8 9 10
输出样例:
6
6
9
示例代码:
#include <bits/stdc++.h>using namespace std;typedef long long LL;
typedef pair<int,int> PII;
#define x first
#define y secondconst int N = 110;int n;
int h[N], f[N];int main()
{ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);int T; cin >> T;while(T--){cin >> n;for(int i = 1; i <= n; ++i) cin >> h[i];int res = 0;for(int i = 1; i <= n; ++i){f[i] = 1;for(int j = 1; j < i; ++j){if(h[i] > h[j]) f[i] = max(f[i], f[j] + 1);}res = max(res, f[i]);}for(int i = n; i; --i){f[i] = 1;for(int j = n; j > i; --j){if(h[i] > h[j]) f[i] = max(f[i], f[j] + 1);}res = max(res, f[i]);}cout << res << endl;}return 0;
}
三、登山
标签:DP、线性DP、最长上升子序列
思路:这道题是找到一个先上升再下降的和最大的值,可以直接求一遍最长上升子序列再求一遍最长下降子序列,方程为 r e s = ∑ i = 1 n m a x ( r e s , f [ i ] + g [ i ] − 1 ) res = \sum_{i=1}^{n}max(res, f[i] + g[i] - 1) res=i=1∑nmax(res,f[i]+g[i]−1) f[i],g[i]分别为以h[i]结尾的最长上升/下降子序列最大值 \text{f[i],g[i]分别为以h[i]结尾的最长上升/下降子序列最大值} f[i],g[i]分别为以h[i]结尾的最长上升/下降子序列最大值 其实把这个式子一看就能明白
题目描述:
五一到了,ACM队组织大家去登山观光,队员们发现山上一共有N个景点,并且决定按照顺序来浏览这些景点,即每次所浏览景
点的编号都要大于前一个浏览景点的编号。同时队员们还有另一个登山习惯,就是不连续浏览海拔相同的两个景点,并且一旦开始下山,就不再向上走了。队员们希望在满足上面条件的同时,尽可能多的浏览景点,你能帮他们找出最多可能浏览的景点数么?输入格式
第一行包含整数N,表示景点数量。第二行包含N个整数,表示每个景点的海拔。输出格式
输出一个整数,表示最多能浏览的景点数。数据范围
2≤N≤1000
输入样例:
8
186 186 150 200 160 130 197 220
输出样例:
4
示例代码:
#include <bits/stdc++.h>using namespace std;typedef long long LL;
typedef pair<int,int> PII;
#define x first
#define y secondconst int N = 1010;int n;
int h[N], f[N], g[N];int main()
{ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);cin >> n;for(int i = 1; i <= n; ++i) cin >> h[i];for(int i = 1; i <= n; ++i){f[i] = 1;for(int j = 1; j < i; ++j){if(h[i] > h[j]) f[i] = max(f[i], f[j] + 1);}}for(int i = n; i; --i){g[i] = 1;for(int j = n; j > i; --j){if(h[i] > h[j]) g[i] = max(g[i], g[j] + 1);}}int res = 0;for(int i = 1; i <= n; ++i) res = max(res, f[i] + g[i] - 1);cout << res << endl;return 0;
}
四、合唱队形
标签:DP线性、DP、最长上升子序列、前后缀分解
思路:这道题就是跟上一题基本上是一模一样的,只不过问的是最少需要移除多少位同学,那么就是求满足条件的最大人数,那也就是上一题的答案了,然后用总人数一减就行了。
题目描述:
N 位同学站成一排,音乐老师要请其中的 (N−K) 位同学出列,使得剩下的 K 位同学排成合唱队形。 合唱队形是指这样的一种队形:设 K 位同学从左到右依次编号为 1,2…,K,他们的身高分别为 T1,T2,…,TK, 则他们的
身高满足 T1<…<Ti>Ti+1>…>TK(1≤i≤K)。 你的任务是,已知所有 N 位同学的身高,计算最少需要几位同学出列,可以使得剩下的同学排成合唱队形。输入格式
输入的第一行是一个整数 N,表示同学的总数。第二行有 N 个整数,用空格分隔,第 i 个整数 Ti 是第 i 位同学的身高(厘米)。输出格式
输出包括一行,这一行只包含一个整数,就是最少需要几位同学出列。数据范围
2≤N≤100,130≤Ti≤230
输入样例:
8
186 186 150 200 160 130 197 220
输出样例:
4
示例代码:
#include <bits/stdc++.h>using namespace std;typedef long long LL;
typedef pair<int,int> PII;
#define x first
#define y secondconst int N = 1010;int n;
int h[N], f[N], g[N];int main()
{ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);cin >> n;for(int i = 1; i <= n; ++i) cin >> h[i];for(int i = 1; i <= n; ++i){f[i] = 1;for(int j = 1; j < i; ++j){if(h[i] > h[j]) f[i] = max(f[i], f[j] + 1);}}for(int i = n; i; --i){g[i] = 1;for(int j = n; j > i; --j){if(h[i] > h[j]) g[i] = max(g[i], g[j] + 1);}}int res = 0;for(int i = 1; i <= n; ++i) res = max(res, f[i] + g[i] - 1);cout << n - res << endl;return 0;
}
五、友好城市
标签:DP、线性DP、最长上升子序列
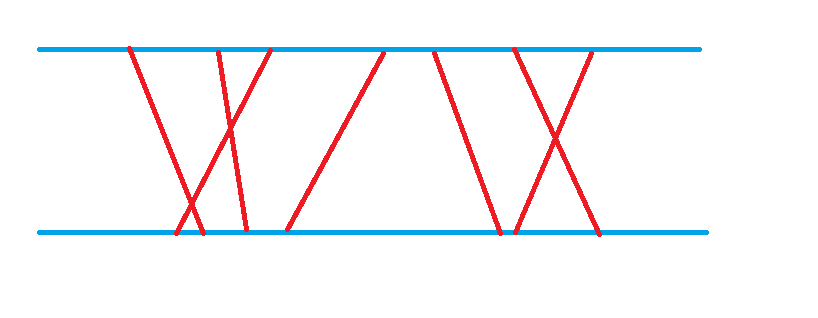
思路:首先这些城市基本上就是如下图的关系,找出其中最多并且不相交的线条,我们发现如果它们不相交的话,那么它们的坐标肯定是单调的,如果我们把上面一端固定住,按照上面城市的坐标顺序看下面的城市,那么如果要不相交,那么其下面的坐标肯定是严格单调上升的。所以先拿 p a i r pair pair 存排个序,然后求其另一个坐标的最长上升子序列,就是我们要求的答案。
题目描述:
Palmia国有一条横贯东西的大河,河有笔直的南北两岸,岸上各有位置各不相同的N个城市。北岸的每个城市有且仅有一个友好城市在南岸,而且不同城市的友好城市不相同。每对友好城市都向政府申请在河上开辟一条直线航道连接两个城市,但是由于河上雾太大,政府决定避免任意两条航道交叉,以
避免事故。编程帮助政府做出一些批准和拒绝申请的决定,使得在保证任意两条航线不相交的情况下,被批准的申请尽量多。输入格式
第1行,一个整数N,表示城市数。第2行到第n+1行,每行两个整数,中间用1个空格隔开,分别表示南岸和北岸的一对友好城市的坐标。输出格式
仅一行,输出一个整数,表示政府所能批准的最多申请数。数据范围
1≤N≤5000,0≤xi≤10000
输入样例:
7
22 4
2 6
10 3
15 12
9 8
17 17
4 2
输出样例:
4
示例代码:
#include <bits/stdc++.h>using namespace std;typedef long long LL;
typedef pair<int,int> PII;
#define x first
#define y secondconst int N = 5010;int n;
int f[N];
PII city[N];int main()
{ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);cin >> n;for(int i = 1; i <= n; ++i) cin >> city[i].x >> city[i].y;sort(city+1, city+1+n);int res = 0;for(int i = 1; i <= n; ++i){f[i] = 1;for(int j = 1; j < i; ++j){if(city[i].y > city[j].y) f[i] = max(f[i], f[j] + 1);}res = max(res, f[i]);}cout << res << endl;return 0;
}
六、最大上升子序列和
标签:DP、线性DP、最长上升子序列
思路:其实本质还是上升子序列,只不过 f [ i ] f[i] f[i] 存的不是长度了,而存的是和的最大值。状态表示: f [ i ] f[i] f[i] 表示以 a [ i ] a[i] a[i] 为结尾的最大上升子序列和,那么上一步可能是 a [ i ] a[i] a[i] 之前的任何一个数,也可能是空值,在这些集合中取最大值。状态转移方程如下: f [ i ] = ∑ j = 1 i − 1 m a x ( f [ i ] , f [ j ] + a [ i ] ) , ( a [ i ] > a [ j ] ) f[i] = \sum_{j=1}^{i-1} max(f[i], f[j]+a[i]),(a[i] > a[j]) f[i]=j=1∑i−1max(f[i],f[j]+a[i]),(a[i]>a[j])
题目描述:
一个数的序列 bi,当 b1<b2<…<bS 的时候,我们称这个序列是上升的。对于给定的一个序列(a1,a2,…,aN),我们可以得到一些上升的子序列(ai1,ai2,…,aiK),这里1≤i1<i2<…<iK≤N。比如,对于序列(1,7,3,5,9,4,8),有它的一些上升子序列,如(1,7),(3,4,8)等等。这些子序列中和最大为18,为子序列(1,3,5,9)的和。你的任务,就是对于给定的序列,求出最大上升子序列和。注意,最长的上升子序列的和不一定是最大的,比如序列(100,1,2,3)的最大上升子序列和为100,而最长上升子序列为(1,2,3)。输入格式
输入的第一行是序列的长度N。第二行给出序列中的N个整数,这些整数的取值范围都在0到10000(可能重复)。输出格式
输出一个整数,表示最大上升子序列和。数据范围
1≤N≤1000
输入样例:
7
1 7 3 5 9 4 8
输出样例:
18
示例代码:
#include <bits/stdc++.h>using namespace std;typedef long long LL;
typedef pair<int,int> PII;
#define x first
#define y secondconst int N = 1010;int n;
int a[N], f[N];int main()
{ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);cin >> n;for(int i = 1; i <= n; ++i) cin >> a[i];int res = 0;for(int i = 1; i <= n; ++i){f[i] = a[i];for(int j = 1; j < i; ++j){if(a[i] > a[j]) f[i] = max(f[i], f[j] + a[i]);}res = max(res, f[i]);}cout << res << endl;return 0;
}
这篇关于算法学习系列(四十九):最长上升子序列模型(一)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







