本文主要是介绍代码随想录第42天 | 01背包问题 二维 、01背包问题 一维 、 416. 分割等和子集,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
一、前言
参考文献:代码随想录
今天很赶,但是又很难!
二、01背包二维问题
1、思路:
自己感觉一开始很抽象,然后理解之后,发现也没有那么抽象;
首先还是dp五部曲;
(1)然后这里的dp数组是二维的:
// 1、定义dp数组vector<vector<int>> dp(nums, vector<int>(bag + 1));/*这里的dp数组i表示物品的标号j表示背包的大小dp[i][j]表示整体总价值*/(2)然后是递推公式,这里还是比较有趣的递推公式:
if (j - weight[i] >= 0) {dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);} else {dp[i][j] = dp[i - 1][j];}如图:
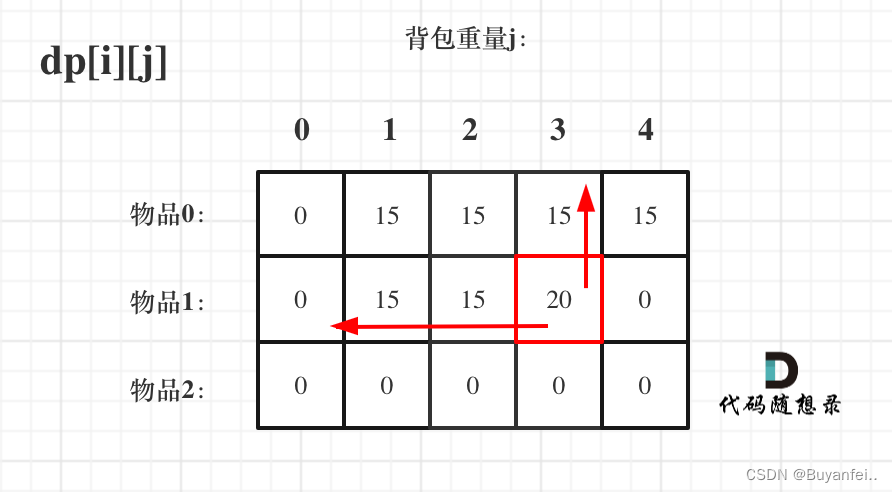
就是通过上面和左上角来推断这个当前装下的最大值 ;
(3)初始化:
/*这里的初始化与不同路径大概差不多,是通过i的weight大小来判断第一列和第一行的总价值大小*/for (int i = 0; i <= bag; i++) {if (weight[0] <= i) {dp[0][i] = value[0];}}接下来的步骤用代码代替了;
2、整体代码如下:
#include<iostream>
#include<vector>using namespace std;int main() {int nums; // 总数量int bag; // 容量cin >> nums >> bag;vector<int> value(nums);// 价值表vector<int> weight(nums); // 重量表// 接收参数for (int i = 0; i < nums; i++) {int j;cin >> j;weight[i] = j;}for (int i = 0; i < nums; i++) {int j;cin >> j;value[i] = j;}// 1、定义dp数组vector<vector<int>> dp(nums, vector<int>(bag + 1));/*这里的dp数组i表示物品的标号j表示背包的大小dp[i][j]表示整体总价值*/// 2、初始化/*这里的初始化与不同路径大概差不多,是通过i的weight大小来判断第一列和第一行的总价值大小*/for (int i = 0; i <= bag; i++) {if (weight[0] <= i) {dp[0][i] = value[0];}}// for (auto i : dp) {// for (auto j : i) {// cout << j << " ";// }// cout << endl;// }// 3、遍历顺序for (int i = 1; i < nums; i++) {for (int j = 1; j <= bag; j++) {// 4、推导公式if (j - weight[i] >= 0) {dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);} else {dp[i][j] = dp[i - 1][j];}}}int result = 0;for (int i = 0; i < nums; i++) {result = max(dp[i][bag], result);}cout << result << endl;return 0;
}三、 01背包问题 一维
1、思路:
时间不够了,明天再补。。。
四、 416. 分割等和子集
1、思路:
这个题目我用二维dp数组做的,主要思想就是把nums[i]的大小为价值又为大小;
然后就是dp五部曲;
2、整体代码如下:
class Solution {
public:bool canPartition(vector<int>& nums) {// 把nums比作物品,然后每个nums对应的数字都是空间// 首先计算出背包有多大int sum = 0;for (int i : nums) {sum += i;}if (sum % 2 != 0) {return false;}int bag = sum / 2;// 1、确定dp数组,及其含义vector<vector<int>> dp(nums.size(), vector<int>(bag + 1));// 在这里的nums是物品,然后所有物品的大小都为1// 2、初始化// 先初始化第一行dp[0][0] = 0;for (int i = 1; i <= bag; i++) {dp[0][i] = nums[0];}// 3、遍历顺序for (int i = 1; i < nums.size(); i++) {for (int j = 1; j <= bag; j++) {if (j >= nums[i]) {dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - nums[i]] + nums[i]);}else {dp[i][j] = dp[i - 1][j];}if (dp[i][j] == bag) {return true;}}}return false;}
};学习时间:2.5小时
The best physicians are Dr. Diet, Dr. Quiet and Dr. Merryman.
最好的医生是规定饮食、安宁和快乐。
这篇关于代码随想录第42天 | 01背包问题 二维 、01背包问题 一维 、 416. 分割等和子集的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





