本文主要是介绍[机器学习必知必会]集成学习Boosting、Boostrap和Bagging算法介绍,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
-
集成学习算法简介:
(1)原理:
集成学习在机器学习算法中具有较高的准去率,不足之处就是模型的训练过程可能比较复杂,效率不是很高。目前接触较多的集成学习主要有2种:基于Boosting的和基于Bagging,前者的代表算法有Adaboost、GBDT、XGBOOST、后者的代表算法主要是随机森林。
集成学习的主要思想是利用一定的手段学习出多个分类器,而且这多个分类器要求是弱分类器,然后将多个分类器进行组合公共预测。核心思想就是如何训练处多个弱分类器以及如何将这些弱分类器进行组合。
(2)算法选择:
一般采用弱分类器的原因在于将误差进行均衡,因为一旦某个分类器太强了就会造成后面的结果受其影响太大,严重的会导致后面的分类器无法进行分类。常用的弱分类器可以采用误差率小于0.5的,比如说逻辑回归、SVM、神经网络。
(3)多个分类器的生成:
可以采用随机选取数据进行分类器的训练,也可以采用不断的调整错误分类的训练数据的权重生成新的分类器。
(4)多个弱分类器的组合
基本分类器之间的整合方式,一般有简单多数投票、权重投票,贝叶斯投票,基于D-S证据理论的整合,基于不同的特征子集的整合。
-
Boosting算法:
(1)Boosting方法是一种用来提高弱分类算法准确度的方法,这种方法通过构造一个预测函数系列,然后以一定的方式将他们组合成一个预测函数。他是一种框架算法,主要是通过对样本集的操作获得样本子集,然后用弱分类算法在样本子集上训练生成一系列的基分类器。他可以用来提高其他弱分类算法的识别率,也就是将其他的弱分类算法作为基分类算法放于Boosting 框架中,通过Boosting框架对训练样本集的操作,得到不同的训练样本子集,用该样本子集去训练生成基分类器;每得到一个样本集就用该基分类算法在该样本集上产生一个基分类器,这样在给定训练轮数n 后,就可产生 n 个基分类器,然后Boosting框架算法将这 n个基分类器进行加权融合,产生一个最后的结果分类器,在这n个基分类器中,每个单个的分类器的识别率不一定很高,但他们联合后的结果有很高的识别率,这样便提高了该弱分类算法的识别率。在产生单个的基分类器时可用相同的分类算法,也可用不同的分类算法,这些算法一般是不稳定的弱分类算法,如神经网络(BP) ,决策树(C4.5)等。
(2)Adaboost
Adaboost是boosting中较为代表的算法,基本思想是通过训练数据的分布构造一个分类器,然后通过误差率求出这个若弱分类器的权重,通过更新训练数据的分布,迭代进行,直到达到迭代次数或者损失函数小于某一阈值。
Adaboost的算法流程:
假设训练数据集为T={(X1,Y1),(X2,Y2),(X3,Y3),(X4,Y4),(X5,Y5)}其中Yi={-1,1}
a、初始化训练数据的分布 :
训练数据的权重分布为D={W11,W12,W13,W14,W15},其中W1i=1/N。即平均分配。
b、选择基本分类器 :
这里选择最简单的线性分类器y=ax+b ,分类器选定之后,最小化分类误差可以求得参数。
c、计算分类器的系数和更新数据权重 :
误差率可以求出来为ei.同时可以求出这个分类器的系数。基本的Adaboost给出的系数计算公式为:,然后更新训练数据的权重分布。
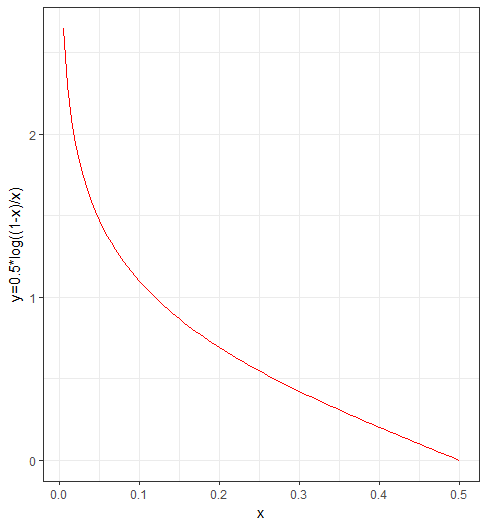
###查看函数形式:
library(ggplot2)
#定义函数
f<-function(x)
{
y<-0.5*log((1-x)/x)
d<-data.frame(x=x,y=y)
return(d)
}
#seq(0,1,0.2) #[1] 0.0 0.2 0.4 0.6 0.8 1.0
#x是误差率,一般0<x<0.5(如果x>0.5则不如直接用随机猜测)
x<-seq(0.005,0.5,0.005)
d<-f(x)
ggplot(d,aes(x,y))+geom_line(color="red")+xlab("x")+ylab("y=0.5*log((1-x)/x)")+theme_bw()
#横坐标是误差率,纵坐标是对应的权重,可以看到随着误差率提高,对应的权重逐渐下降到0。
分类器通过公式组合弱分类器得到。当然这种组合方式基于分类器的系数的,而分类器的系数又是根据误差率求出来的,所以Adaboots最后影响的就是如何使用误差率,以及训练数据更新权重的的计算系数。
注:Adaboost中涉及到的一些可以调整的参数和计算公式的选择主要有以下几点
-
弱分类器如何选择
-
如何更好的根据实验误差率计算分类器的系数
-
如何更好地计算训练数据的权重
-
弱分类器如何组合
-
迭代次数
-
损失函数的阈值选取多少
(3)其他的boosting算法待补充
3、Bagging
bagging方法bootstrap(自助) aggregating的缩写,采用的是随机有放回的选择训练数据然后构造分类器,最后组合。bagging是一种用来提高学习算法准确度的方法,这种方法通过构造一个弱分类器系列,然后以一定的方式将它们组合成一个强分类器。Bagging要求“不稳定”(不稳定是指数据集的小的变动能够使得分类结果的显著的变动)的分类方法。比如:决策树,神经网络算法。
(1)算法原理:
Bagging基于自助采样法(bootstrapsampling)。给定包含M个样本的数据集,先随机取出一个样本放入采样集中,再把该样本放回初始数据集,使得下次采样时该样本仍有可能被选中。这样,经过m次随机采样操作,我们得到含m个样本的采样集,初始训练集中有的样本在采样集里多次出现,有的则从未出现。【即使是同个采样集也有可能存在重复的样本】
采样出T个含有m个训练样本的采样集,然后基于每个采样集训练出一个基学习器,再将这些基本学习器进行结合。
Bagging通常对分了任务使用简单投票法,对回归任务使用简单平均法。
与标准AdaBoost只适用于二分类任务不同,Bagging能不经修改地用于多分类,回归等任务。 自助采样过程还给Bagging带来了另一个优点:由于每个基学习器只使用了初始训练集约63.2%的样本,剩下约36.8%的样本可用作验证集来对泛化性能进行“包外估计”(out-of-bag estimate)。
注:包外估计的用途
当基学习器是决策树时,可使用包外样本来辅助剪枝,或用于估计决策树中各结点的后验概率以辅助对零训练样本结点的处理; 当基学习器是神经网络时,可使用包外样本来辅助早期停止以减小过拟合。
Bagging主要关注降低方差,因此它在不剪枝决策树,神经网络等易受样本扰动的学习器上效用更为明显。【Bagging应用在随机森林和神经网络的原因】【这也正是Bagging要求“不稳定”的原因】
4、boostrap,boosting,bagging几种方法的联系:
(1)Boostrap:名字来源于成语“pull up by your own bootstraps”,即依靠自己的资源,称为自助法,是一种有放回的抽样方法,是非参数统计中一种重要的估计统计量方差进而进行区间估计的统计方法。其核心思想如下:
a、采用有放回的重抽样技术从原始样本中抽取一定数量(自己给定)的样本,此过程允许重复抽样。
b、根据抽出的样本计算给定的统计量T。
c、重复上述过程N次(一般大于1000),得到N个统计量T。
d、计算上述N各统计量T的样本方差,得到统计量的方差。
应该说Bootstrap是现代统计学较为流行的一种统计方法,在小样本时效果很好。通过方差的估计可以构造置信区间等,其运用范围得到进一步延伸。
(2)Bagging:boostrap aggregating的缩写。让该学习算法训练多轮,每轮的训练集由从初始的训练集中随机取出的n个训练样本组成,某个初始训练样本在某轮训练集中可以出现多次或根本不出现,训练之后可得到一个预测函数序列,最终的预测函数H对分类问题采用投票方式,对回归问题采用简单平均方法对新示例进行判别。
【分类器之间其他相同,就是参数不同,所以一般就是随机森林和神经网络】
(3)Boosting:其中最主要的是AdaBoost(Adaptive Boosting)。初始化时对每一个训练例赋予相同的权重1/N,然后用该算法对训练集训练t轮,每次训练后,对训练失败的训练例赋予更大的权重。也就是让学习算法在后续的学习中集中对比较难的训练例进行学习,最后得到一个预测函数序列,其中不同的函数也有一定的权重,预测效果好的预测函数权重较大,反之较小。
(类似Bagging方法,但是训练是串行进行的,第k个分类器训练时关注对前k-1分类器中错分的文档,即不是随机取,而是加大取这些文档的概率。)
(4)Bagging与Boosting的区别:
二者的主要区别是取样方式不同。Bagging采用均匀取样,而Boosting根据错误率来取样,因此Boosting的分类精度要优于Bagging。Bagging的训练集的选择是随机的,各轮训练集之间相互独立,而Boosting的各轮训练集的选择与前面各轮的学习结果有关;Bagging的各个预测函数没有权重,而Boosting是有权重的;Bagging的各个预测函数可以并行生成,而Boosting的各个预测函数只能顺序生成。对于像神经网络这样极为耗时的学习方法。Bagging可通过并行训练节省大量时间开销。
(5)gradient boosting
Gradient Boosting是一种实现Boosting的方法,它主要的思想是,每一次建立模型是在之前建立模型损失函数的梯度下降方向。损失函数(loss function)描述的是模型的不靠谱程度,损失函数越大,则说明模型越容易出错。如果我们的模型能够让损失函数持续的下降,则说明我们的模型在不停的改进,而最好的方式就是让损失函数在其梯度(Gradient)的方向上下降。
(6)Random Forest与Bagging区别:
a、Random Forest是选与输入样本数目相同多的次数(可能一个样本会被选取多次,同时也会造成一些样本不会被选取到),而Bagging一般选取比输入样本的数目少的样本
b、bagging是用全部特征来得到分类器,而random forest是需要从全部特征中选取其中的一部分来训练得到分类器。
c、从而Random Forest效果比Bagging效果好。
5、为什么说bagging是减少variance,而boosting是减少bias
(1)Bagging对样本重采样,对每一重采样得到的子样本集训练一个模型,最后取平均。由于子样本集的相似性以及使用的是同种模型,因此各模型有近似相等的bias和variance(事实上,各模型的分布也近似相同,但不独立)。
由于,理论上若各模型分布相同,则偏差基本不变,但是方差可以显著降低。bagging方法得到的各子模型是有一定相关性的,属于上面两个极端状况的中间态,因此可以一定程度降低variance。为了进一步降低variance,Random forest通过随机选取变量子集做拟合的方式de-correlated了各子模型(树),使得variance进一步降低。
(设有同分布的n个随机变量,方差记为,两两变量之间的相关性为ρ,则的方差为
,bagging降低的是第二项,而Random Forest是同时降低两项)
(2)boosting从优化角度来看,是用forward-stagewise这种贪心法去最小化损失函数。
例如常见的AdaBoost即等价于用这种方法最小化Exponential loss:
所谓的forward-stagewise,就是在迭代的第n步,求解新的子模型f(x)及步长a(或者叫组合系数),来最小化,这里是前n-1步得到的子模型的和。因此boosting是在sequential地最小化损失函数,其bias自然逐步下降。由于采取这种sequential、adaptive的策略,各子模型之间是强相关的,于是子模型之和并不能显著降低方差,所以boosting主要还是靠降低bias来提升预测精度。
这篇关于[机器学习必知必会]集成学习Boosting、Boostrap和Bagging算法介绍的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!