AcWing 206. 石头游戏（矩阵快速幂关于矩阵的一些理解）

本文主要是介绍AcWing 206. 石头游戏（矩阵快速幂关于矩阵的一些理解），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

石头游戏在一个 n 行 m 列 (1≤n,m≤8) 的网格上进行，每个格子对应一种操作序列，操作序列至多有10种，分别用0~9这10个数字指明。

操作序列是一个长度不超过6且循环执行、每秒执行一个字符的字符串。

每秒钟，所有格子同时执行各自操作序列里的下一个字符。

序列中的每个字符是以下格式之一：

1、数字0_{9：表示拿0}9个石头到该格子。
2、NWSE：表示把这个格子内所有的石头推到相邻的格子，N表示上方，W表示左方，S表示下方，E表示右方。
3、D：表示拿走这个格子的所有石头。

给定每种操作序列对应的字符串，以及网格中每个格子对应的操作序列，求石头游戏进行了 t 秒之后，石头最多的格子里有多少个石头。

在游戏开始时，网格是空的。

输入格式
第一行4个整数n, m, t, act。

接下来n行，每行m个字符，表示每个格子对应的操作序列。

最后act行，每行一个字符串，表示从0开始的每个操作序列。

输出格式
一个整数：游戏进行了t秒之后，所有方格中石头最多的格子有多少个石头。

数据范围
1≤m,n≤8,
1≤t≤108,
1≤act≤10
输入样例：
1 6 10 3
011112
1E
E
0
输出样例：
3
样例解释
样例中给出了三组操作序列，第一个格子执行编号为0的操作序列”1E”,第二至五个格子执行编号为1的操作序列”E”,第六个格子执行编号为2的操作序列”0”。

这是另一个类似于传送带的结构，左边的设备0间隔地产生石头并向东传送。

设备1向右传送，直到设备2。

10秒后，总共产生了5个石头，2个在传送带上，3个在最右边。

思路：
思路和代码都是书上的，就不解释了。
简要说一下我对矩阵递推的理解：

假设 $1 * n$ 的矩阵乘上 $x * y$ 的矩阵
那么会出现 $F [i] = \sum F [j] * a [j] [i]$
相当于j,i两个状态间发生了转移。

而对于题目的递推关系就可以用矩阵来表示，矩阵乘法满足结合律，当存在很多相同递推关系时，可以用快速幂的形式加速递推。

再说对于矩阵乘法的理解：
线性代数只是混过了考试，很多概念没有完全理解。
可以参考一下阮一峰的博客
http://www.ruanyifeng.com/blog/2015/09/matrix-multiplication.html

现在对于矩阵乘法的理解是，是一种运算的方法，可以（可以有多种解读）用来表达线性方程组的关系

从方程组
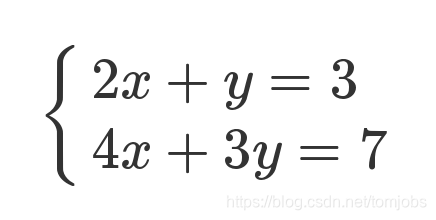
在这里插入图片描述

到了对应的矩阵。
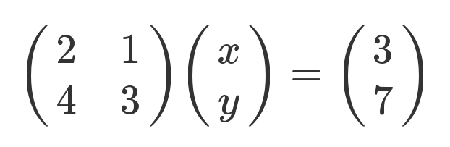
在这里插入图片描述
左边矩阵是 $n * m$ 的
中间的矩阵是 $k * 1 的$

其中 $m = k$ ,这是很自然的，因为未知数必须和系数一一对应。
n则是新矩阵的纵长，代表了有几个方程组。

同理，将中间矩阵扩展宽度q，那么右边矩阵也会扩展相应宽度q。
假设 q = 2
[x a]
[y b]
同样是这个矩阵的每一列与左边矩阵的每一行对应相乘，得到的矩阵中每一列都可以看做一个线性方程组，那么有了q个线性方程组。
就会有 $c [i] [j] = \sum a [i] [k] * b [k] [j]$

如果去掉所谓系数和未知数，统一改为变量，这实际就是一个c[i][j]就是关于a[i][k]和b[k][i]的递推式。

假设有关于x和y的线性方程组
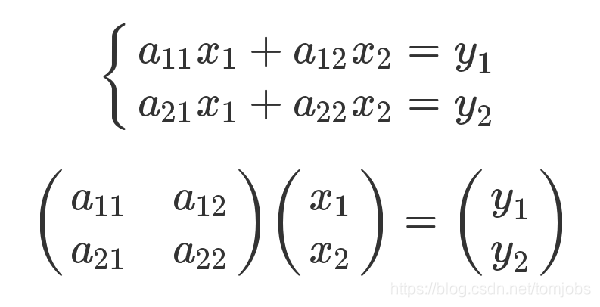
在这里插入图片描述
那么y和x的递推关系为
$y i = \sum x j * a j i$

又有x和t的线性方程组
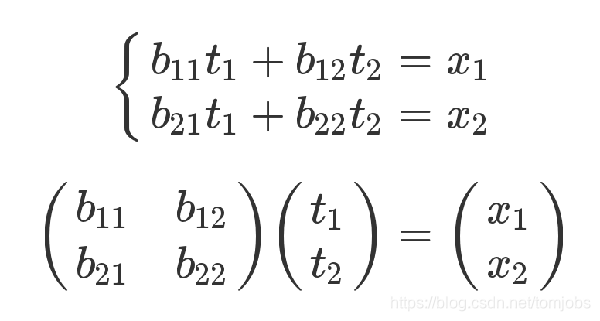
在这里插入图片描述
那么x和t的递推关系为 $x i = \sum t j * b j i$

那么由y和x的递推关系和x和t的递推关系，我们就可以导出
t和y的递推关系
$y i = \sum (\sum t k * b k j) * a j i$

用图表示就是
在这里插入图片描述

前两个矩阵相乘以后为
在这里插入图片描述
很明显符合以上的递推式。

图片均转自阮一峰博客。

#include <cstdio>
#include <cstring>
#include <algorithm>using namespace std;const int maxn = 105;
typedef long long ll;
int n,m,t,act;
int a[maxn][maxn];
ll c[maxn][maxn],e[maxn][maxn][maxn];
ll d[maxn][maxn],f[maxn];
char b[maxn][maxn];
int p;int num(int x,int y)
{return (x - 1) * m + y;
}void mul(ll x[maxn],ll y[maxn][maxn])
{ll z[maxn];memset(z,0,sizeof(z));for(int i = 1;i <= p;i++){for(int j = 1;j <= p;j++){z[i] += x[j] * y[j][i];}}for(int i = 1;i <= p;i++){f[i] = z[i];}
}void mul2(ll x[maxn][maxn],ll y[maxn][maxn])
{ll z[maxn][maxn];memset(z,0,sizeof(z));for(int i = 1;i <= p;i++){for(int j = 1;j <= p;j++){for(int k = 1;k <= p;k++){z[i][j] += x[i][k] * y[k][j];}}}for(int i = 1;i <= p;i++){for(int j = 1;j <= p;j++){x[i][j] = z[i][j];}}
}int main()
{scanf("%d%d%d%d",&n,&m,&t,&act);for(int i = 1;i <= n;i++){for(int j = 1;j <= m;j++){scanf("%1d",&a[i][j]);a[i][j]++;}}for(int i = 1;i <= act;i++){scanf("%s",b[i]);}p = n * m + 1;for(int k = 1;k <= 60;k++){for(int i = 1;i <= n;i++){for(int j = 1;j <= m;j++){int x = a[i][j],y = c[i][j];if(b[x][y] >= '0' && b[x][y] <= '9'){e[k][p][num(i,j)] = b[x][y] - '0';e[k][num(i,j)][num(i,j)] = 1;}else if(b[x][y] == 'N' && i > 1) e[k][num(i,j)][num(i-1,j)] = 1;else if(b[x][y] == 'W' && j > 1)e[k][num(i,j)][num(i,j-1)] = 1;else if(b[x][y] == 'S' && i < n)e[k][num(i,j)][num(i+1,j)] = 1;else if(b[x][y] == 'E' && j < m)e[k][num(i,j)][num(i,j+1)] = 1;c[i][j] = (y + 1) % strlen(b[x]);}}e[k][p][p] = 1;}memcpy(d,e[1],sizeof(e[1]));for(int k = 2;k <= 60;k++){mul2(d,e[k]);}ll ans = 0;f[p] = 1;int w = t / 60;while(w){if(w & 1) mul(f,d);mul2(d,d);w >>= 1;}w = t % 60;for(int i = 1;i <= w;i++) mul(f,e[i]);for(int i = 1;i < p;i++) ans = max(ans,f[i]);printf("%lld\n",ans);return 0;
}