本文主要是介绍【探讨】光场空间结构全维度非线性调控理论及应用,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
摘要:得益于数字全息与几何相位平面光学技术的逐渐成熟,空间结构光场调控及应用研究已在线性光学领域取得蓬勃发展。与之相比,以非线性光学为物理途径的相关研究虽能实现许多关键功能(如光场间信息交互)却仍处于起步阶段。笔者课题组在国家自然科学基金等项目的支持下,近期聚焦光场调控与非线性光学领域前沿问题“空间多模态经典及量子光场的非线性产生、变换及接口技术”,重点突破了空间全维度参量变换理论与相关技术瓶颈,取得了一系列理论及应用创新成果,为高维量子光学相关实验研究的开展打下坚实基础。
关键词:结构光场;非线性光学;光场调控
现代光学的发展始终与人们对光场自由度及相应维度的认知与应用升级保持同步。以操控光场模态结构为目标的光场调控研究也因此成为推动光学理论及应用前沿的核心手段,特别是近30年来对光场空间结构及其高维空间模态的开发与利用,使其逐步成为前沿热点[1−2]。光场调控许多关键功能(诸如光场间信息交互与频率接口操作)的实现都需要以非线性光学为物理手段[3]。因此,非线性光场调控的研究与发展对推动现代光学发展至关重要。非线性光场调控研究当下的核心任务是:探索如何利用光场间、光与物质间的非线性相互作用对目标调控光场在更多维度中(特别是空间模态)实现按需操控;并以新维度为牵引深化非线性光学理论研究,揭示多模态非线性相互作用中的新物理与新效应,推动、发展基于非线性光场调控技术的新概念与新应用。
笔者课题组在国家自然科学基金的支持下,近期聚焦光场调控与非线性光学领域前沿问题“空间多模态经典及量子光场的非线性产生、变换及接口技术”,重点突破了空间全维度参量变换理论与相关技术瓶颈,取得了一系列理论及应用创新成果。
1) 理论创新方面:任意空间结构光场的非线性产生与频率变换为基于空间模态编码的新型高容光通信、高维光学量子信息等应用基础研究提供了重要物理途径。其中,轨道角动量(OAM)模态的参量产生、调控与表征技术已被广泛研究。但OAM以外的冗余空间维度(如径向模态及偏振矢量结构)因非线性变换规律尚不明确,导致在实验研究中无法被重复利用且多被当做噪声维度避而远之,这严重阻碍了通过非线性调控手段对光场完整空间维度的开发与利用。为此,笔者团队系统性突破了相关理论瓶颈:首次给出小信号三波混频中的柱坐标系下空间模态全自由度参量变换理论[4](见图1(a))以及非线性自旋-轨道耦合调制下的参量极化场模型[5](见图1(b))。合并使用上述两项理论工具即可完备描述、预测光场矢量空间结构(振幅、相位及偏振)在任意旁轴二阶参量过程中的非线性传播变化规律[6]。以理论工具为牵引,笔者团队提出非线性像散频率接口技术概念(见图1(c)),并揭示了像散参量过程中新物理效应“反常OAM守恒”,深化了人们对非线性OAM守恒原理的认知[7],相关成果受到国际权威学者团队高度认可并在近期领域综述中多次积极评价[1−3]。
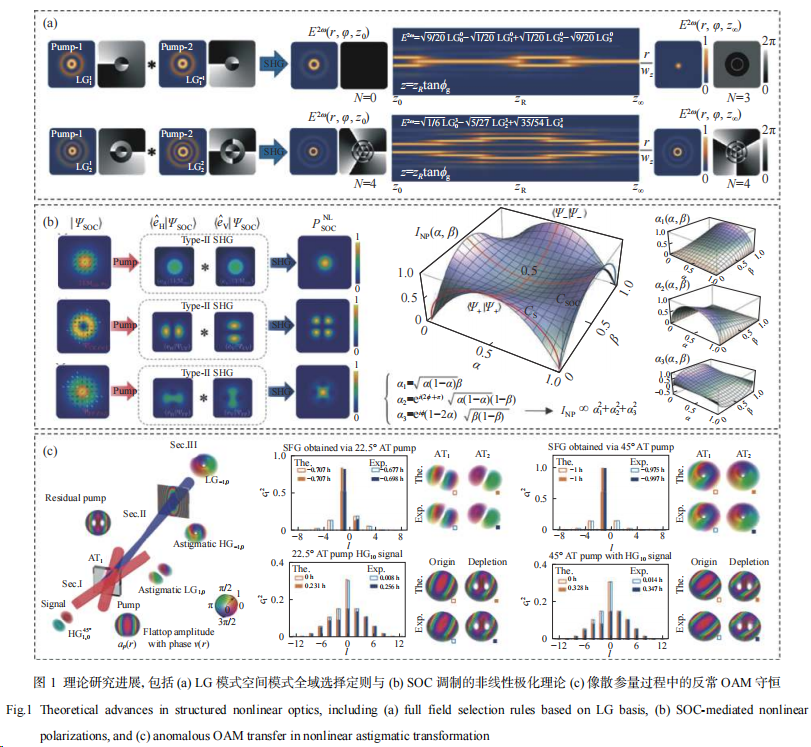
2) 应用创新方面:基于受激参量过程的频率转换是应用最为广泛的非线性光场调控技术之一。其中“频率接口”技术既可实现不同频段信息光场间的交互,还可将红外频率等不便于直接观测的信号转换至硅基探测器的优势探测频段[8]。然而,非线性过程的增益(或量子效率)与相互作用光场的偏振及空间模态相关,这会导致空间模态编码的高维光子态在非线性转换过程中失去原有模态结构。针对这一瓶颈问题,笔者团队以上述理论为指导,提出一种基于超高斯泵浦偏振Sagnac非线性干涉仪的频率变换技术,在国际上首次实现了与信号空间模态及偏振结构无关的保形频率接口[9−10](见图2(a))。该技术可将任意待转换信号的空间模态及所承载的自旋拓扑结构高保真相干传递到新的频率,这一关键技术的突破为面向空间多模态编码的量子接口最终实现奠定重要基础。该光学系统的逆向使用还可实现具有特定空间模态及矢量偏振结构的高维纠缠态制备。在此基础上,通过引入超高斯涡旋泵浦技术,该装置还可在一定范围内实现振幅结构无关OAM频率接口,在不影响信号光场径向动量模态的情况下实现频率与OAM的同步变换[11](见图2(b))。新理论[4]还启发了基于空间多模态非线性光学效应的新应用,笔者团队据此提出一种空间分辨自相关测量技术,首次实现超快光场的时域包络-空间模态联合表征[12](见图2(c))。该技术中的模态间相位信息除用于空间模态识别外,还可用于电场复振幅表征,结合几何相位元件[13]后有望以十分低廉的成本(相较于FROG技术)实现超快光场表征。
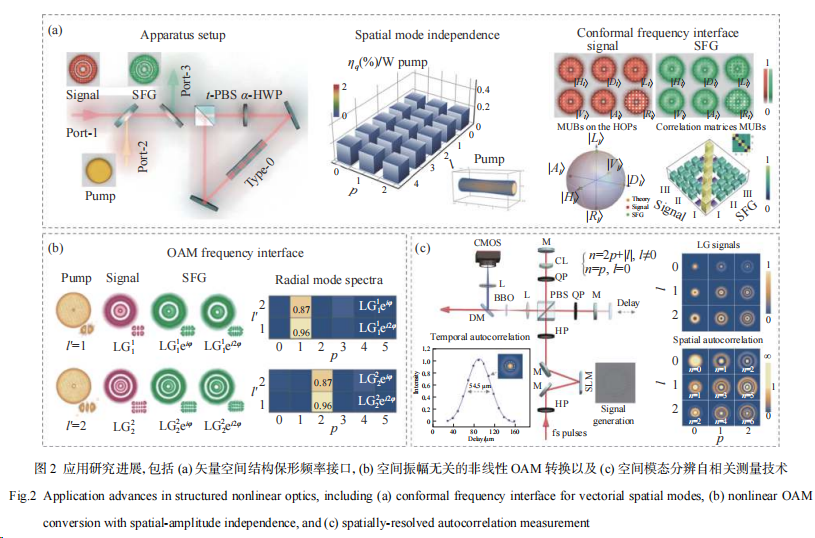
上述系统性研究成果填补了非线空间结构光场全维度调控的关键理论空白,进一步拓展光场调控相关领域的研究思路,对结构激光技术、高维量子态调控、偏振分辨上转换成像等相关研究具有重要指导意义。
参考文献:
[1] Forbes A, de Oliveira M, Dennis M R. Structured light [J]. Nature Photonics, 2021, 15(4): 253-262.
[2] He C, Shen Y, Forbes A. Towards higher-dimensional structured
light [J]. Light: Science & Applications, 2022, 11(1): 205.
[3] Buono W T, Forbes A. Nonlinear optics with structured light [J]. Opto-Electronic Advances, 2022, 5(6): 210174.
[4]Wu H J, Mao L W, Yang Y J, et al. Radial modal transitions of Laguerre-Gauss modes during parametric up-conversion:
Towards the full-field selection rule of spatial modes [J]. Physical Review A, 2020, 101(6): 063805.
[5]Wu H J, Yang H R, Rosales-guzmánC, et al. Vectorial nonlinear optics: Type-II second-harmonic generation driven by spin-orbit- coupled fields [J]. Physical Review A, 2019, 100(5): 053840.
[6] Yang H R, Wu H J, Gao W, et al. Parametric upconversion of Ince-Gaussian modes [J]. Optics Letters, 2020, 45(11): 3034- 3037.
[7] Wu H J, Yu B S, Jiang J Q, et al. Observation of anomalous orbital angular momentum transfer in parametric nonlinearity [J]. Physical Review Letters, 2023, 130(15): 153803.
[8] Zhou Zhiyuan, Shi Baosen. Progresses in infrared detection based on spectrum transducing (invited) [J]. Infrared and Laser Engineering, 2023, 52(5): 20230165. (in Chinese)
[9] Wu H J, Yu B S, Zhu Z H, et al. Conformal frequency conversion for arbitrary vectorial structured light [J]. Optica,2022, 9(2): 187-196.
[10] Wu H J, Zhao B, Rosales-guzmán C, et al. Spatial-polarization- independent parametric up-conversion of vectorially structured light [J]. Physical Review Applied, 2020, 13(6): 064041.
[ 11] Jiang J Q, Wu H J, Yu B S, et al. Nonlinear orbital angular momentum conversion with spatial-amplitude independence [J]. Journal of Optics, 2022, 25(2): 024004.
[12] Yu B S, Li C Y, Yang Y, et al. Directly determining orbital angular momentum of ultrashort laguerre-Gauss pulses via spatially-resolved autocorrelation measurement [J]. Laser & Photonics Reviews, 2022, 16(9): 2200260.
[13] Li C Y, Liu S J, Yu B S, et al. Toward arbitrary Spin-Orbit flat optics via structured geometric phase gratings [J]. Laser & Photonics Reviews, 2023, 17(5): 2200800.
文章来源:《红外与激光工程》第 52 卷第 8 期
作者:吴海俊,于丙石,姜嘉琪,赵 波,Carmelo Rosales-Guzmán,白振旭,朱智涵,史保森
声明:转载此文目的在于传递更多信息,仅供读者学习、交流之目的。文章版权归原作者所有,如有侵权,请联系删除。
这篇关于【探讨】光场空间结构全维度非线性调控理论及应用的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




