本文主要是介绍sigmoid函数温习【函数曲线可视化与导函数曲线可视化】,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
今天晚上遇到一个问题就是sigmoid函数,我只记得sigmoid函数的原始函数曲线是什么样子的,但是导函数是什么样子我还真的是不记得了,恰巧就被问到了这个问题,还顺便问了一下导函数的取值范围是多少,如果当时有纸和笔的话我倒是可是现场算一算的,但是当时是在阳台上没有办法去算,尴尬......
结束了这一次的尴尬之后,回到工位上抓紧温习一下,先绘制一下sigmoid和其导函数的曲线,如下:
#!usr/bin/env python
# encoding:utf-8
from __future__ import division"""
__Author__:沂水寒城
功能: sigmoid函数分析
"""import numpy as np
import matplotlib.pyplot as pltdef sigmoid(x):'''定义sigmoid函数'''return 1.0/(1.0+np.exp(-x))def sigmoidDerivative(x):'''定义sigmoid导函数'''return sigmoid(x)*(1-sigmoid(x))def sigmoidPloter(start=-10,end=10,save_path='sigmoid.png'):'''绘制sigmoid函数曲线'''x=np.arange(start,end,0.1)y=sigmoid(x)y2=sigmoidDerivative(x) plt.plot(x,y,label='sigmoid')plt.plot(x,y2,label='sigmoidDerivative')plt.title('sigmoid sigmoidDerivative')plt.legend()plt.savefig(save_path)if __name__ == '__main__':sigmoidPloter(start=-100,end=100,save_path='sigmoid.png')因为sigmoid是以点(0,0,5)为中心的旋转对称结构,我们这里设置x轴坐标的时候也是设置了对称的形式,便于更加直观地展现出来sigmoid曲线的特性。
start=-10,end=10时图像如下:

start=-100,end=100时图像如下:

一图胜过千言万语,能够很直观地看出来sigmoid的形状了。
接下来从公式角度来进行分析:
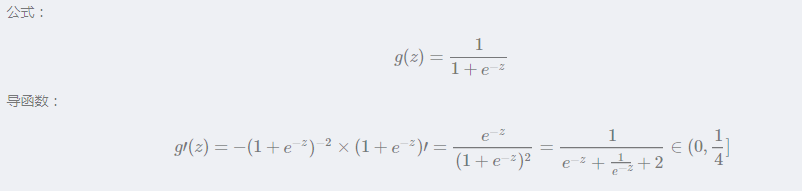
结合图像,我们可以看到:sigmoid函数的取值范围在(0,1)之间
sigmoid导函数取值范围在(0,0.25]之间
学习记录一下,每天学习一点点!
这篇关于sigmoid函数温习【函数曲线可视化与导函数曲线可视化】的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






