TR4 - Transformer中的多头注意力机制

本文主要是介绍TR4 - Transformer中的多头注意力机制，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

---

---

前言

多头注意力机制可以说是Transformer中最主要的模块，没有之一。这次我们来仔细分析一下注意力机制与多头注意力机制。

自注意力机制

在Transformer模型中，输入的文本序列经过输入处理转换为一个向量的序列，然后就会被送到第1层的编码器，第一层的编码器的输出同样是一个向量的序列，再送到下一层编码器。

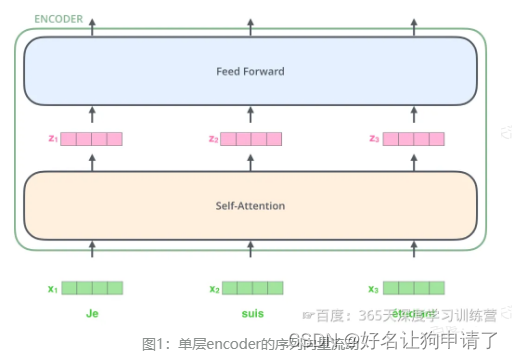
通过上图可以发现，向量在层间流动时，向量的数量和维度都是不变的。单层编码器接收到上一层的输入，然后进入自注意力层计算，然后再输入到前馈神经网络中，最后得到每个位置的新向量。

Self-Attention层的具体机制

例如想要翻译的句子为：“The animal didn’t cross the street because it was too tired”。

句子中的it是一个代词，想要知道它具体代指什么，对模型来说并不容易。通过引用Self-Attention机制，模型就会最终计算出it代指的是animal。同样的，当模型处理句子中其他词时，Self-Attention机制也可以让模型不仅仅关注当前位置的词，还关注句中其它位置相关的词，进而更好地理解当前位置的词。

通过一个简单的例子来解释自注意力机制的计算过程：假设一句话为"Thinking Machines"。

自注意力会计算：Thinking-Thinking、Thinking-Machines、Machines-Thinking、Machines-Machines共2的2次方种组合。

具体的计算过程如下：

• 1 对输入编码器的词向量进行线性变换，得到Query、Key和Value向量。变换的过程是通过词向量分别和3个参数矩阵相乘，参数矩阵可以通过模型训练学习到。

• 2 计算 Attention Score （注意力分数 ）。

假如我们现在计算Thinking的Attention Score，需要根据Thinking对应的词向量，对句子中的其他词向量都计算一个分数，这些分数决定了在编码Thinking这个词时，对句子中其它位置的词向量的权重。

Attention Score 是根据Thinking对应的Query向量和其他位置的每个词的Key向量进行点积得到的。Thinking的第一个Attention Score 就是q1和k1的点积，第二个分数是$q_1$和$k_2$的点积。

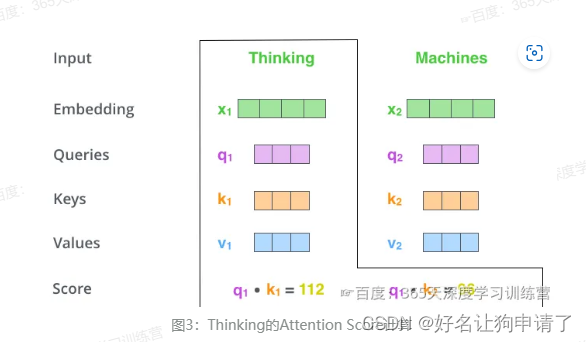
• 3 把得到的每个分数除以$\sqrt{d_k}$。$d_k$是Key向量的维度。这一步的目的是为了在反向传播时，求梯度时更加稳定。

$scor{e}_{11}=\frac{q_1\cdot k_1}{\sqrt{d_k}}$

$scor{e}_{12}=\frac{q_1\cdot k_2}{\sqrt{d_k}}$

• 4 然后把分数经过一个Softmax函数，通过Softmax将分数归一化，使分数都是正数并且加起来等于1。

$scor{e}_{11}=softmax(scor{e}_{11})$

$scor{e}_{12}=softmax(scor{e}_{12})$

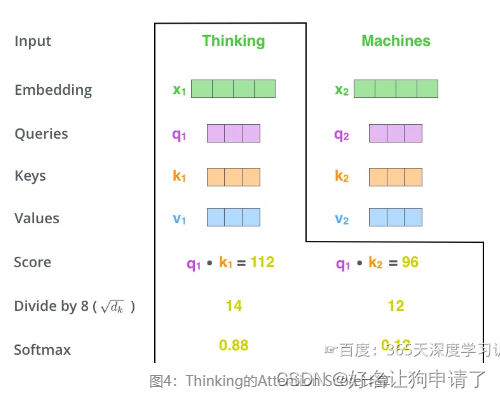
• 5 得到每个词向量的分数后，将分数分别与对应的Value向量相乘。对于分数高的位置，相乘后的值就越大，我们把更多的注意力放到了它们的身上；对于分数低的位置，相乘后的值就越小，这些位置的词可能就相关性不大。
  
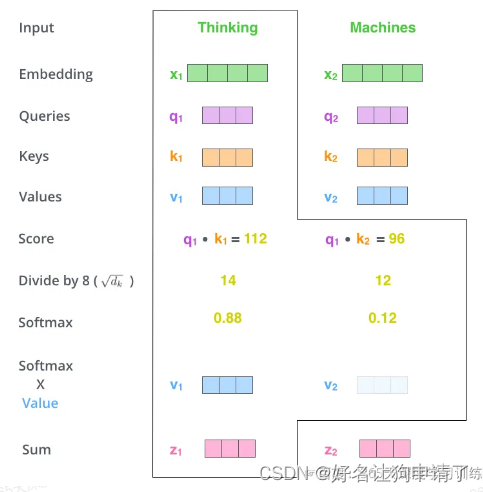
• 6 把第5步得到的Value向量相加，就得到了Self-Attention在当前位置对应的输出

$z_1=v_1\times scor{e}_{11}+v_2\times scor{e}_{12}$

最后整体看一下Self-Attention计算的全过程

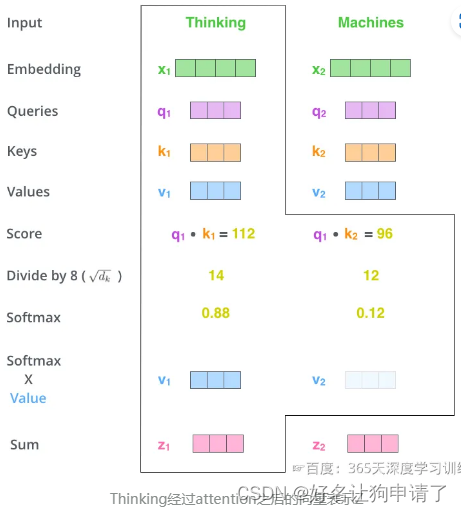
Self-Attention 矩阵计算

具体的实现时，并不会像上面那样阶段分明的分成6个步骤，而是将向量合并到一起，进行矩阵运算。

$X_1$： 第一个单词的输入向量
$X_2$： 第二个单词的输入向量
$X=[X_1;X_2]$ 将两个向量合并为矩阵

具体来说分为了两步：

• 1：计算Query、Key、Value的矩阵。

  $Q=X{W}^Q$：计算Query

  $K=X{W}^K$：计算Key

  $V=X{W}^V$：计算Value

  把所有的词向量放到一个矩阵X中，然后分别和3个权重矩阵$W^Q$、$W^K$、$W^V$相乘，得到 $Q$、$K$、$V$矩阵。矩阵X中的每一行，表示句子中的每一个词的词向量。$Q$、$K$、$V$矩阵中的每一行表示Query向量、Key向量、Value向量，向量的维度是$d_k$。

  

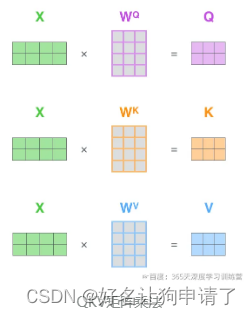
• 2：矩阵计算把上面第2步到第6步压缩为一步，直接得到Self-Attention的输出

  $Z=softmax(\frac{Q{K}^T}{\sqrt{d_k}})\times V$

  

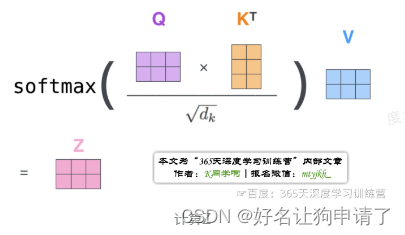
多头注意力机制

Transformer的论文中，通过增加多头注意力机制（一组注意力称为一个Attention Head），进一步完善了Self-Attention。这种机制从如下两个方面增强了Attention层的能力：

• 扩展了模型关注不同位置的能力

  在上面的例子中，第一个位置的输出$z_1$包含了句子中其他每个位置的很小一部分信息。但$z_1$仅仅是单个向量，所以可能仅由第1个位置的信息主导了。而当我们翻译句子：The animal didn't cross the street because it was too tired时，我们不仅希望模型关注到it本身，还希望模型关注到The和animal，甚至关注到tired。

• 多头注意力机制赋予了Attention层多个“子表示空间”

  多头注意力机制会有多组$W^Q$、$W^K$、$W^V$的权重矩阵，因此可以将$X$变换到更多种子空间中进行表示 。
  
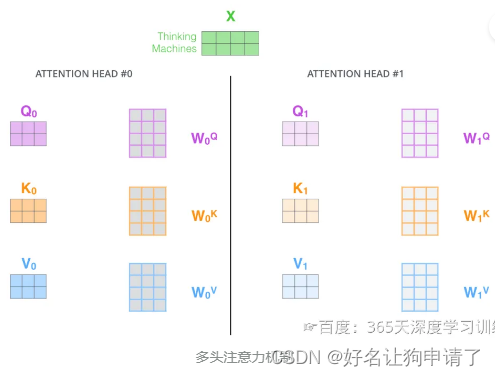
  每组注意力设定单独的$W^Q$、$W^K$、$W^V$参数矩阵。将输入$X$与它们相乘，得到多组$Q$、$K$、$V$矩阵。接下来把每组的$Q$、$K$、$V$计算得到各自的$Z$。
  
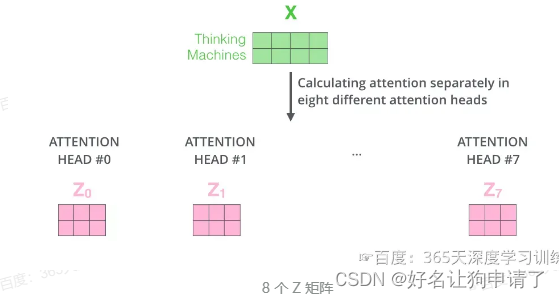
  由于前馈神经网络层接收的是1个矩阵（其中每行的向量表示一个词），而不是8个矩阵，所以要直接把8个子矩阵拼接得到一个大矩阵，然后和另一个权重矩阵$W^O$相乘做一次变换，映射到前馈神经网络层所需要的维度。
  
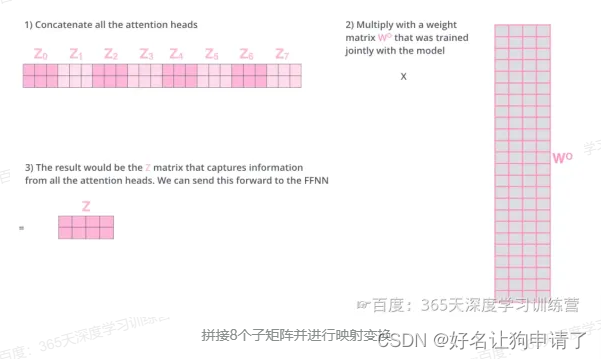
  把多头注意力放到一张图中：
  

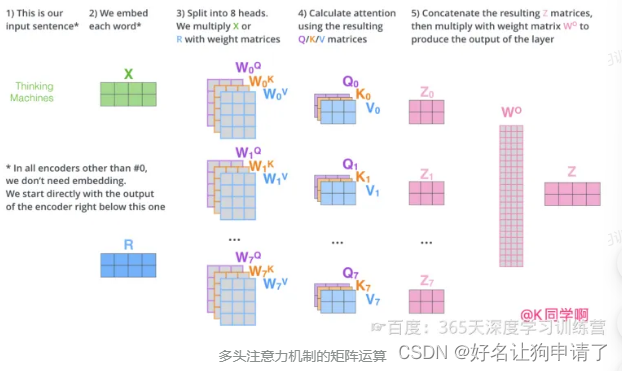
例子解析

再来看一下上面提到的it的例子，不同的Attention Heads对应的it attention了哪些内容。

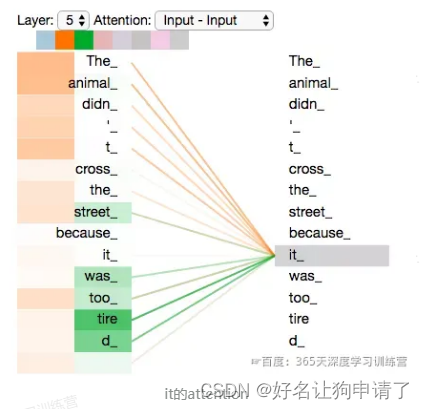
图中绿色和橙色线条分别表示2组不同的Attention Heads。可以看到，当我们编码单词it时，其中一个Attention Head（橙色）最关注的是the animal，另外一个绿色Attention Head关注的是tired。因此在某种意义上，it在模型中的表示，融合了animal和tire的部分表达。

代码实现

class MultiHeadAttention(nn.Module):def __init__(self, hid_dim, n_heads, dropout):super().__init__()self.hid_dim = hid_dimself.n_heads = n_heads# hid_dim必须整除assert hid_dim % n_heads == 0# 定义wqself.w_q = nn.Linear(hid_dim, hid_dim)# 定义wkself.w_k = nn.Linear(hid_dim, hid_dim)# 定义wvself.w_v = nn.Linear(hid_dim, hid_dim)self.fc = nn.Linear(hid_dim, hid_dim)self.do = nn.Dropout(dropout)self.scale = torch.sqrt(torch.FloatTensor([hid_dim//n_heads]))def forward(self, query, key, value, mask=None):# Q与KV在句子长度这一个维度上数值可以不一样bsz = query.shape[0]Q = self.w_q(query)K = self.w_k(key)V = self.w_v(value)# 将QKV拆成多组，方案是将向量直接拆开了# (64, 12, 300) -> (64, 12, 6, 50) -> (64, 6, 12, 50)# (64, 10, 300) -> (64, 10, 6, 50) -> (64, 6, 10, 50)# (64, 10, 300) -> (64, 10, 6, 50) -> (64, 6, 10, 50)Q = Q.view(bsz, -1, self.n_heads, self.hid_dim//self.n_heads).permute(0, 2, 1, 3)K = K.view(bsz, -1, self.n_heads, self.hid_dim//self.n_heads).permute(0, 2, 1, 3)V = V.view(bsz, -1, self.n_heads, self.hid_dim//self.n_heads).permute(0, 2, 1, 3)# 第1步，Q x K / scale# (64, 6, 12, 50) x (64, 6, 50, 10) -> (64, 6, 12, 10)attention = torch.matmul(Q, K.permute(0, 1, 3, 2)) / self.scale# 需要mask掉的地方，attention设置的很小很小if mask is not None:attention = attention.masked_fill(mask == 0, -1e10)# 第2步，做softmax 再dropout得到attentionattention = self.do(torch.softmax(attention, dim=-1))# 第3步，attention结果与k相乘，得到多头注意力的结果# (64, 6, 12, 10) x (64, 6, 10, 50) -> (64, 6, 12, 50)x = torch.matmul(attention, V)# 把结果转回去# (64, 6, 12, 50) -> (64, 12, 6, 50)x = x.permute(0, 2, 1, 3).contiguous()# 把结果合并# (64, 12, 6, 50) -> (64, 12, 300)x = x.view(bsz, -1, self.n_heads * (self.hid_dim // self.n_heads))x = self.fc(x)return x        

测试一下是否能输出

query = torch.rand(64, 12, 300)
key = torch.rand(64, 10, 300)
value = torch.rand(64, 10, 300)
attention = MultiHeadAttention(hid_dim=300, n_heads=6, dropout=0.1)
output = attention(query, key, value)
print(output.shape)

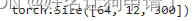
总结与心得体会

通过对多头注意力机制的学习，有一个让我印象深刻的地方就是，它的多头注意力机制不是像其它模块设计思路一样，对同一个输入做了多组运算，而是将输入切分成不同的部分，每部分分别做了多组运算。由于自然语言处理中，一个单词的词向量往往是很长的，所以这种方式比CV的那种堆叠的方式能减少很多计算量，并且在效果方面不会损失太多。

个人感觉：词向量的不同分组之间的关系有点像计算机视觉中，彩色图像的多个通道，多头注意力机制有点像后面的通道注意力的计算。

这篇关于TR4 - Transformer中的多头注意力机制的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---