用三元组存储稀疏矩阵并实现转置

本文主要是介绍用三元组存储稀疏矩阵并实现转置，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

基本概念

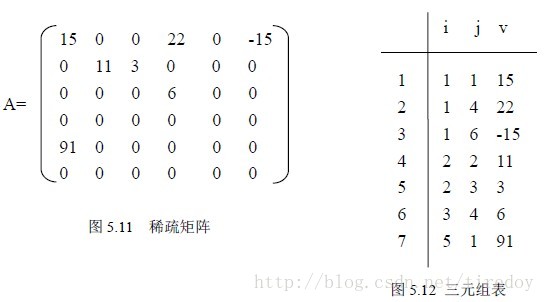
在学习线性代数的时候，经常用到矩阵。在C语言中，表示矩阵的最直观形式就是二维数组。然而在实际应用中，很多高阶矩阵中的非零元素非常少，这个时候如果继续使用二维数组存储，那么就会浪费很多存储空间。

在数据结构中，我们用三元组存储稀疏矩阵。三元组定义为(i,v,j)，这三个值一次表示矩阵的行、列、值。

有了基本的概念之后，就可以定义数据结构了

定义一个结构体，来表示三元组的基本属性

typedef struct
{int row, col;int e;
}Triple;

然后再定义一个存储容器，用来存放三元组的

为了简单起见，我们用数组来实现，并定义最大存储单元MAXSIZE为100

typedef struct
{Triple data[MAXSIZE];Int m,n,len;
}TSMatrix;
//(TSMatrix表示 Triple Sparse Matrix)

实现矩阵的转置
实现用三元组表示的矩阵的转置，可以直接把行列互换，然后再执行按行序为主的排序过程。为了避免重新排序引起的元素移动，可以采用列序递增转置法。

具体做法，就是遍历列的下表值，从列数低的值到列数高的值，依次添加到缓存三元组中。很显然，这是一个双重for循环结构，内层循环实现遍历整个表，寻找合适的列。外层循环，则记录要寻找的列数。

//实现转置 
void TransposeTSMatrix(TSMatrix A, TSMatrix* B)
{int i,j,k;B->m = A.n;B->n = A.m;B->len = A.len;j=0;for( k=0; k<A.len; ++k){for( i=0; i<A.len; ++i){if(A.data[i].col == k){B->data[j].row = A.data[i].col;B->data[j].col = A.data[i].row;B->data[j].e = A.data[i].e;++j;}}}}

有了上面的基础，就可以写一个带有测试驱动的函数

完整代码

#include <stdio.h>
#define MAXSIZE 100
//三元组的定义 
typedef struct
{int row, col;//表示行列 int e;		//表示值 
}Triple;//三元组容器的定义 
typedef struct
{Triple data[MAXSIZE];int m,n,len;
}TSMatrix;//实现转置 
void TransposeTSMatrix(TSMatrix A, TSMatrix* B)
{int i,j,k;B->m = A.n;B->n = A.m;B->len = A.len;j=0;for( k=0; k<A.len; ++k){for( i=0; i<A.len; ++i){if(A.data[i].col == k){B->data[j].row = A.data[i].col;B->data[j].col = A.data[i].row;B->data[j].e = A.data[i].e;++j;}}}}//测试驱动函数 
int main()
{//将输入重定向到根目录下的data.txt freopen("data.txt", "r", stdin);TSMatrix A,B;int i,j,e; int k=0;printf("请输入三元组：");while(scanf("%d%d%d", &i, &j, &e)!=EOF){A.data[k].row = i-1;A.data[k].col = j-1;A.data[k].e = e;A.len = ++k;}printf("\n原始三元组为:\n");for(i=0; i<A.len; ++i ){printf("%3d%3d%3d\n", A.data[i].row+1, A.data[i].col+1, A.data[i].e);}printf("\n转置后:\n");TransposeTSMatrix(A, &B);for(i=0; i<B.len; ++i ){printf("%3d%3d%3d\n", B.data[i].row+1, B.data[i].col+1, B.data[i].e);}return 0;
}

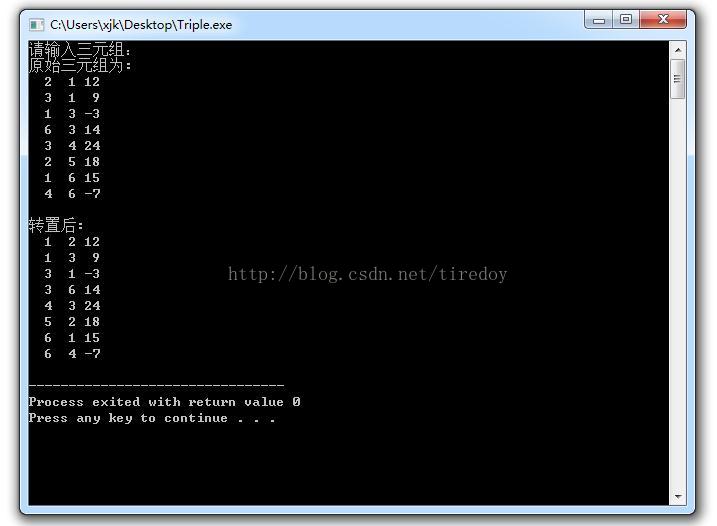
程序截图