本文主要是介绍【TWVRP】基于matlab遗传算法求解带时间窗的含充电站车辆路径规划问题【含Matlab源码 1177期】,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
✅博主简介:热爱科研的Matlab仿真开发者,修心和技术同步精进,Matlab项目合作可私信。
🍎个人主页:海神之光
🏆代码获取方式:
海神之光Matlab王者学习之路—代码获取方式
⛳️座右铭:行百里者,半于九十。
更多Matlab仿真内容点击👇
Matlab图像处理(进阶版)
路径规划(Matlab)
神经网络预测与分类(Matlab)
优化求解(Matlab)
语音处理(Matlab)
信号处理(Matlab)
车间调度(Matlab)
⛄一、VRP简介
1 VRP基本原理
车辆路径规划问题(Vehicle Routing Problem,VRP)是运筹学里重要的研究问题之一。VRP关注有一个供货商与K个销售点的路径规划的情况,可以简述为:对一系列发货点和收货点,组织调用一定的车辆,安排适当的行车路线,使车辆有序地通过它们,在满足指定的约束条件下(例如:货物的需求量与发货量,交发货时间,车辆容量限制,行驶里程限制,行驶时间限制等),力争实现一定的目标(如车辆空驶总里程最短,运输总费用最低,车辆按一定时间到达,使用的车辆数最小等)。
VRP的图例如下所示:
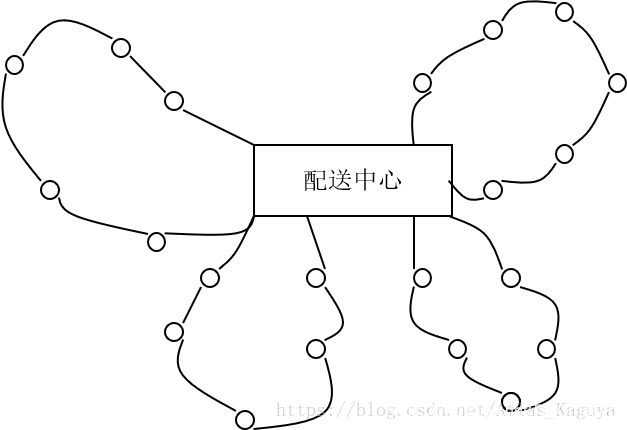
2 问题属性与常见问题
车辆路径问题的特性比较复杂,总的来说包含四个方面的属性:
(1)地址特性包括:车场数目、需求类型、作业要求。
(2)车辆特性包括:车辆数量、载重量约束、可运载品种约束、运行路线约束、工作时间约束。
(3)问题的其他特性。
(4)目标函数可能是总成本极小化,或者极小化最大作业成本,或者最大化准时作业。
3 常见问题有以下几类:
(1)旅行商问题
(2)带容量约束的车辆路线问题(CVRP)



该模型很难拓展到VRP的其他场景,并且不知道具体车辆的执行路径,因此对其模型继续改进。



(3)带时间窗的车辆路线问题
由于VRP问题的持续发展,考虑需求点对于车辆到达的时间有所要求之下,在车辆途程问题之中加入时窗的限制,便成为带时间窗车辆路径问题(VRP with Time Windows, VRPTW)。带时间窗车辆路径问题(VRPTW)是在VRP上加上了客户的被访问的时间窗约束。在VRPTW问题中,除了行驶成本之外, 成本函数还要包括由于早到某个客户而引起的等待时间和客户需要的服务时间。在VRPTW中,车辆除了要满足VRP问题的限制之外,还必须要满足需求点的时窗限制,而需求点的时窗限制可以分为两种,一种是硬时窗(Hard Time Window),硬时窗要求车辆必须要在时窗内到达,早到必须等待,而迟到则拒收;另一种是软时窗(Soft Time Window),不一定要在时窗内到达,但是在时窗之外到达必须要处罚,以处罚替代等待与拒收是软时窗与硬时窗最大的不同。


模型2(参考2017 A generalized formulation for vehicle routing problems):
该模型为2维决策变量

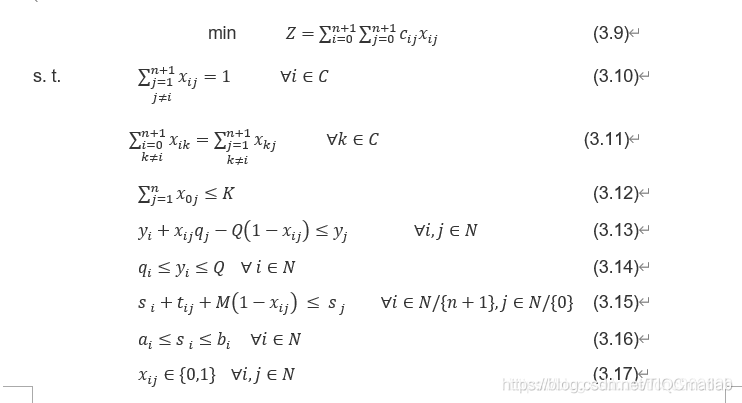

(4)收集和分发问题
(5)多车场车辆路线问题
参考(2005 lim,多车场车辆路径问题的遗传算法_邹彤, 1996 renaud)
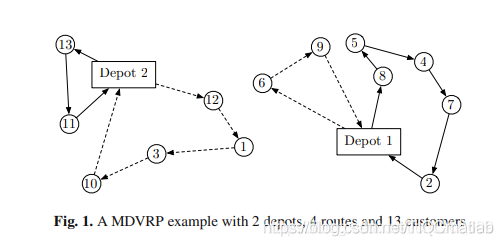
由于车辆是同质的,这里的建模在变量中没有加入车辆的维度。


(6)优先约束车辆路线问题
(7)相容性约束车辆路线问题
(8)随机需求车辆路线问题
4 解决方案
(1)数学解析法
(2)人机交互法
(3)先分组再排路线法
(4)先排路线再分组法
(5)节省或插入法
(6)改善或交换法
(7)数学规划近似法
(8)启发式算法
5 VRP与VRPTW对比
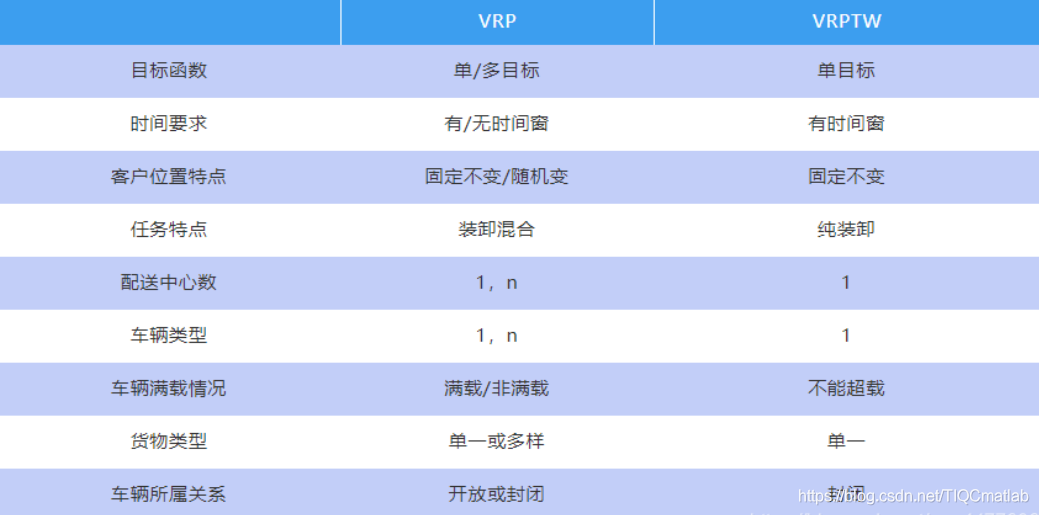
⛄二、遗传算法简介
1 遗传算法的思想来源
遗传算法是建立在自然选择学说基础之上的智能算法。生物种群在自然选择中优胜劣汰,代代繁衍。每一次种群更替,总是淘汰劣质基因、保留优质基因,从而朝着种群的最优发展方向进化。
生物遗传是生物种群不断靠近全局最优解的过程,那么我们能不能用这个思路来解决最优化问题呢?
当然可以:仿照自然遗传过程,①人为设定一个数据组作为“种群基因”,②以目标函数作为评判“发展方向优劣”的标准;③让这群数据通过计算机模拟的“交配”、“基因突变”、“种群复制”等自然选择过程,不断迭代更新、优胜劣汰;④基因趋于稳定时,我们称其为“成熟”,就得出问题的全局最优解。
2 遗传算法的原理分析
①建立种群的基因库------二进制编码
②实现遗传过程的交配、突变、选择遗传等过程
1)依适应度的概率选择规则
生物繁衍过程,种群的生老病死,基因是否突变,基因是否顺利遗传,哪两个基因发生交配等问题都是不确定的概率问题。因此,我们不能用绝对的标准控制某个基因的遗传情况。
因此,我们只能通过抽奖的方式,将某个个体被抽到的概率与其生存能力(适应度)挂钩。生存能力越强,适应度越大,自然也就有更大机会被选中,进行遗传行为了。
生物繁衍过程的适应度是指:生物生存技能、生物体质是否壮硕等指标。类似的,求解函数的最大值问题时,我们自然将自变量的函数值作为适应度了。函数值越大、它适应度越大,越容易被抽中。
同理,当求解最小值优化问题时,应构造适应度函数,使得函数值越小,适应度越大。
2)新种群复制
种群复制: 该步骤主要为选择一定数量的染色体复制到下一代,是实现“优胜劣汰”的关键步骤。每个个体是否能被遗传到下一代,由上述提到的个体适应度决定。
但是,这里存在两种复制方案,我认为有必要在这里说明一下:
① 将适应度从大到小进行排序,选取适应度最优的P_0个个体遗传到下一代
②依照适应度大小,得出被遗传的概率大小,依照概率随机抽选个体遗传。该方法中,最优个体有可能在复制中被丢失;最差个体也有可能被复制到下一代。
部分小伙伴可能理所当然认为①是最合理的。但并不是,两种方法有其各自的应用范围。下面分别谈谈:
1、办法①在求解一些简单的优化问题,通常局部最优即为全局最优解的问题是适用的。但是,每一步都只保留优秀个体而损失不良个体,可能会被“暂时的优秀”,即局部最优所蒙蔽。这种做法在面对复杂函数时,会失去一定的全局搜索能力。
3)新种群交配(交叉)
每次交叉的两个染色体为步骤2)中选出的染色体,将其序号作为参数传入crossover子函数中,是否交配遵循以下规则:
①依交叉概率pcrossover,使用下函数随机决定两个染色体是否发生交叉(后面判断是否变异也用它)。
②若发生交叉,再使用rand函数抽取一个交叉节点,将两个染色体节点前、后的部分交叉。
4)基因突变
基因变异即将基因序列上的某一位进行0-1翻转。变异的基因为由rand函数随机产生。
是否发生变异由变异概率pmutation决定。
5)主函数 遗传迭代
将函数块组合到主函数中,进行遗传迭代。
⛄三、部分源代码
%% 包括充电站1
clc;
clear all
close all
filename=‘.\evrptw_instances\c101_21.txt’;
[NO,type,XCOORD, YCOORD,DEMAND,READY_TIME,DUE_DATE,SERVICE_TIME]=textread(filename,‘%s%s%s%s%s%s%s%s’,‘headerlines’,1);
%% 进行经验求解路径
K=randperm(100);%对客户点随机排序
M=30;%任务量
capacity = 200;%车子载重
timewindows_yuanshi=[str2num(char(READY_TIME))‘;str2num(char(DUE_DATE))’];%时间窗
coordinate_yuanshi=[str2num(char(XCOORD)),str2num(char(YCOORD))];%坐标信息
coordinate_chongdianzhan=[coordinate_yuanshi(2:22,1)‘;coordinate_yuanshi(2:22,2)’;]‘;%充电站坐标
demand_yuanshi=str2num(char(DEMAND))’;%所有需求
service_yuanshi=str2num(char(SERVICE_TIME))‘;%所有服务时间
D=distanse(coordinate_yuanshi);%距离1
coordinate=[coordinate_yuanshi(1,1),coordinate_yuanshi(K(1:M)+22,1)’;coordinate_yuanshi(1,2),coordinate_yuanshi(K(1:M)+22,2)‘;]’;%中心和客户坐标位置
timewindows=[timewindows_yuanshi(1,1),timewindows_yuanshi(1,K(1:M)+22) ;timewindows_yuanshi(1,2),timewindows_yuanshi(2,K(1:M)+22)];%随机选取的客户点时间窗
demand=[demand_yuanshi(1),demand_yuanshi(K(1:M)+22)];%随机选取的客户点需求
service=[service_yuanshi(1),service_yuanshi(K(1:M))+22];%随机选取的客户点服务时间
% coordinate_yuanshi1=[coordinate_yuanshi(1,1),coordinate_yuanshi(23:end,1)‘;coordinate_yuanshi(1,2),coordinate_yuanshi(23:end,2)’;]';%中心和客户坐标位置
% D1=distanse(coordinate_yuanshi1);%距离
D2=distanse(coordinate);%距离
renwudian1=[1,K(1:M)+1];%包括起点的任务点
Q=77.751111;%电量
r=1;%消耗率
g=0.39;%充电
v=1;%速度
% %% 遗传参数初始化
C=500;%C为停止代数,遗传到第 C代时程序停止,C的具体取值视问题的规模和耗费的时间而定
Pc=0.9;%交叉概率
Pm=0.4;%变异概率
popsize=80;%种群数量
%经验公式m=[Σgi /aq]+1,粗求车辆数
function [ farm ] = crossover( farm,n,k,popsize,Pc )
%CROSSOVER Summary of this function goes here
% Detailed explanation goes here
% ⑴随机产生交叉位,如果在交叉位的外侧两端的父代基因都是0的话,则对父代1
% 进行简单交叉;如果交叉位的外侧两端的父代基因不为0的话,则将左交叉位向左
% 移,直至移动到左交叉位的左端基因为0时停止。以左交叉位为起点,继续向右移
% 动右交叉位,直至右交叉位的右端基因为0为止。这样就保证了父代染色体都用1条
% 子路径来进行交叉。
% ⑵经过第1步操作,子代中仍会产生访问同一客户2次的情况,需要对
% 子代进行整理。在子代中选择那些具有重复情况的自然数,如果该自然数并非
% 在交叉位内的话,则删除之。子代如存在未访问到某一客户的情况,则在染色
% 体的交叉位外补上该客户对应的自然数。
% ⑶经过第2步的操作,如果产生了某一子路径为空的情况,即染色体中含
% 有2个连续的0,须继续进行第3步操作。将其中的1个0与染色体其它位上
% 的客户自然码进行交换。对该客户自然码的要求是该码的前一位与后一位均不
% 为0。本步操作可放在对子代的变异后进行。
function temp = minsert(chrom,num,n)%insert函数,向量中指定位置插入数
%n是要插入的位置(之后)
[x,xx] = size(chrom);
temp = zeros(1,xx+1); %初始化
temp(1,1:n) = chrom(1,1:n);
temp(1,n+1) = num;
temp(1,(n+2):(xx+1)) = chrom(1,(n+1):xx);
end
function temp = mdelete(chrom,n)%delete函数,向量中指定位置删除数
%n是要删除数的坐标
[x,xx] = size(chrom);
temp = zeros(1,xx-1); %初始化
temp(1,1:n-1) = chrom(1,1:n-1);
temp(1,n:xx-1) = chrom(1,(n+1):xx);
end
total = n+k+1;
for i = 1:(popsize/2) %按对进行交叉
if Pc > rand
chromosome1 = zeros(1,total);
chromosome2 = zeros(1,total);
chromosome1 = farm(i,:); %染色体1
chromosome2 = farm(popsize - i + 1,:); %染色体2
%第一步*************************************************************
ran1L = round(rand*(total-3)+2); %随机数1 注意1和最后不要随机到
while chromosome1(1,ran1L) == 0 %不能随机到0
ran1L = round(rand*(total-3)+2);
end
ran1R = ran1L;
ran2L = round(rand*(total-3)+2); %随机数2
while chromosome2(1,ran2L) == 0 %不能随机到0
ran2L = round(rand*(total-3)+2);
end
ran2R = ran2L;
while chromosome1(1,ran1L-1) ~= 0 %左移直至第一个0出现
ran1L = ran1L - 1;
end
while chromosome1(1,ran1R+1) ~= 0 %右移直至第一个0出现
ran1R = ran1R + 1;
end
while chromosome2(1,ran2L-1) ~= 0 %左移直至第一个0出现
ran2L = ran2L - 1;
end
while chromosome2(1,ran2R+1) ~= 0 %右移直至第一个0出现
ran2R = ran2R + 1;
end
%交换片段**********************************************************
temp1 = zeros(1,total); %临时储存
temp2 = zeros(1,total); %临时储存
length1 = ran1R-ran1L+1; %片段长
length2 = ran2R-ran2L+1; %片段长
for ii = 1:length1 %转移到临时储存
temp1(1,ii) = chromosome1(1,ran1L+ii-1);
end
for ii = 1:length2 %转移到临时储存
temp2(1,ii) = chromosome2(1,ran2L+ii-1);
end
chrom1 = zeros(1,total+length2-length1); %中间染色体1
chrom2 = zeros(1,total+length1-length2); %中间染色体2
%重新拼接染色体***************************************************
chrom1(1,1:ran1L-1) = chromosome1(1,1:ran1L-1);
chrom1(1,ran1L:ran1L+length2-1) = temp2(1,1:length2);
chrom1(1,ran1L+length2:total+length2-length1) = chromosome1(1,ran1R+1:total);
chrom2(1,1:ran2L-1) = chromosome2(1,1:ran2L-1);
chrom2(1,ran2L:ran2L+length1-1) = temp1(1,1:length1);
chrom2(1,ran2L+length1:total+length1-length2) = chromosome2(1,ran2R+1:total);
%第二步*************************************************************
nala1 = zeros(1,total);%搜索temp2中有而temp1中没有的数,那个数1中必定重复
nala11 = zeros(1,total);%存放nala中数的位置
nala2 = zeros(1,total);%搜索temp1中有而temp2中没有的数,那个数2中必定重复
nala22 = zeros(1,total);%存放nala中数的位置
%搜索相互没有的数
kk = 1; %nala的下标 好累啊,wwwww…
for ii = 1:length2
flag = 0;
for j = 1:length1
if temp2(1,ii) == temp1(1,j);
flag = 1;
end
end
if flag == 0
nala1(1,kk) = temp2(1,ii);
kk = kk + 1;
end
end
kk = 1; %nala的下标
for ii = 1:length1
flag = 0;
for j = 1:length2
if temp1(1,ii) == temp2(1,j);
flag = 1;
end
end
if flag == 0
nala2(1,kk) = temp1(1,ii);
kk = kk + 1;
end
end
%将多余的数设为0***************************************************
ii = 1;
while nala1(1,ii) ~= 0
[x,xx] = find(chrom1nala1(1,ii)); %找出重复的位置
j = 1;
while xx(1,j) >= ran1L && xx(1,j) <= ran1L+length2-1
j = j + 1;
end
nala11(1,ii) = xx(1,j); %将重复数的位置保存下来
chrom1(1,xx(1,j)) = 0; %%重复的数变为零
ii = ii + 1;
end
ii = 1;
while nala2(1,ii) ~= 0
[x,xx] = find(chrom2nala2(1,ii)); %找出重复的位置
j = 1;
while xx(1,j) >= ran2L && xx(1,j) <= ran2L+length1-1
j = j + 1;
end
nala22(1,ii) = xx(1,j); %将重复数的位置保存下来
chrom2(1,xx(1,j)) = 0; %%重复的数变为零
ii = ii + 1;
end
%补上没有的数******************************************************
[xx,x] = size(nonzeros(nala1));%得到nala的大小
[yy,y] = size(nonzeros(nala2));%得到nala的大小
if yy-xx < 0 %交换后变成yy>xx的情况
%交换
[chrom1,chrom2] = exchange(chrom1,chrom2);
[nala1,nala2] = exchange(nala1,nala2);
[nala11,nala22] = exchange(nala11,nala22);
end
% yy-xx > 0 --> 说明变化后1比2短–>1需要补0并且插入,2需要补0并且删0
% yy-xx < 0 --> 说明变化后2比1短–>2需要补0并且插入,1需要补0并且删0
%补0
ii = 1;
while nala11(1,ii) ~= 0
chrom1(1,nala11(1,ii)) = nala2(1,ii);%1中补0
chrom2(1,nala22(1,ii)) = nala1(1,ii);%2中补0
ii = ii + 1;
end
%||||||||stage3|||||||||
%当前ii在下一位的位置
%1插入&2删除*****************************************************
model1 = chrom1; %用来适应变量维度
model2 = chrom2;
j = 1; %!!!j初始化应该放在while循环外面,小错误不断啊
flag_nala22 = 1;
% %两个chrom的维度是一个问题
% chrom11 = zeros(1,total);
% chrom22 = zeros(1,total);
while nala2(1,ii) ~= 0
%插入,先扩充model->存储变维后的数据;然后chrom扩充,得到model保存的数据
model1 = [model1,0]; %注意顺序
model1 = minsert(chrom1,nala2(1,ii),1);
chrom1 = [chrom1,0];
chrom1 = model1;
%删除0,首先降序排列,用来从后向前删除;之后model变维
while flag_nala22 %又是一个错误,靠,nala22temp每次循环都会被初始化,1次就够了,细心细心,淡定淡定…
nala22temp = zeros(1,total-ii+1);
nala22temp = nala22(1,ii:total);
flag_nala22 = 0;
end
nala22temp = sort(nala22temp);
nala22temp = fliplr(nala22temp);
[q,qq] = size(chrom2);
model2 = zeros(1,qq-1); %注意顺序
model2 = mdelete(chrom2,nala22temp(1,j));
j = j + 1;
chrom2 = zeros(1,qq-1);
chrom2 = model2;
%千万不要忘记迭代+1
ii = ii + 1;
end
farm(i,:) = chrom1;
farm(popsize - i + 1,:) = chrom2;
%在整个算法中,我通过重复的数设0避免了0接着0的情况,很有成就感。
end %交叉概率检测
end %main loop
end %function
⛄四、运行结果
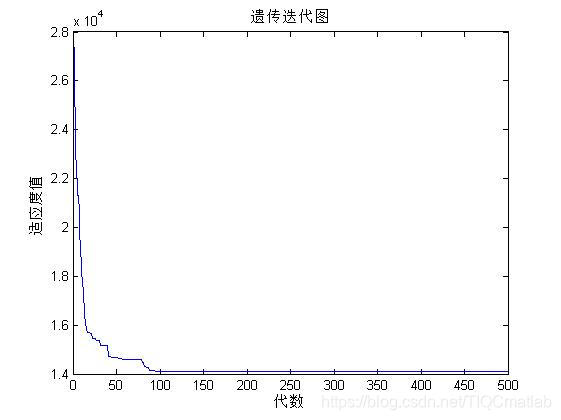
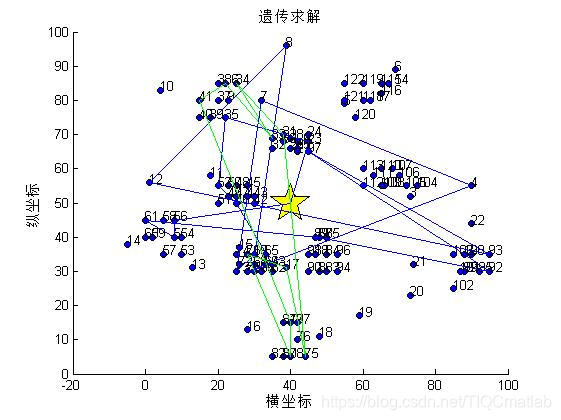
⛄五、matlab版本及参考文献
1 matlab版本
2014a
2 参考文献
[1] 包子阳,余继周,杨杉.智能优化算法及其MATLAB实例(第2版)[M].电子工业出版社,2016.
[2]张岩,吴水根.MATLAB优化算法源代码[M].清华大学出版社,2017.
3 备注
简介此部分摘自互联网,仅供参考,若侵权,联系删除
🍅 仿真咨询
1 各类智能优化算法改进及应用
生产调度、经济调度、装配线调度、充电优化、车间调度、发车优化、水库调度、三维装箱、物流选址、货位优化、公交排班优化、充电桩布局优化、车间布局优化、集装箱船配载优化、水泵组合优化、解医疗资源分配优化、设施布局优化、可视域基站和无人机选址优化
2 机器学习和深度学习方面
卷积神经网络(CNN)、LSTM、支持向量机(SVM)、最小二乘支持向量机(LSSVM)、极限学习机(ELM)、核极限学习机(KELM)、BP、RBF、宽度学习、DBN、RF、RBF、DELM、XGBOOST、TCN实现风电预测、光伏预测、电池寿命预测、辐射源识别、交通流预测、负荷预测、股价预测、PM2.5浓度预测、电池健康状态预测、水体光学参数反演、NLOS信号识别、地铁停车精准预测、变压器故障诊断
3 图像处理方面
图像识别、图像分割、图像检测、图像隐藏、图像配准、图像拼接、图像融合、图像增强、图像压缩感知
4 路径规划方面
旅行商问题(TSP)、车辆路径问题(VRP、MVRP、CVRP、VRPTW等)、无人机三维路径规划、无人机协同、无人机编队、机器人路径规划、栅格地图路径规划、多式联运运输问题、车辆协同无人机路径规划、天线线性阵列分布优化、车间布局优化
5 无人机应用方面
无人机路径规划、无人机控制、无人机编队、无人机协同、无人机任务分配
6 无线传感器定位及布局方面
传感器部署优化、通信协议优化、路由优化、目标定位优化、Dv-Hop定位优化、Leach协议优化、WSN覆盖优化、组播优化、RSSI定位优化
7 信号处理方面
信号识别、信号加密、信号去噪、信号增强、雷达信号处理、信号水印嵌入提取、肌电信号、脑电信号、信号配时优化
8 电力系统方面
微电网优化、无功优化、配电网重构、储能配置
9 元胞自动机方面
交通流 人群疏散 病毒扩散 晶体生长
10 雷达方面
卡尔曼滤波跟踪、航迹关联、航迹融合
这篇关于【TWVRP】基于matlab遗传算法求解带时间窗的含充电站车辆路径规划问题【含Matlab源码 1177期】的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




