本文主要是介绍浅述.Net中的Hash算法(顺带对称、非对称算法),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
【写在前面】
对称加密算法(只有一个私钥,比如DES【不推荐】、AES);
非对称加密算法(公钥与私钥,比如RSA);
Hash算法也称为散列函数算法,任意长度的数据都转换为固定长度的字符串(称为“哈希值”或简称“哈希”)(没有密钥,但可以通过“加盐”增加彩虹表攻击的难度以提高哈希值安全性, 比如MD5、SHA-1【不推荐】、SHA-256、SHA-384、SHA-512),有别于前面两种加密算法,哈希算法具有不可逆性,虽然相同的输入一定得到相同的输出,不同的输入大概率得到不同的输出,但不是绝对,不同的输入也有可能碰撞出相同的哈希值输出(因此哈希算法通常应用于只加密不解密的场景:可用于验证原始数据是否被篡改、存储加密后的密码等)。
在Hash算法的基础上,在来说下HMAC(Hash-based Message Authentication Code,哈希运算消息认证码):HMAC是密钥相关的哈希运算消息认证码,HMAC运算利用哈希算法,以一个密钥(好比Hash加盐处理,但相对加盐有不同的内部处理机制,详可参见 HMAC算法详解 或 HMAC与HS256算法)和一个消息为输入,生成一个消息摘要作为输出,其核心和基础还是Hash算法。

FormsAuthentication.HashPasswordForStoringInConfigFile 实现Hash加密(已弃用)
好,以上是相关背景知识。
今天在一个旧系统中看到这样的密码验证方法,也就是说后台密码存储是以将“用户名+密码”以Hash加密存放的,这里想说的是.Net 4.5中提供的Hash加密方法 FormsAuthentication.HashPasswordForStoringInConfigFile, 通过说明可知该方法已被官方弃用,不再推荐使用,可以在VS2022中反编译进入内部了解其实现细节

以下FormsAuthentication.HashPasswordForStoringInConfigFile的内部实现,从实现的调用中可以看到System.Web.Security.Cryptography.CryptoAlgorithms内部静态类中不仅有创建SHA512方法,还有相应创建HMACSHA512的方法,可做下了解:

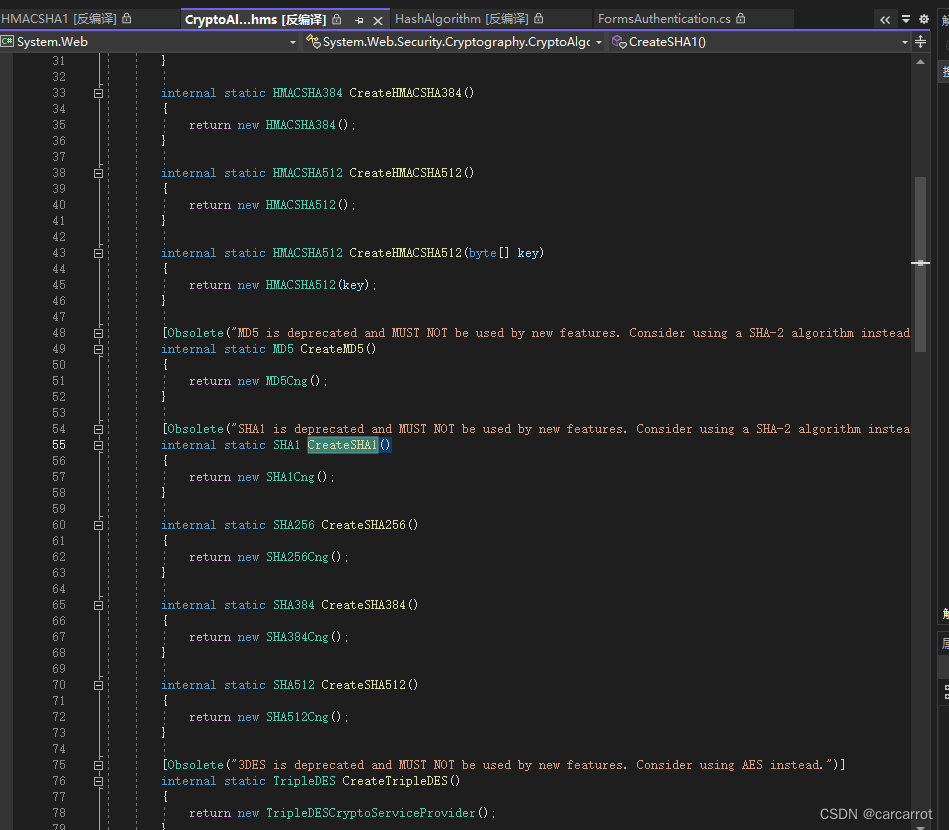
替代方案:XxxCryptoServiceProvider类实现加密算法
既然FormsAuthentication.HashPasswordForStoringInConfigFile已经过时弃用,官方有可用的替代方法吗?当然有,同样在System.Security.Cryptography 命名空间,可以找到SHA1CryptoServiceProvider、MD5CryptoServiceProvider、SHA256CryptoServiceProvider、SHA384CryptoServiceProvider、SHA512CryptoServiceProvider类, (同时也提供了对称算法的DESCryptoServiceProvider 、 AesCryptoServiceProvider 及 非对称算法的RSACryptoServiceProvider)
以下以MD5为例,实现如下:
/// <summary>
/// 32位MD5加密
/// </summary>
/// <param name="input"></param>
/// <returns></returns>
private static string Md5Hash(string input)
{MD5CryptoServiceProvider md5Hasher = new MD5CryptoServiceProvider();byte[] data = md5Hasher.ComputeHash(Encoding.Default.GetBytes(input));StringBuilder sBuilder = new StringBuilder();for (int i = 0; i < data.Length; i++){sBuilder.Append(data[i].ToString("x2"));}return sBuilder.ToString();
}
(附)包括过时及不过时的加解密方法,可以参考:C#实现加密与解密详解_C#教程_脚本之家
这篇关于浅述.Net中的Hash算法(顺带对称、非对称算法)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!








