本文主要是介绍探索性数据分析(EDA),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
- 本篇博客主要介绍的是探索性数据分析以及其Python实现
- 本篇博客内容基于阿里云天池竞赛:心跳信号分类预测写就,着重说明了其探索性数据分析的部分
- 学习交流请联系 obito0401@163.com
文章目录
- 含义
- 内容
- 载入数据处理以及可视化库
- 载入数据
- 数据总览
- 判断数据缺失和异常
- 了解数据分布情况
含义
探索性数据分析(Exploratory Data Analysis,EDA),是指对已有的数据(特别是调查或者观测得来的原始数据)在尽量少的先验假定条件下进行探索,通过作图、制表、方程拟合、计算特征量等手段探索数据的结构和规律的一种数据分析方法。
EDA的价值主要在于了解熟悉数据集,对数据集进行验证来确定所获得的数据集可以用于接下来的机器学习或者深度学习等
内容
载入数据处理以及可视化库
- 数据处理:numpy、pandas、scipy
- 可视化:matplotlib、seabon
import numpy as np
import pandas as pd
import scipy
import matplotlib.pyplot as plt
import seaborn as sns
import missingno as msno # 可视化缺失值
import warnings
warnings.filterwarnings("ignore") # 过滤警告信息
载入数据
- 加载训练集和测试集
data_train = pd.read_csv("train.csv")
data_test = pd.read_csv("testA.csv")
- 简略观察数据(head()、tail()、shape)
# 观察数据集首尾信息
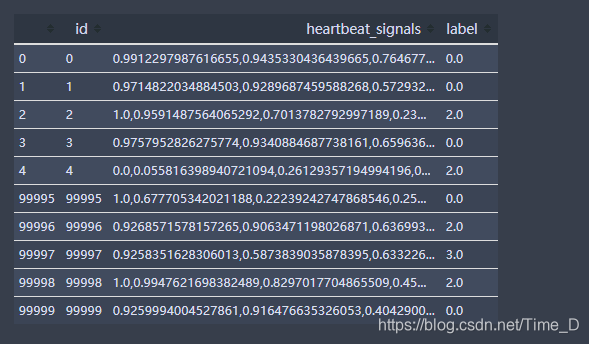
data_train.head().append(data_train.tail())
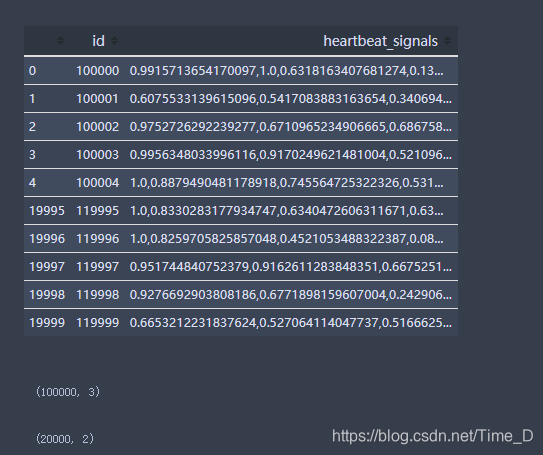
data_test.head().append(data_test.tail())
# 观察数据集大小
data_train.shape
data_test.shape
数据总览
- 通过
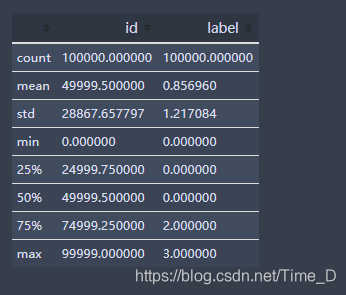
describe()熟悉数据的相关统计量
# 对数据集进行描述统计
data_train.describe()
- 通过
info()熟悉数据类型
# 获取数据集的数据类型
data_train.info()
data_test.info()

判断数据缺失和异常
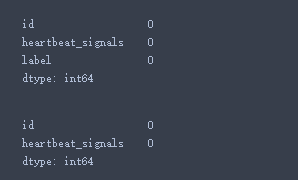
- 查看每列是否存在NA值
# 查看数据集每列的缺失情况
data_train.isnull().sum()
data_test.isnull().sum()
- 异常值检测
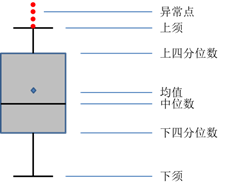
异常值的检测方式一般有以下三种- 根据业务经验划定不同指标的正常范围,超过该范围的值算作异常值
- 通过绘制箱线图,把大于(小于)箱线图上边缘(下边缘)的点称为异常值
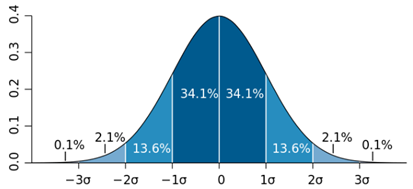
- 如果数据服从正态分布,则可以利用3 σ \sigma σ原则:如果一个数值与平均值之间的偏差超过3倍标准差,那么我们就认为这个值是异常值
了解数据分布情况
- 总体分布概况
import scipy.stats as st
y = data_train["label"]
plt.figure(1); plt.title('Johnson SU') # 无界约翰逊分布
sns.distplot(y, rug=False,kde=True, fit=st.johnsonsu) # rug为地毯图,kde为高斯核函数密度估计
plt.figure(2);plt.title('Normal') # 正态分布
sns.distplot(y,rug=True,kde=False,fit=st.norm)
plt.figure(3);plt.title('Log Normal') # 对数正态分布
sns.distplot(y,rug=True,kde=True,fit=st.lognorm);
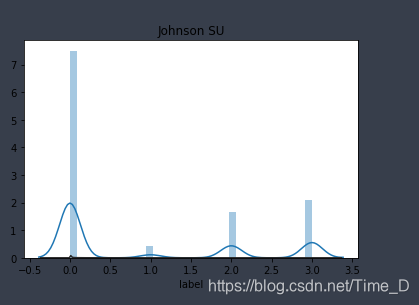
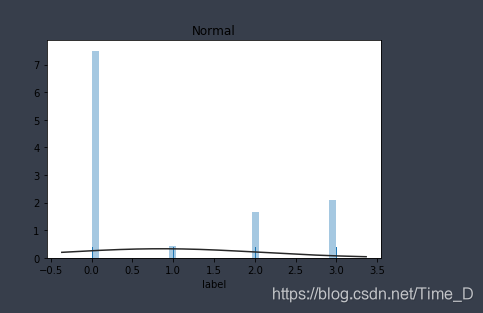
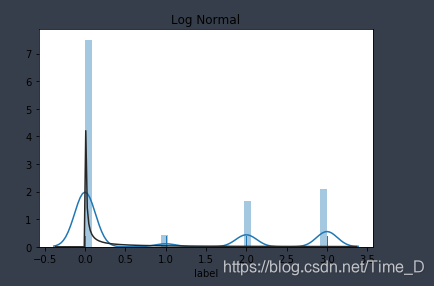
可以看出,总体数据满足对数正态分布
- 偏度和峰度
-
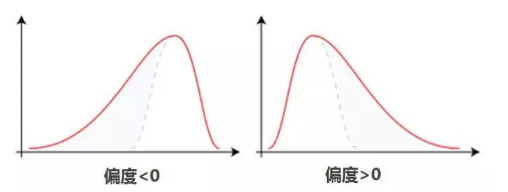
偏度(skewness)用于判断数据分布的形状是否对称以及偏斜的程度
- 如果一组数据分布是对称的,则偏度(偏态系数)等于0
- 如果偏度在大于1或小于-1,则认为是高度偏态分布
- 如果偏度在 0.5 ∼ 1 0.5\sim1 0.5∼1或 − 1 ∼ − 0.5 -1\sim-0.5 −1∼−0.5之间,则认为是中等偏态分布
- 偏度越接近0,则偏斜程度越小
-
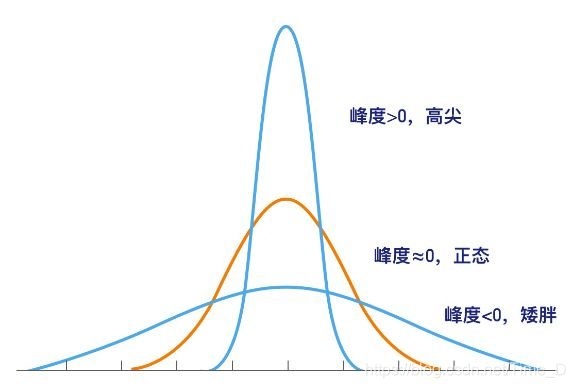
峰度(kurtosis)用于判断数据分布的扁平程度
- 峰态通常是与标准正态分布相比较而言的
- 如果一组数据服从标准正态分布,则峰度(峰态系数)的值等于0
- 如果峰度的值大于0,则为尖峰分布,数据的分布越集中
- 如果峰度的值小于0,则为扁平分布,数据的分布越分散
-
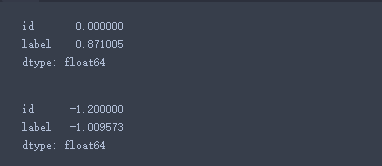
data_train.skew() # 查看偏度
data_train.kurt() # 查看峰度
sns.distplot(data_train.kurt(),axlabel="Kurtness")
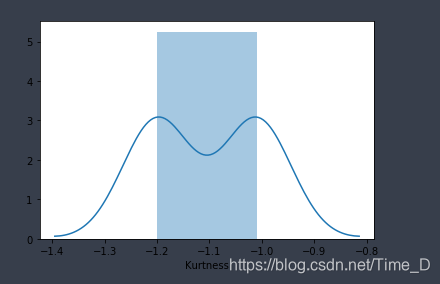
可以看出训练集的数据是右偏扁平分布
- 具体频数
data_train["label"].value_counts()
plt.hist(data_train['label'],orientation="vertical")
plt.show()


这篇关于探索性数据分析(EDA)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!