本文主要是介绍算法练习第12天|● 239. 滑动窗口最大值● 347.前 K 个高频元素,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
239.滑动窗口的最大值
力扣原题
题目描述:
给你一个整数数组 nums,有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。
返回 滑动窗口中的最大值 。
示例 1:
输入:nums = [1,3,-1,-3,5,3,6,7], k = 3 输出:[3,3,5,5,6,7] 解释: 滑动窗口的位置 最大值 --------------- ----- [1 3 -1] -3 5 3 6 7 31 [3 -1 -3] 5 3 6 7 31 3 [-1 -3 5] 3 6 7 51 3 -1 [-3 5 3] 6 7 51 3 -1 -3 [5 3 6] 7 61 3 -1 -3 5 [3 6 7] 7
示例 2:
输入:nums = [1], k = 1 输出:[1]
思路分析:
尝试使用单调队列来记录当前窗口中的最大值。如下图所示,单调队列的入队规则是如果入队的元素前面有比自己小的数,这些数全部被剔除。注意这里说的是剔除,而不是简单的出队。因为如果是单向队列的出队的话,那么单向队列在执行步骤四时可能需要先把数字3出队后才能继续通过出队的方式将-1剔除。这就导致最大值3从队列中消失了。

所以为了更加方面的对多余元素进行剔除,单调队列在用STL容器中的双端deque进行实现,因为deque支持在队列两端进行入队、出队操作。如下图所示。这样在步骤二中的1、步骤四中的-1直接通过pop_back()进行剔除。很方便,而且还能保留最大值。

综上所述,单调队列的目的就是为了维护窗口内最大的两个数。其结构大致长这样:
class MyQueue {
public:void push(int val) {}void pop(int val) {}int front() {return que.front();}
};其中 push(int val) 表示val入队,它的规则是:如果val前面的元素比val小,那么就将这些数通过pop_back弹出,直到遇到比val大的数停止或队列为空停止。如上述的步骤二和步骤四。
pop(int val) 表示val出队,这种情况发生在滑动窗口向右移动的时候。如下图所示:

窗口滑动之后,3不在是窗口内的数,所以需要使用pop_front将单调队列中的3弹出。这里的pop_front也体现出了deque的灵活性。
如果不满足 滑动窗口移动前最左端的值 = 单调队列最左(前)端的值 这个条件,则表明刚才窗口内的最大值还在移动口的窗口内,具体情况如下图所示:
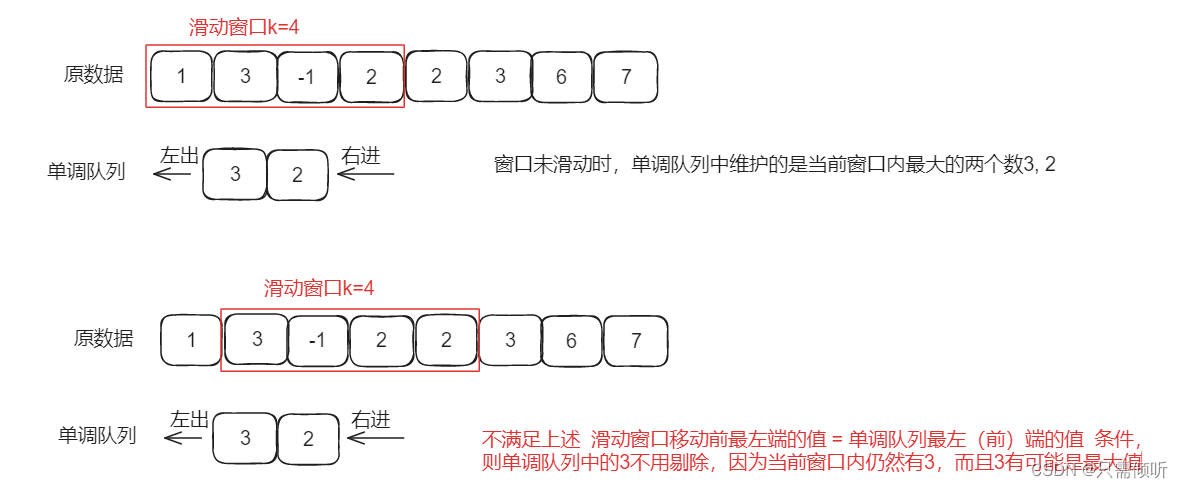
综上所述,该单调队列的代码实现如下:
class myQueue{ //自定义单调队列。从大到小排列,左边出队,右边入队public:deque<int> que; //双端队列void push(int val){ //从队列右端输入数据。若输入的数据val比队列末尾的若干个数大,//则将这些数弹出.直到队列为空或val遇到比自身大的数while(!que.empty() && que.back() < val){que.pop_back(); //循环弹出比val小的数}//val入队que.push_back(val);}void pop(int val) {//比较滑动窗口左端要弹出数值val是否是位于单调//队列左端的最大值,如果是,则弹出;如果不是,表明最大值这个数位于新的窗口内。if(!que.empty() && val == que.front()){que.pop_front();}}int front() //单调队列最左端的值就是当前窗口的最大值{return que.front();}};有了这样的单调队列,下面给出该题的解题代码:
class Solution {
private:class myQueue{ //自定义单调队列。从大到小排列,左边出队,右边入队public:deque<int> que;void push(int val){ //从队列右端输入数据。若输入的数据val比队列末尾的数大,则将该数弹出.直到队列为空或val遇到比自身大的数while(!que.empty() && que.back() < val){que.pop_back(); //循环弹出比val小的数}//val入队que.push_back(val);}void pop(int val) //比较滑动窗口左端要弹出数值val是否是位于单调队列左端的最大值{if(!que.empty() && val == que.front()){que.pop_front();}}int front() //当前窗口的最大值{return que.front();}};public:vector<int> maxSlidingWindow(vector<int>& nums, int k) {myQueue que;vector<int> result;for(int i=0;i<k;i++) //先将前k个数字入队{que.push(nums[i]);}//入队完成后,就只剩下最大的两个数result.push_back(que.front()); //记录当前窗口最大值for(int i = k; i<nums.size();i++)//然后从下标k开始进行窗口移动{//i-k和i的使用非常巧妙地模拟了窗口向右滑动的过程que.pop(nums[i-k]); //窗口滑动先要执行是否pop出来最大值que.push(nums[i]); //新元素入队,重新调整result.push_back(que.front()); // 记录新的最大值}return result;}
};这篇关于算法练习第12天|● 239. 滑动窗口最大值● 347.前 K 个高频元素的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







