《学一辈子光线追踪》二点五五在球面方向的MC积分

本文主要是介绍《学一辈子光线追踪》二点五五在球面方向的MC积分，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

蒙特卡洛光线追踪技术系列见蒙特卡洛光线追踪技术

竟然有两个第二章，我也是很无奈啊。

在我们的光线跟踪器中，我们选择随机方向，方向可以表示为单位球体上的点。采用与之前相同的方法。但现在我们需要在二维上定义一个pdf。假设我们在所有方向上都有这个积分：

INTEGRAL( cos^2(theta) )

即我们需要计算 ∫ cos^2θdθ

通过MC积分，我们应该能够得到 cos^2(theta)/p(direction) 的样本。但在这种情况下，direction是什么？我们可以根据极坐标来计算，所以p是(theta,phi)。但是，请记住，pdf必须积分为1，并表示该方向被采样的相对概率。我们有上一本书中的一种方法，可以在一个单位的球体中取均匀的随机样本：

vec3 random_in_unit_sphere() {vec3 p;do {p = 2.0*vec3(myRandom(), myRandom(), myRandom()) - vec3(1, 1, 1);} while (dot(p, p) >= 1.0);return p;
}

为了得到单位球面上的点，我们可以将向量规格化为这些点：

vec3 random_in_unit_sphere() {vec3 p;do {p = 2.0*vec3(myRandom(), myRandom(), myRandom()) - vec3(1, 1, 1);} while (dot(p, p) >= 1.0);return unitVector(p);
}

现在这些统一的点的pdf是什么？作为单位球体上的密度，它是球体的1/面积或1/(4*Pi)。如果被积函数是cos^2(θ)，θ是与z轴的夹角：

#include <math.h>
#include <stdlib.h>
#include <stdio.h>
#include "time.h"
#include "Vec3.h"#define M_PI 3.14159265double myRandom() {return rand() / (RAND_MAX + 1.0);
}vec3 random_in_unit_sphere() {vec3 p;do {p = 2.0*vec3(myRandom(), myRandom(), myRandom()) - vec3(1, 1, 1);} while (dot(p, p) >= 1.0);return unitVector(p);
}inline float pdf(const vec3&p) {return 1 / (4 * M_PI);
}int main() {srand(time(NULL));int N = 1000000;float sum = 0.0;for (int i = 0;i < N;i++) {vec3 d = random_in_unit_sphere();float cosine_squared = d.z()*d.z();sum += cosine_squared / pdf(d);}printf("I = %f \n", sum/N);system("pause");
}

得到结果：

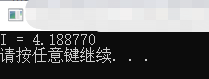
分析答案（如果你还记得足够的高级计算，请检查我！）是（4/3）*Pi，上面的代码生成这个值。接下来，我们准备将其应用于光线跟踪！

这里的关键点是所有的积分和概率，以及所有在单位球面上的积分和概率。单位球面上的面积是如何测量方向的。称之为方向，立体角，或面积-都是一样的。立体角是常用的术语。如果你对它的理解感到很舒服，那就太好了！但如果不是，做我所做的，想象单位球面上一组方向通过的区域。立体角ω和单位球面上的投影面积A是一样的。