本文主要是介绍BPMN建模示例,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
背景
对BPMN已经有了初步的了解,并且已经理解了BPMNJS这种流程引擎的工具,那么接下来我们已具体的案例来感性认知BPMN的能力,为接下来BPMN的学习做个铺垫。
是的,我们需要一个通俗易懂的例子,于是乎,我在网上找了一个,一个工单,物业维修流程的例子。
业务场景
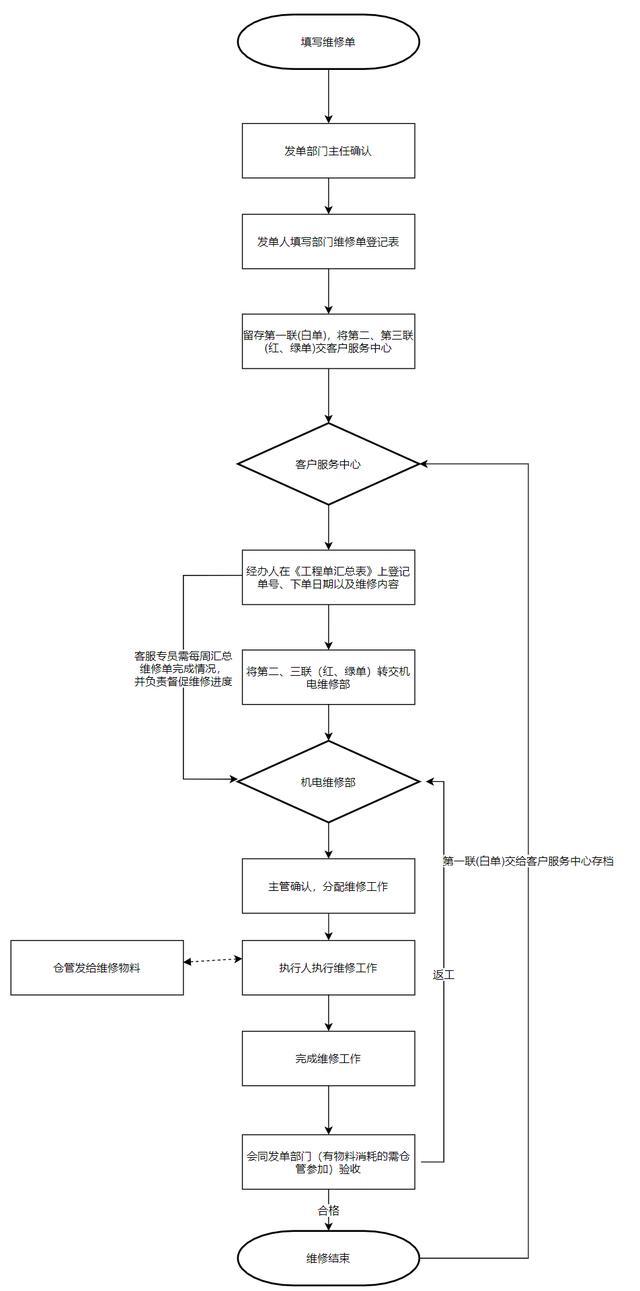
这是一个典型的物业维修流程。我们需要先建立一个战略层面上的流程,为什么需要比较高层(High-level)的流程呢?
业务还原
上面的例子,当我们使用业务分析的方法,去还原业务时,我们会发现现实是这样的:
客户参会人员:
- 我们的维修流程并不总是这样从业主填写维修单开始的,业主也可能是电话报修;
- 如果维修的工程量比较大的话,我们还得先提出方案,然后交给公司领导审批;
- 如果过了保修期的话,那我们还要收钱的;
- 业主如果是预约的话,我们还得根据他预约时间安排工作;
- 并不一定是业主报修,也可能是在物业巡检的时候发现问题,由巡检员报修。
- ……….
我们的BA,产品经理,或者项目经理估计很快就会崩溃,这也是我们常见的为何工作中能画出极其复杂的流程的原因。
这是画high-level流程的基本原因,从宏观看,方式迷失在细节,引入使用一些概念
- 泳池 泳道
- 任务 子流程
- 网关
- 事件
这些概念,需要分别一一的进行详细的拆解和学习

具体建模
和业务人员一起,把所有业务场景进行分解,然后使用BPMN建模如下:
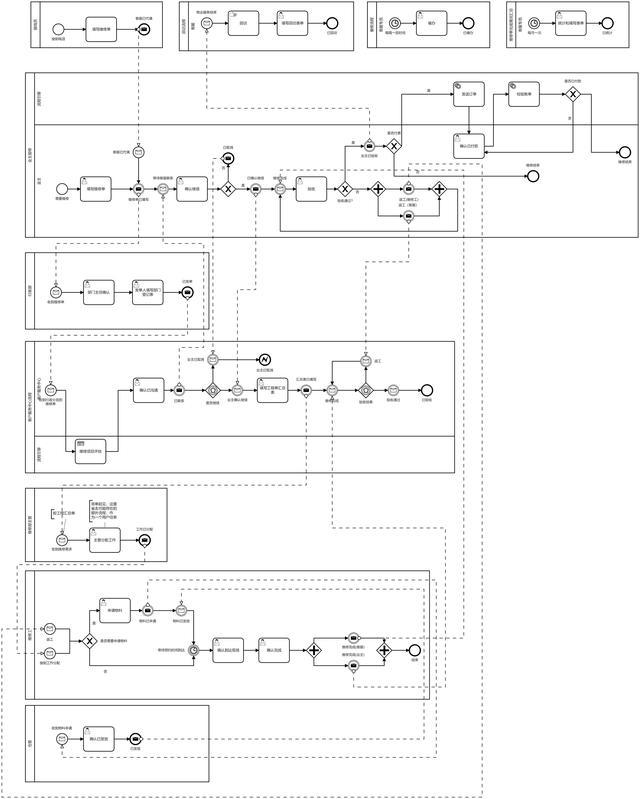
各个泳道,看不清,是的,我也没有看清的版本,也没有表要看清,看清了你可能很多地方也理解不了,就是根据业务规则的细化分解,到了具体的操作流程,不同的条件下,网关的路由(这个时候可能你对网关也是比较晕的概念),就是这样一张图,如果交给实施,开发,另外如果还出现新的业务变更,加上统计分析,是不是各种崩溃。
大问题
上面的业务场景,随着业务的梳理,面临着比较大的问题,就是一个大流程,还是分解为多个小流程,现实生活中由于受到技术和能力的限制,经常会碰到这样的问题,高耦合还是低耦合,类似于微服务带来的好处同时,坏处也是大大的,利弊如下:
分解流程的优点:
- 一个庞大的模型,它的版本迁移过程往往非常复杂,如果将它进行恰当的分解,那么我们只需要对发生了变动的部分进行迁移即可,可以有效的降低迁移成本。
- 对于开发者来说,庞大的或者过于复杂的模型会导致理解和开发成本迅速上升,而且一个单体模型,几乎只能由一个开发者来负责,不适合多人协作;而分解的手段可以将一个单体复杂模型分解成多个简单、可独立开发的流程模型,可以提升开发效率和降低理解难度。
- 对于企业工作流来说,多个工作流之间经常会存在共通的部分,就像这里的物业服务的回访流程,将这些公共部分剥离出来;长远来看,可以提升模型的复用率,从而提升开发效率。
缺点:
- 分解到什么程度并不那么容易把握,虽然按照经验来说往往是分解到每一个流程参与者,但在有些时候也可以将一些任务比较简单的参与者流程进行合并。
- 为了实现流程实例之间的通信,往往会存在较多的消息/信号事件或者调用活动,要求开发者对BPMN中的事件有足够的了解。
- 流程走向的观测可能会比较繁琐,因为需要在多个流程实例之间来回切换观察。
总结
由于是一篇感性认知篇,以上的业务场景由于并没有很深入业务细节、表单部分、还有统计等等,一个业务线可以拆解为几十个业务线,所以BPMN为何搞得那么繁琐,几百页的规范是有原因的,毕竟是为了从底层落地用的,当然,如何用最少的元素再抽象再去平衡,是非常考验产品经理和技术经理能力的。
这篇关于BPMN建模示例的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





