本文主要是介绍04-Gradient Descent,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
我们上一篇文章讲了线性回归算法, 并且我们提到了一种解析式的求模型参数的方法——最小二乘法, 但是该方法具有局限性,我们使用该方法的前提要求是我们输入的特征矩阵必须是可逆的, 但很有可能我们的矩阵不是可逆的, 那么这时我们就无法使用最小二乘法了 。而且使用最小二乘法也需要满足我们的拟合函数是线性的, 如果我们的拟合函数不是线性的, 我们就需要通过一些技巧转化为线性才可以使用。所以仅用最小二乘法求解模型参数是完全不够的, 那么本章就将介绍一种新的优化损失函数的工具——梯度下降法(Gradient Descent)
梯度下降法(Gradient Descent)
梯度下降常用于求解无约束条件下凸函数(Convex Function)的极小值。梯度下降法是一种迭代类型的算法,因为凸函数只有一个极值点,故求解出来的极小值点就是函数的最小值点。而有约束条件的情况下, 我们则可以用拉格朗日乘子法将约束最优化的目标函数转化为无约束条件下的目标函数, 然后进行梯度搜索。
J ( θ ) = 1 2 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2 θ ∗ = arg min θ J ( θ ) \begin{aligned} & J(\theta)=\frac{1}{2 m} \sum_{i=1}^m\left(h_\theta\left(x^{(i)}\right)-y^{(i)}\right)^2 \\ & \theta^*=\underset{\theta}{\arg \min } J(\theta) \end{aligned} J(θ)=2m1i=1∑m(hθ(x(i))−y(i))2θ∗=θargminJ(θ)
梯度其实就是对多个模型参数求偏导的结果所组成的一个向量
我们知道函数的导数对应的方向是该函数上升的方向, 而在损失函数中, 我们希望损失尽可能的小, 所以我们要想使损失降低就要找到损失降低的方向进行搜索, 直至找到一个最优的参数解。
如果某个函数不是严格的凸函数, 那么我们在使用梯度下降求极小值时, 求得的很可能是局部最优解, 而非全局最优解。
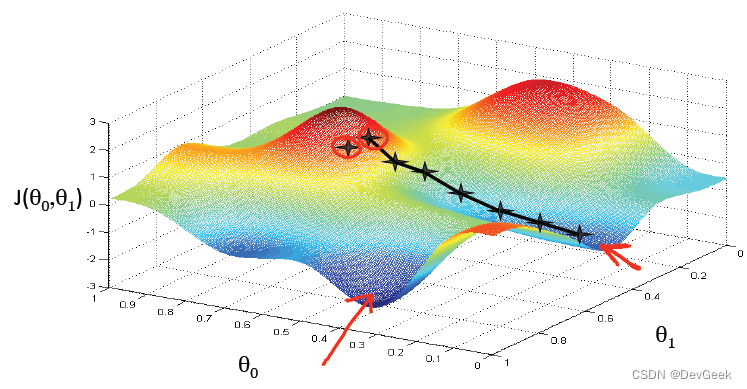
比如下图中梯度下降法在参数更新后得到了一个局部最优解(黑色轨迹), 原因是因为初始参数的选取不当。
梯度下降算法
步骤:
- 目标函数 θ \theta θ 求解 J ( θ ) = 1 2 ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2 J(\theta)=\frac{1}{2} \sum_{i=1}^m\left(h_\theta\left(x^{(i)}\right)-y^{(i)}\right)^2 J(θ)=21∑i=1m(hθ(x(i))−y(i))2
- 初始化 θ \theta θ (随机初始化,可以初始为 0 )
- 沿着负梯度方向迭代,更新后的 θ \theta θ 使 J ( θ ) J(\theta) J(θ) 更小
θ = θ − α ∙ ∂ J ( θ ) ∂ θ \theta=\theta-\alpha \bullet \frac{\partial J(\theta)}{\partial \theta} θ=θ−α∙∂θ∂J(θ)
- α \alpha α :学习率、步长
由于梯度下降法中负梯度方向作为变量的变化方向,所以有可能导致最终求解的值是局部最优解,所以在使用梯度下降的时候,一般需要进行一些调优策略:
- 学习率的选择:学习率过大,表示每次迭代更新的时候变化比较大,有可能会跳过最优解;学习率过小,表示每次迭代更新的时候变化比较小,就会导致迭代速度过慢,很长时间都不能结束;
- 算法初始参数值的选择:初始值不同,最终获得的最小值也有可能不同,因为梯度下降法求解的是局部最优解,所以一般情况下,选择多次不同初始值运行算法,并最终返回损失函数最小情况下的结果值;
- 标准化:由于样本不同特征的取值范围不同,可能会导致在各个不同参数上迭代速度不同,为了减少特征取值的影响,可以将特征进行标准化操作。
梯度方向
仅考虑单个样本的单个 θ \theta θ 参数的梯度值
J ( θ ) = 1 2 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2 ∂ ∂ θ j J ( θ ) = ∂ ∂ θ j 1 2 ( h θ ( x ) − y ) 2 = 2 ⋅ 1 2 ( h θ ( x ) − y ) ⋅ ∂ ∂ θ j ( h θ ( x ) − y ) = ( h θ ( x ) − y ) ∂ ∂ θ j ( ∑ i = 0 n θ i x i − y ) = ( h θ ( x ) − y ) x j \begin{aligned} &J(\theta)=\frac{1}{2 m} \sum_{i=1}^m\left(h_\theta\left(x^{(i)}\right)-y^{(i)}\right)^2 \\\frac{\partial}{\partial \theta_j} J(\theta) & =\frac{\partial}{\partial \theta_j} \frac{1}{2}\left(h_\theta(x)-y\right)^2 \\ & =2 \cdot \frac{1}{2}\left(h_\theta(x)-y\right) \cdot \frac{\partial}{\partial \theta_j}\left(h_\theta(x)-y\right) \\ & =\left(h_\theta(x)-y\right) \frac{\partial}{\partial \theta_j}\left(\sum_{i=0}^n \theta_i x_i-y\right) \\ & =\left(h_\theta(x)-y\right) x_j \end{aligned} ∂θj∂J(θ)J(θ)=2m1i=1∑m(hθ(x(i))−y(i))2=∂θj∂21(hθ(x)−y)2=2⋅21(hθ(x)−y)⋅∂θj∂(hθ(x)−y)=(hθ(x)−y)∂θj∂(i=0∑nθixi−y)=(hθ(x)−y)xj
梯度下降案例代码
import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt
import math
from mpl_toolkits.mplot3d import Axes3D
# 设置在jupyter中matplotlib的显示情况(表示不是嵌入显示)
# %matplotlib inline # 默认嵌入到jupyter中显示
%matplotlib tk
# 解决中文显示问题
mpl.rcParams['font.sans-serif'] = [u'SimHei']
mpl.rcParams['axes.unicode_minus'] = False
# 一维原始图像
def f1(x):return 0.5 * (x - 0.25) ** 2def df(x):return x - 0.25# 使用梯度下降法求解
GD_X = []
GD_y = []
x = 4 # 初始化x
alpha = 1.5 # 步长越小, 迭代次数越多
f1_change = f1(x)
f1_current = f1_change
GD_X.append(x)
GD_y.append(f1_current)
iter_num = 1while f1_change > 1e-10 and iter_num < 100: # 停止迭代的条件损失函数前后变化的差值小于1e-10或者迭代次数大于等于100次dx = df(x)x = x - alpha * dxtmp = f1(x)f1_change = np.abs(tmp - f1_current)f1_current = tmpGD_X.append(x)GD_y.append(f1_current)iter_num+=1print(u"最终结果为:(%.5f, %.5f)" % (x, f1_current))
print(u"迭代过程中X的取值,迭代次数:%d" % iter_num)
print(GD_X)# 构建数据
X = np.arange(-5, 5, 0.01)
Y = np.array(list(map(lambda t: f1(t), X)))# 绘图
plt.figure(facecolor='w')
plt.plot(X, Y, c='b', linestyle='solid', linewidth=2)
plt.plot(GD_X, GD_y, '.-', color='r')
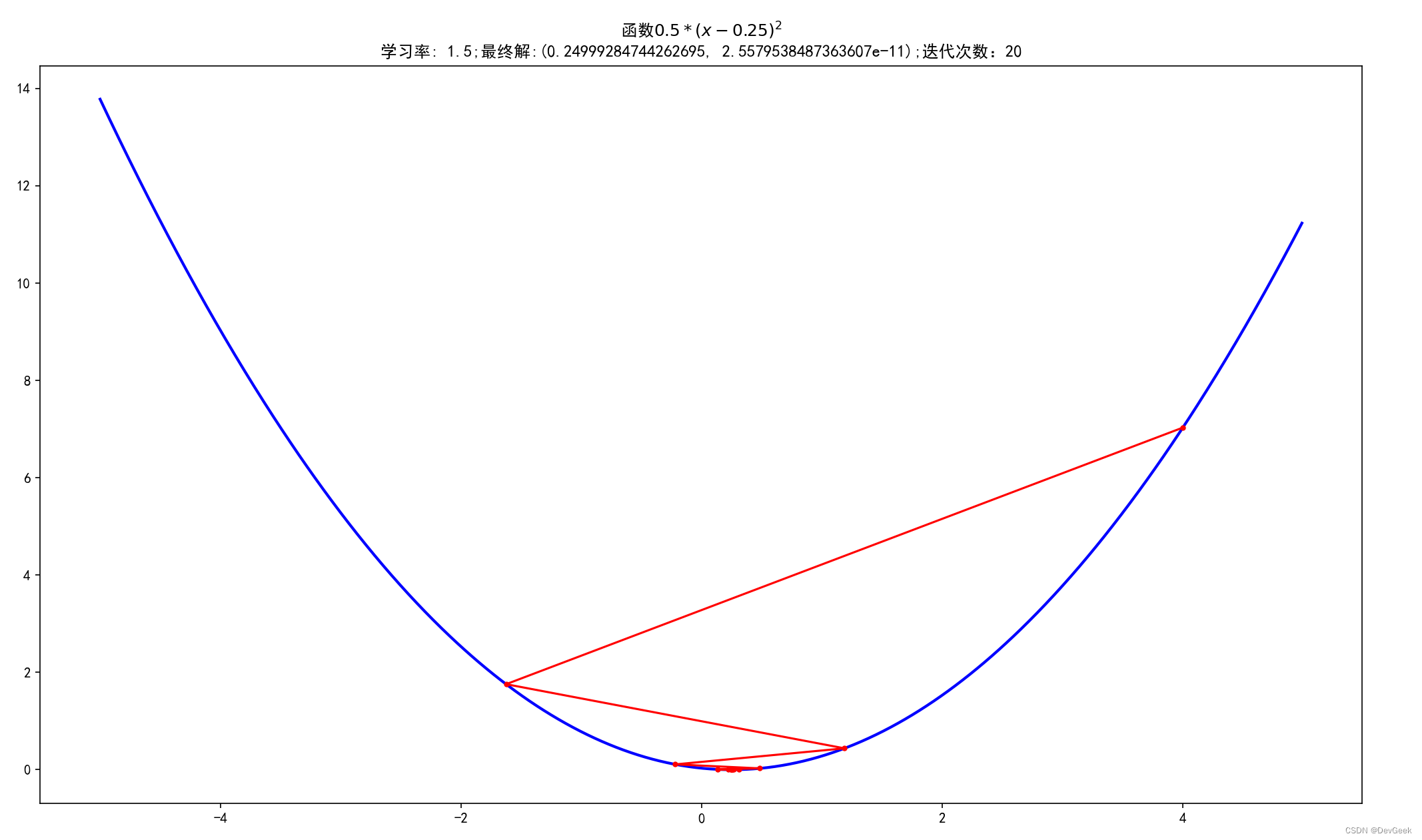
plt.title(f'函数$0.5 * (x - 0.25)^2$\n学习率: {alpha};最终解:{(x, f1_current)};迭代次数:{iter_num}')
plt.show()
最终结果为:(0.24999, 0.00000)
迭代过程中X的取值,迭代次数:20
[4, -1.625, 1.1875, -0.21875, 0.484375, 0.1328125, 0.30859375, 0.220703125, 0.2646484375, 0.24267578125, 0.253662109375, 0.2481689453125, 0.25091552734375, 0.249542236328125, 0.2502288818359375, 0.24988555908203125, 0.2500572204589844, 0.2499713897705078, 0.2500143051147461, 0.24999284744262695]
# 二维原始图像
def f2(x, y):return 0.6 * (x + y) ** 2 - x * ydef dfx(x, y):return 0.6 * (x + y) * 2 - ydef dfy(x, y):return 0.6 * (x + y) * 2 - x# 使用梯度下降法求解
GD_X2 = []
GD_y2 = []
GD_z2 = []
x2 = 4 # 初始化x2
y2 = 4 # 初始化y2
alpha2 = 0.01 # 步长越小, 迭代次数越多
f2_change = f2(x2, y2)
f2_current = f2_change
GD_X2.append(x2)
GD_y2.append(y2)
GD_z2.append(f2_current)
iter_num = 1while f2_change > 1e-8 and iter_num < 10000: # 停止迭代的条件损失函数前后变化的差值小于1e-10或者迭代次数大于等于100次dx = dfx(x2, y2)dy = dfy(x2, y2)x2 = x2 - alpha2 * dxy2 = y2 - alpha2 * dytmp = f2(x2, y2)f2_change = np.abs(tmp - f2_current)f2_current = tmpGD_X2.append(x2)GD_y2.append(y2)GD_z2.append(f2_current)iter_num+=1print(u"最终结果为:(%.5f, %.5f)" % (x2, f2_current))
print(u"迭代过程中X的取值,迭代次数:%d" % iter_num)
print(GD_X)# 构建数据
x = np.arange(-4, 4.5, 0.05)
y = np.arange(-4, 4.5, 0.05)
x, y = np.meshgrid(x, y)
z = np.array(list(map(lambda t: f2(t[0], t[1]), zip(x.flatten(), y.flatten()))))
z.shape = x.shapefig = plt.figure(facecolor='w', figsize=(15, 10))
ax = fig.add_subplot(111, projection='3d')
ax.plot_surface(x, y, z, rstride=1, cstride=1, cmap=plt.cm.jet)
ax.plot3D(GD_X2, GD_y2, GD_z2,linestyle='-.', c='r', marker='p', markersize=10, markerfacecolor='w')
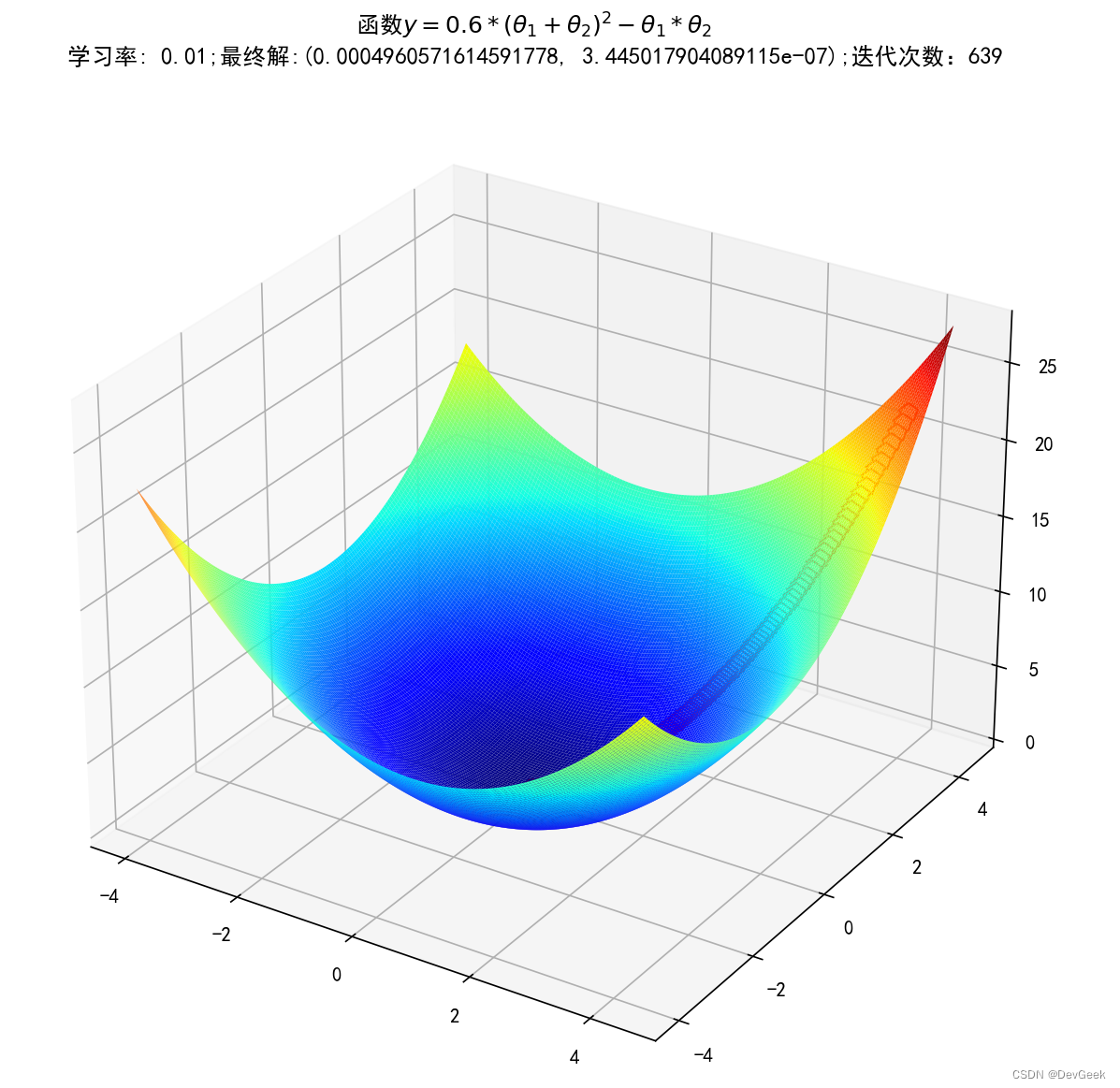
ax.set_title(f'函数$y=0.6 * (θ_1 + θ_2)^2 - θ_1 * θ_2$ \n学习率: {alpha2};最终解:{(x2, f2_current)};迭代次数:{iter_num}')
plt.show()
最终结果为:(0.00050, 0.00000)
迭代过程中X的取值,迭代次数:639
[4, -1.625, 1.1875, -0.21875, 0.484375, 0.1328125, 0.30859375, 0.220703125, 0.2646484375, 0.24267578125, 0.253662109375, 0.2481689453125, 0.25091552734375, 0.249542236328125, 0.2502288818359375, 0.24988555908203125, 0.2500572204589844, 0.2499713897705078, 0.2500143051147461, 0.24999284744262695]
随机梯度下降算法(SGD)
使用单个样本的梯度值作为当前模型参数 θ \theta θ 的更新
J ( θ ) = 1 2 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2 ∂ ∂ θ j J ( θ ) = ( h θ ( x ) − y ) x j for i = 1 to m , { θ j = θ j + α ( y ( i ) − h θ ( x ( i ) ) ) x j ( i ) } \begin{aligned} &J(\theta)=\frac{1}{2 m} \sum_{i=1}^m\left(h_\theta\left(x^{(i)}\right)-y^{(i)}\right)^2 \\\\ & \frac{\partial}{\partial \theta_j} J(\theta)=\left(h_\theta(x)-y\right) x_j \\ & \text { for } \mathrm{i}=1 \text { to } \mathrm{m},\{ \\ & \quad \theta_j=\theta_j+\alpha\left(y^{(i)}-h_\theta\left(x^{(i)}\right)\right) x_j^{(i)} \\ & \text { \}} \end{aligned} J(θ)=2m1i=1∑m(hθ(x(i))−y(i))2∂θj∂J(θ)=(hθ(x)−y)xj for i=1 to m,{θj=θj+α(y(i)−hθ(x(i)))xj(i) }
批量梯度下降算法(BGD)
使用所有样本的梯度值作为当前模型参数 θ \theta θ 的更新
∂ ∂ θ j J ( θ ) = ( h θ ( x ) − y ) x j ∂ J ( θ ) ∂ θ j = ∑ i = 1 m ∂ ∂ θ j = ∑ i = 1 m ( x j ( i ) ( h θ ( x ( i ) ) − y ( i ) ) ) = ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) x j ( i ) θ j = θ j + α ∑ i = 1 m ( y ( i ) − h θ ( x ( i ) ) ) x j ( i ) \begin{aligned} & \frac{\partial}{\partial \theta_j} J(\theta)=\left(h_\theta(x)-y\right) x_j \\ & \frac{\partial J(\theta)}{\partial \theta_j}=\sum_{i=1}^m \frac{\partial}{\partial \theta_j}=\sum_{i=1}^m\left(x_j^{(i)}\left(h_\theta\left(x^{(i)}\right)-y^{(i)}\right)\right)=\sum_{i=1}^m\left(h_\theta\left(x^{(i)}\right)-y^{(i)}\right) x_j^{(i)} \\ & \theta_j=\theta_j+\alpha \sum_{i=1}^m\left(y^{(i)}-h_\theta\left(x^{(i)}\right)\right) x_j^{(i)} \end{aligned} ∂θj∂J(θ)=(hθ(x)−y)xj∂θj∂J(θ)=i=1∑m∂θj∂=i=1∑m(xj(i)(hθ(x(i))−y(i)))=i=1∑m(hθ(x(i))−y(i))xj(i)θj=θj+αi=1∑m(y(i)−hθ(x(i)))xj(i)
小批量梯度下降法(MBGD)
如果即需要保证算法的训练过程比较快,又需要保证最终参数训练的准确率,而这正是小批量梯度下降法 (Mini-batch Gradient Descent,简称 MBGD) 的初衰。MBGD中不是每拿一个样本就更新一次梯度,而且拿b 个样本 ( b b b 一般为 10 )的平均梯度作为更新方向。
for i = 1 i=1 i=1 to m / 10 , { m / 10,\{ m/10,{
θ j = θ j + α ∑ k = i i + 10 ( y ( k ) − h θ ( x ( k ) ) ) x j ( k ) \theta_j=\theta_j+\alpha \sum_{k=i}^{i+10}\left(y^{(k)}-h_\theta\left(x^{(k)}\right)\right) x_j^{(k)} θj=θj+αk=i∑i+10(y(k)−hθ(x(k)))xj(k)
BGD和SGD算法比较
- SGD的速度比BGD快(整个数据集从头到尾执行的迭代次数少)。
- SGD在某些情况下(全局存在多个相对最优解或者J(θ)不是一个二次函数)有可能跳出某些小的局部最优解,所以一般情况下不会比BGD差;SGD在收敛的位置会存在J(θ)函数波动的情况。
- BGD一定能够得到一个局部最优解(在线性回归模型中一定是得到一个全局最优解),而SGD由于随机性的存在可能导致最终结果比BGD差。
- 注意:优先选择SGD。
BGD、SGD、MBGD的区别
- 当样本量为m的时候,每次迭代:
- BGD算法中对于参数值更新一次,
- SGD算法中对于参数值更新m次,
- MBGD算法中对于参数值更新m/n次,
相对来讲SGD算法的更新速度最快;
- SGD算法中对于每个样本都需要更新参数值,当样本值不太正常的时候,就有可能会导致本次的参数更新会产生相反的影响,也就是说SGD算法的结果并不是完全收敛的,而是在收敛结果处波动的;
- SGD算法是每个样本都更新一次参数值,所以SGD算法特别适合样本数据量大的情况以及在线机器学习(Online ML)。
案例-BGD、SGD、MBGD的比较
# encoding=utf-8
import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt# 设置字符集,防止中文乱码
mpl.rcParams['font.sans-serif'] = ['simHei']
mpl.rcParams['axes.unicode_minus'] = False
# # 设置在jupyter中matplotlib的显示情况(表示不是嵌入显示)
%matplotlib tk
#创建训练数据集
#假设训练学习一个线性函数y = 2.33x
EXAMPLE_NUM = 100 #训练总数
BATCH_SIZE = 10 #mini_batch训练集大小
TRAIN_STEP = 150 #训练次数
LEARNING_RATE = 0.0001 #学习率
X_INPUT = np.arange(EXAMPLE_NUM) * 0.1 #生成输入数据X
Y_OUTPUT_CORRECT = 5 * X_INPUT #生成训练正确输出数据
# 构造训练的函数
def train_func(x, K):return x * K
# BGD
# 参数初始化
theta_BGD = 0.0
# 记录梯度下降迭代的过程中参数的变化, 用于后续作图
theta_BGD_RECORD = [0.0]
for step in range(TRAIN_STEP):sum_BGD = 0for index in range(len(X_INPUT)):sum_BGD += (train_func(X_INPUT[index], theta_BGD) - Y_OUTPUT_CORRECT[index]) * X_INPUT[index]theta_BGD -= LEARNING_RATE * sum_BGDtheta_BGD_RECORD.append(theta_BGD)print(len(theta_BGD_RECORD))
1501
# SGD
# 参数初始化
theta_SGD = 0.0
# 记录梯度下降迭代的过程中参数的变化, 用于后续作图
theta_SGD_RECORD = [0.0]
for step in range(TRAIN_STEP):sum_SGD = 0index = np.random.randint(len(X_INPUT))sum_SGD += (train_func(X_INPUT[index], theta_SGD) - Y_OUTPUT_CORRECT[index]) * X_INPUT[index]theta_SGD -= LEARNING_RATE * sum_SGDtheta_SGD_RECORD.append(theta_SGD)print(len(theta_SGD_RECORD))
1501
# MBGD
# 参数初始化
theta_MBGD = 0.0
# 记录梯度下降迭代的过程中参数的变化, 用于后续作图
theta_MBGD_RECORD = [0.0]
for step in range(TRAIN_STEP):sum_MBGD = 0index_start = np.random.randint(len(X_INPUT) - BATCH_SIZE)for index in range(index_start, index_start + BATCH_SIZE):sum_MBGD += (train_func(X_INPUT[index], theta_MBGD) - Y_OUTPUT_CORRECT[index]) * X_INPUT[index]theta_MBGD -= LEARNING_RATE * sum_MBGDtheta_MBGD_RECORD.append(theta_MBGD)print(len(theta_MBGD_RECORD))
1501
plt.plot(range(1501 ), theta_BGD_RECORD, label='BGD')
plt.plot(range(1501), theta_SGD_RECORD, label='SGD')
plt.plot(range(1501), theta_MBGD_RECORD, label='MBGD')
plt.xlabel('Step')
plt.ylabel('theta')
plt.legend(loc='lower right')
<matplotlib.legend.Legend at 0x24cc6fe70d0>
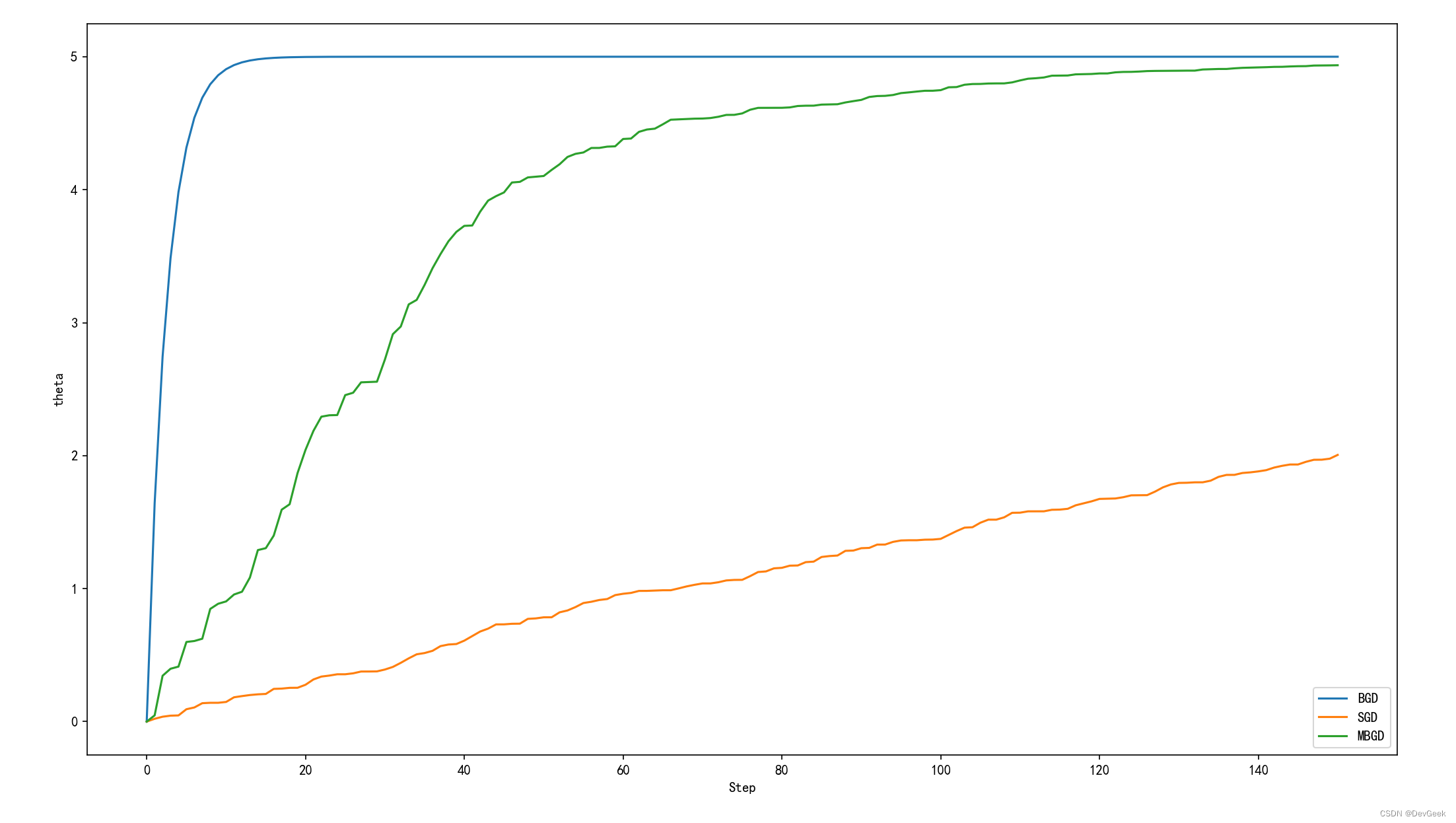
从图中我们首先可以看到SGD经过150次参数更新后并没有使损失函数达到最优解, 但MBGD和BGD最终都趋于实际参数5。
BGD在经过十多次迭代后就已趋近于最优解, 而MBGD经过一百四十多次的迭代后才趋近于实际的参数。那是不是就意味着BGD的速度快呢?从迭代次数上来说的确如此, 因为BGD收敛所需要的迭代次数更少, 但这不意味着BGD训练的时间最少, 因为BGD每次训练都要遍历一次所有的样本, 计算所有样本的梯度, 它虽然迭代了十几次就达到收敛, 但它实际上要计算上千次的梯度。图中的BGD每次迭代需计算所有样本的梯度, MBGD每次迭代需计算n个样本的梯度, SGD每次迭代仅需计算一个样本的梯度。
图中SGD在经过150次参数迭代更新后并没有使损失函数达到收敛, 这并不是说它收敛慢, 而是它收敛所需的次数比较多, 因为上面的案例中SGD计算梯度的次数最少。
另外我们从图中可以发现, bgd的所对应的曲线是一个光滑的曲线, 而SGD和MBGD是一个波动的曲线, 为什么会出现这种情况呢?
BGD使用整个训练数据集来更新模型的参数,而SGD和MBGD仅使用部分样本或单个样本来更新参数。在每次迭代中,BGD考虑了整个数据集的梯度信息,因此在相同迭代次数下,其更新方向比SGD和MBGD的每次迭代更加平均和稳定。这种更新的稳定性使得BGD的曲线呈现出更加光滑的趋势。
SGD和MBGD使用的是随机梯度估计,每次迭代只使用一个样本或少量样本来计算梯度。由于每个样本之间可能存在噪声或个别样本的梯度估计误差,因此SGD和MBGD的更新方向较为不稳定,会造成曲线在每次迭代中的波动。这种波动性使得SGD和MBGD的曲线在相同迭代次数下比BGD更加不光滑。
简单来说就是BGD在每次迭代中利用所有样本的信息来计算梯度并更新参数,因此其更新方向较为平均和稳定,使得曲线呈现更加光滑的趋势。而SGD和MBGD则使用部分样本的梯度估计和参数更新,导致更新方向较不稳定,使得曲线在每次迭代中产生较大的波动。
那么是不是使用BGD算法就是最好的选择呢?答案是否定的, 在我们的数据量大的情况下,BGD的计算量是巨大的且消耗的内存也是很大的, 所以在这个时候我们使用MBGD或者SGD可能会更好一些。
BGD、MBGD、SGD采用的都是迭代逼近的思想。
少量样本来计算梯度。由于每个样本之间可能存在噪声或个别样本的梯度估计误差,因此SGD和MBGD的更新方向较为不稳定,会造成曲线在每次迭代中的波动。这种波动性使得SGD和MBGD的曲线在相同迭代次数下比BGD更加不光滑。简单来说就是BGD在每次迭代中利用所有样本的信息来计算梯度并更新参数,因此其更新方向较为平均和稳定,使得曲线呈现更加光滑的趋势。而SGD和MBGD则使用部分样本的梯度估计和参数更新,导致更新方向较不稳定,使得曲线在每次迭代中产生较大的波动。
那么是不是使用BGD算法就是最好的选择呢?答案是否定的, 在我们的数据量大的情况下,BGD的计算量是巨大的且消耗的内存也是很大的, 所以在这个时候我们使用MBGD或者SGD可能会更好一些。
BGD、MBGD、SGD采用的都是迭代逼近的思想。
动手实现一个简单的梯度下降算法
为了进一步帮助大家理解梯度下降算法的工作原理, 接下来, 我们就动手来实现一个同时包含最小二乘法、BGD、MBGD、SGD求参方法的线性回归算法。
在本次实践中, 我们使用了r2_score回归性能度量指标, 为了加深理解, 我们不妨也将它一并实现出来。在日程的机器学习中, 我们经常使用scikit-learn这一机器学习库, 所以我们在习惯上更偏向于scikit-learn的算法实现风格。
我们将该算法封装在了本地的ML_master包下的metrics.py模块中
import numpy as npdef mean_squared_error(y_true, y_predict):"""计算y_true和y_predict之间的MSE"""assert len(y_true) == len(y_predict), \"the size of y_true must be equal to the size of y_predict"return np.sum((y_true - y_predict) ** 2) / len(y_predict)def r2_score(y_true, y_predict):"""计算y_train和y_predict之间的R Square"""return 1 - mean_squared_error(y_true, y_predict) / np.var(y_true)
接下来我们就正式开始实现我们的LinearRegression算法
我们将该算法封装在了本地的ML_master包下的LinearRegression.py模块中
import numpy as np
from ML_master.metrics import r2_scoreclass LinearRegression:def __init__(self):"""初始化LinearLinear Regression模型"""self.coef_ = Noneself.intercept_ = Noneself._theta = Nonedef fit_normal(self, X_train, y_train):"""根据训练数据集X_train, y_train训练Linear Regression模型"""assert X_train.shape[0] == y_train.shape[0], \"the size of X_train must be equal to the size of y_train"X_b = np.hstack([np.ones((len(X_train), 1)), X_train])self._theta = np.linalg.inv(X_b.T @ X_b) @ (X_b.T @ y_train)self.intercept_ = self._theta[0]self.coef_ = self._theta[1:]return selfdef fit_bgd(self, X_train, y_train, alpha=0.01, n_iters=1e4, epsilon=1e-8):"""根据训练数据集X_train, y_train使用梯度下降法训练Linear Regression模型"""assert X_train.shape[0] == y_train.shape[0], \'the size of X_train must be equal to the size of y_train'# 计算损失函数def j(theta, X_b, y):"""为了防止α值取得太大导致报错, 我们要设置异常处理机制"""try:return np.sum((X_b @ theta - y)) ** 2 / len(y)except RuntimeWarning:return float('inf')# 求偏导计算梯度def dj(theta, X_b, y):return X_b.T @ (X_b @ theta - y) * 2 / len(y)# 为了避免死循环的发生, 我们需要设置一个参数n_iters, 这个参数控制最大循环次数def gradient_descent(X_b, y, initial_theta):theta = initial_thetacur_iter = 0while cur_iter < n_iters:gradient = dj(theta, X_b, y)last_theta = thetatheta = last_theta - alpha * gradientif abs(j(last_theta, X_b, y) - j(theta, X_b, y)) < epsilon:breakcur_iter += 1return thetaX_b = np.hstack([np.ones((len(X_train), 1)), X_train])initial_theta = np.zeros(X_b.shape[1])self._theta = gradient_descent(X_b, y_train, initial_theta)self.intercept_ = self._theta[0]self.coef_ = self._theta[1:]return selfdef fit_mini_gd(self, X_train, y_train, n_iters=1e4, k=50, t0=5, t1=50):"""根据训练数据集X_train, y_train 使用小批量梯度下降法训练Linear Regression模型k: 每批次样本的数量t0、t1:: 多项式学习率动态衰减中, 我们手动设置的更新学习率的参数"""assert X_train.shape[0] == y_train.shape[0], \'the size of X_train must be equal to the size of y_train'assert n_iters >= 1, \'Traverse at least once'assert len(X_train) % k == 0, \'The number of samples in the X_train must be divisible by k'# 因为我们随机采用数据集中的一个样本的梯度的方向来更新参数, 所以我们不能够说沿着总体梯度下降的方向来更新参数def dj_mini_gd(theta, X_b_s, y_i_s):return X_b_s.T @ (X_b_s @ theta - y_i_s) * 2 / len(y_i_s)def mini_gd(X_b, y, initial_theta): # 在这里我们不需要传入学习率一塔了, 因为我们的一塔是动态变化的def learning_rate(t):"""t指的是迭代次数"""return t0 / (t + t1)theta = initial_thetam = len(X_b)# 总循环次数n_iters(遍历遍数) * 遍历一遍需要多少次循环(在这里我们的训练数据集中的样本是随机批量遍历的, 所以每次遍历数据集最少循环(m(样本数)/ 50)遍)for cur_iter in range(int(n_iters)):# 乱序后的索引shuffle_indexes = np.random.permutation(m)X_b_new = X_b[shuffle_indexes]y_new = y_train[shuffle_indexes]for i in range(int(m / k)):search_direction = dj_mini_gd(theta, X_b_new[i * k: (i + 1) * k], y_new[i * k: (i + 1) * k])theta = theta - learning_rate(cur_iter * (m / k) + i) * search_direction# 这条语句不再使用于我们的MBGD, 因为我们的损失函数的值并不能保证是一直在减小的, 损失函数的值的变化是跳跃的, 也正因为如此, 这条语句不适用于我们的随机梯度下降法,两次搜索的差距特别地小,并不代表离那个损失函数的极值点更近了,很有可能跟随机的样本得到的这个梯度有关。# if abs(j(theta, X_b, y) - j(last_theta, X_b, y)) < epsilon:# break# 此时我们的循环终止只有一个条件--循环次数return thetaX_b = np.hstack([np.ones((len(X_train), 1)), X_train])initial_theta = np.zeros(X_b.shape[1])self._theta = mini_gd(X_b, y_train, initial_theta)self.intercept_ = self._theta[0]self.coef_ = self._theta[1:]return selfdef fit_sgd(self, X_train, y_train, t0=5, t1=50, n_iters=1e4):"""根据训练数据集X_train, y_train, 使用梯度下降法训练Linear Regression模型"""assert X_train.shape[0] == y_train.shape[0], \"the size of X_train must be equal to the size of y_train"def dj_sgd(theta, X_b_i, y_i):"""X_b_i代表矩阵中随机的一个样本, y_i是该样本相对应的真实值"""return X_b_i * (X_b_i @ theta - y_i) * 2.def sgd(X_b, y, initial_theta): # 在这里我们不需要传入学习率一塔了, 因为我们的一塔是动态变化的def learning_rate(t):"""t指的是迭代次数"""return t0 / (t + t1)theta = initial_thetam = len(X_b)# 总循环次数n_iters(遍历遍数) * 遍历一遍至少需要多少次循环(在这里我们的训练数据集中的样本是随机进行遍历的, 所以每次遍历数据集最少也要循环m(样本数)遍)for cur_iter in range(int(n_iters)):# 乱序后的索引shuffle_indexes = np.random.permutation(m)X_b_new = X_b[shuffle_indexes]y_new = y_train[shuffle_indexes]for i in range(m):search_direction = dj_sgd(theta, X_b_new[i], y_new[i])theta = theta - learning_rate(cur_iter * m + i) * search_direction# 这条语句不再使用于我们的SGD, 因为我们的损失函数的值并不能保证是一直在减小的, 损失函数的值的变化是跳跃的, 也正因为如此, 这条语句不适用于我们的随机梯度下降法,两次搜索的差距特别地小,并不代表离那个损失函数的极值点更近了,很有可能跟随机的样本得到的这个梯度有关。# if abs(j(theta, X_b, y) - j(last_theta, X_b, y)) < epsilon:# break# 此时我们的循环终止只有一个条件--循环次数return thetaX_b = np.hstack([np.ones([len(X_train), 1]), X_train])initial_theta = np.zeros(X_b.shape[1])self._theta = sgd(X_b, y_train, initial_theta)self.intercept_ = self._theta[0]self.coef_ = self._theta[1:]return selfdef predict(self, X):assert self.intercept_ is not None and self.coef_ is not None, \"must fit before predict"assert X.shape[1] == len(self.coef_), \"the feature number of X_predict must be equal to X_train"X_b = np.hstack([np.ones((len(X), 1)), X])return X_b @ self._thetadef score(self, X_test, y_test):y_pred = self.predict(X_test)return r2_score(y_test, y_pred)def __repr__(self):return "LinearRegression()"在封装好我们的线性回归算法之后,为了便于我们后续的测试,我们要将数据按比例划分为训练和测试数据集, 这一过程显然少不了sklearn库中已经为我们封装好的train_test_split方法, 但是为了让大家更好地理解这一过程, 我们仍手动对train_test_split进行简单的实现。
我们将该算法封装在了本地的ML_master包下的model_selection.py模块中
# coding: utf-8import numpy as npdef train_test_split(X, y, test_ratio=0.2, seed=None):"""将数据集按照比例划分为训练集和测试集:param seed:随机生成器种子。在确定了种子之后,无论何时运行程序,使用随机函数(如random.random())生成的随机数序列都将是一样的。这意味着相同的种子将生成相同的随机数序列,因此可以确保结果的可复现性。这在我们进行debug的过程中是非常有用的, 它保证我们每次调用函数所产生的结果是一致的"""assert X.shape[0] == len(y), \'the size of X must be equal to the size of y'assert 0 < test_ratio < 1, \'test_ratio must be valid'if seed:np.random.seed(seed)shuffle_indexes = np.random.permutation(X.shape[0])test_size = int(test_ratio * len(X))test_indexes = shuffle_indexes[:test_size]train_indexes = shuffle_indexes[test_size:]X_train = X[train_indexes]X_test = X[test_indexes]y_train = y[train_indexes]y_test = y[test_indexes]return X_train, X_test, y_train, y_test
另外,对数据进行标准化或归一化也格外的重要, 它可以避免特征尺度不同而造成梯度下降过程中可能会遇到的收敛速度慢、收敛不稳定, 数据溢出等问题, 且归一化操作能够加快梯度下降的收敛。为了使大家更好地理解这一过程,我们也简单地实现一个标准化转换器(StandardScaler)
我们将该算法封装在了本地的ML_master包下的preprocessing.py模块中
import numpy as npclass StandardScaler:def __init__(self):self.mean_ = Noneself.scale_ = Nonedef fit(self, X_train):"""根据训练数据集来获得每一个特征的均值和标准差"""self.mean_ = np.mean(X_train, axis=0)self.scale_ = np.std(X_train, axis=0)def transform(self, X):"""对输入数据进行均值方差归一化"""assert self.mean_ is not None and self.scale_ is not None, \'must fit before transform'assert X.shape[1] == len(self.mean_), \'the size of X must be equal to mean_ and scale_'ResX = np.empty(X.shape, dtype=float)for col in range(X.shape[1]):ResX[:, col] = (X[:, col] - self.mean_[col]) / self.scale_[col]return ResX接下来我们新建一个main_LinearRegression来对我们封装好的算法进行一个测试。在这里我们使用波士顿房价数据集。
首先导入我们所需要的模块
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from ML_master.LinearRegression import LinearRegression
from ML_master.model_selection import train_test_split
from ML_master.preprocessing import StandardScaler
导入数据
names = ['CRIM', 'ZN', 'INDUS', 'CHAS', 'NOX', 'RM', 'GE', 'DIS', 'RAD', 'TAX', 'PRTATIO', 'B', 'LSTAT', 'PRICE']
data = pd.read_csv('datasets/housing-Sheet1.csv', header=None, names=names, delim_whitespace=True)
X = data.iloc[:, :-1]
y = data.iloc[:, -1]观察每个特征与目标变量之间的关系
fig = plt.figure(facecolor='w', figsize=(15, 15))
for col in range(X.shape[1]):plt.subplot(3, 5, col + 1)plt.scatter(X.iloc[:, [col]], y)plt.ylabel('PRICE')plt.xlabel(names[col])plt.title(names[col])plt.tight_layout(h_pad=3, w_pad=1)
plt.show()

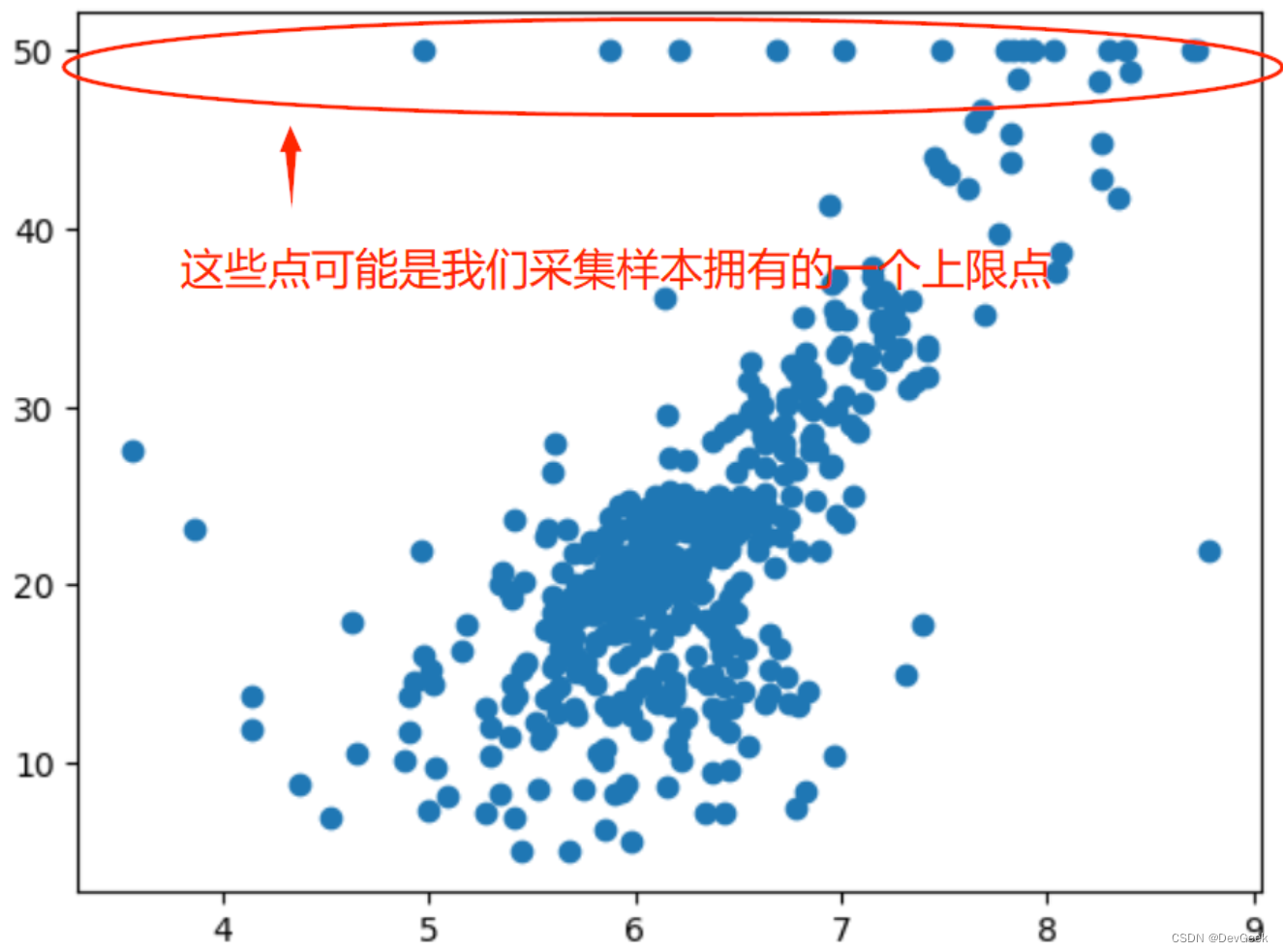
我们通过上图可以看到PRICE的上限是50万$,而有一些数据恰好在这个位置,看起来有些奇怪, 试试上我们俨然有可能在真实的世界中获得的数据也会是这个样子, 其实这些点是我们采集样本时的上限点, 换句话说有时候我们采集数据时, 由于各种原因, 比如计量仪器的最大值限制、问卷设置的最大值(超过某一范围的数据我们单独用一个选项统计),所以会定一个最大值。在上图中, 房价50万$显然就是我们设置的一个最大值,我们把房价大于等于50万美元的都视为了50万$。
对于这些采用最大值表示的点,显然它们很有可能不是真实的点, 所以这里我们只收集那些房价不超过50万美元的数据。
选取房价小于50万美元所对应的数据
X = np.array(X[y < 50])
y = np.array(y[y < 50])
将我们的数据集划分为训练集和测试集, 接着对数据进行标准化。
X_train, X_test, y_train, y_test = train_test_split(X, y, test_ratio=0.2, seed=666)standardScaler = StandardScaler()
standardScaler.fit(X_train)X_train_scaled = standardScaler.transform(X_train)
X_test_scaled = standardScaler.transform(X_test)
建立线性回归模型, 调用不同的拟合函数进行训练, 接着对测试集中的数据进行预测。
lr = LinearRegression()
lr.fit_normal(X_train_scaled, y_train)
print(lr.score(X_test_scaled, y_test))lr2 = LinearRegression()
lr2.fit_sgd(X_train_scaled, y_train)
print(lr2.score(X_train_scaled, y_train))lr3 = LinearRegression()
lr3.fit_mini_gd(X_train_scaled, y_train, k=8)
print(lr3.score(X_train_scaled, y_train))lr4 = LinearRegression()
lr4.fit_bgd(X_train_scaled, y_train)
print(lr4.score(X_train_scaled, y_train))返回每个模型的回归系数以及R方值
[-1.04081022 0.83158615 -0.24610116 0.01155073 -1.35071223 2.25043742-0.6635109 -2.53553062 2.26056108 -2.34552677 -1.76579278 0.709267-2.72690877]
0.8129794056212811 [-1.04070099 0.83141519 -0.24665086 0.01161779 -1.35064281 2.25049392-0.66359268 -2.5355954 2.25916843 -2.34396194 -1.76576001 0.70924793-2.72688652]
0.7672755256314215 [-1.04046596 0.83101361 -0.24777104 0.01176859 -1.35041867 2.25067236-0.66379492 -2.53569598 2.2562218 -2.34066192 -1.76567376 0.70922924-2.72679653]
0.7672754812462621 [-0.94269143 0.6619153 -0.53531899 0.04200301 -1.15333267 2.33593154-0.71376438 -2.3946628 1.40318902 -1.4496494 -1.73171823 0.70857997-2.70643919]
0.7653153288983956
这篇关于04-Gradient Descent的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





![[苍穹外卖]-04菜品管理接口开发](https://img-blog.csdnimg.cn/img_convert/4eb87ad3e530cfa9b1cd33c4976f527f.png)


