【智能优化算法】鹦鹉优化算法（Parrot optimizer，PO）

本文主要是介绍【智能优化算法】鹦鹉优化算法（Parrot optimizer，PO），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

Parrot optimizer（鹦鹉优化算法）是发表在中科院二区Computers in Biology and Medicine期刊上的论文“Parrot optimizer: Algorithm and applications to medical problems”

01.引言

随机优化方法作为一种有效的技术在当代研究中得到了显著的突出，有效地解决了复杂的优化挑战。本文介绍了鹦鹉优化器(Parrot Optimizer, PO)，这是一种基于训练后鹦鹉关键行为的高效优化方法。本研究以定性分析和综合实验为特色，展示了Parrot Optimizer在处理各种优化问题时的鲜明特点。性能评估包括对提议的PO在35个功能上进行基准测试，包括IEEE CEC 2022测试集的经典案例和问题，并将其与八种流行的算法进行比较。研究结果生动地突出了PO在探索性和开发性方面的竞争优势。此外，通过参数灵敏度实验探讨了所提出的PO在不同构型下的适应性。应用于工程设计问题，证明了该方法的有效性和优越性。为了进一步将评估扩展到现实世界的应用，我们将PO在疾病诊断和医学图像分割问题中的应用纳入其中，这些问题在医学领域中具有高度相关性和重要意义。总之，研究结果证明，PO是一种有前途和竞争力的算法，超越了文献中的一些现有算法。

02.文章的贡献

1.介绍鹦鹉优化器，一种适用于各种优化情况的高效优化器。

2. 构建高效优化机制的特点是没有明确划分勘探和开发阶段，但提高了优化能力。

3. 通过全面的定性分析和参数灵敏度实验，深入探索PO算法的特点，增强其在各种优化问题中的适用性。

4. 通过与8种常用算法的对比实验验证了该算法的性能，证明了该算法在解决各种优化挑战方面有很强竞争力。

5. 将PO算法应用于5个现实世界的优化问题，证实了它在解决广泛的实际优化任务方面的潜力。

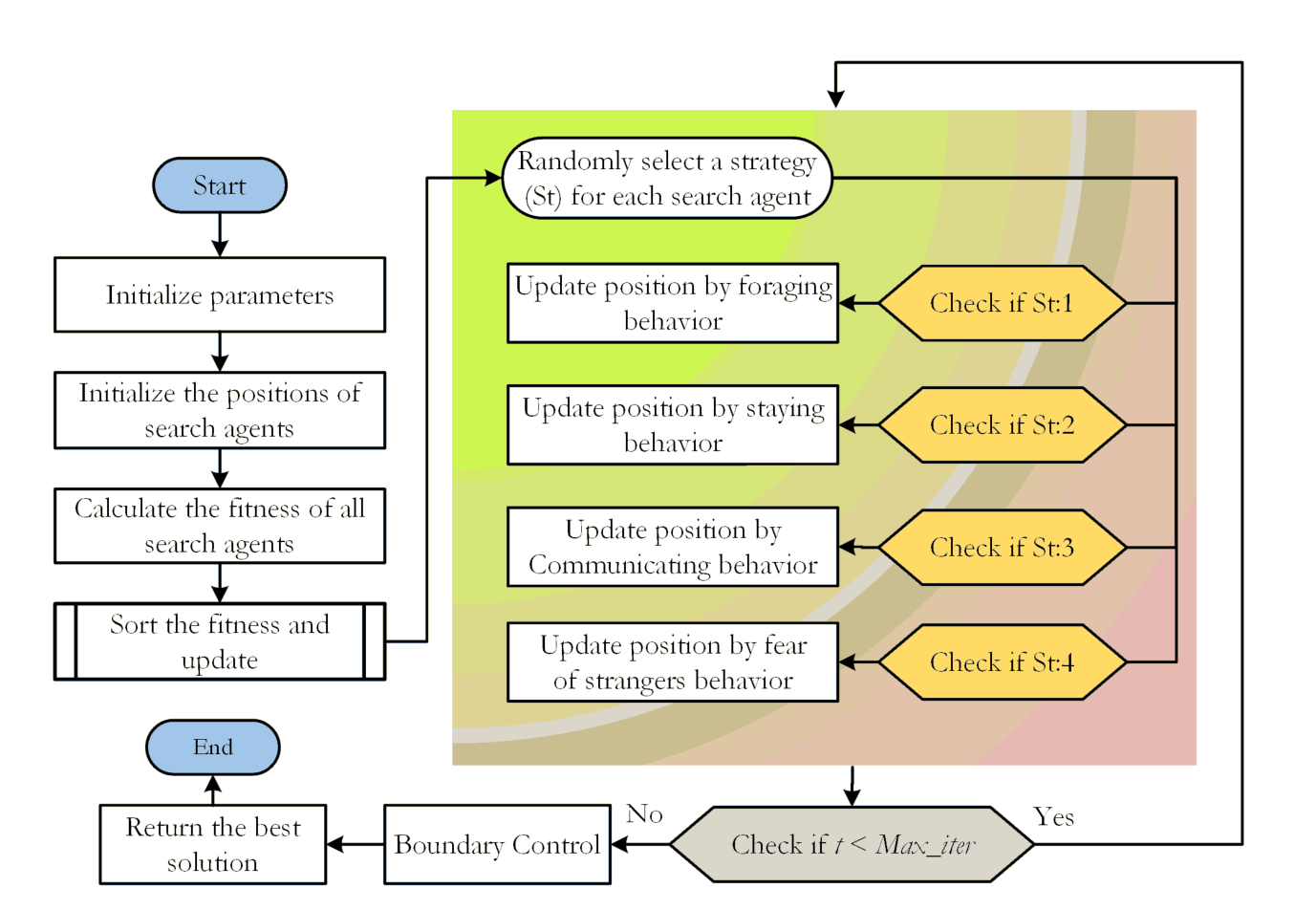
03.代码流程图

03.部分代码

%___________________________________________________________________________________________________________________________________________________%
% Parrot Optimizer (PO) source codes (version 1.0)
% PO
% Parrot optimizer: Algorithm and applications to medical problems
% Website and codes of Parrot optimizer(PO):http://www.aliasgharheidari.com/PO.html
% Junbo Lian, Guohua Hui, Ling Ma, Ting Zhu, Xincan Wu, Ali Asghar Heidari, Yi Chen, Huiling Chen
% Last update: Jan 31 2023
% E-Mail: as_heidari@ut.ac.ir, aliasghar68@gmail.com, chenhuiling.jlu@gmail.com %----------------------------------------------------------------------------------------------------------------------------------------------------%
% Authors: Junbo Lian (junbolian@qq.com), Ali Asghar Heidari(as_heidari@ut.ac.ir, aliasghar68@gmail.com), Huiling Chen(chenhuiling.jlu@gmail.com) 
%----------------------------------------------------------------------------------------------------------------------------------------------------%
function [avg_fitness_curve, Best_pos, Best_score, curve, search_history, fitness_history] = PO(N, Max_iter, lb, ub, dim, fobj)
% BestF: Best value in a certain iteration
% WorstF: Worst value in a certain iteration
% GBestF: Global best fitness value
% AveF: Average value in each iteration
if (max(size(ub)) == 1)ub = ub .* ones(1, dim);lb = lb .* ones(1, dim);
end
%% Initialization
X0 = initialization(N, dim, ub, lb); % Initialization
X = X0;
% Compute initial fitness values
fitness = zeros(1, N);
for i = 1:Nfitness(i) = fobj(X(i, :));
end
[fitness, index] = sort(fitness); % sort
GBestF = fitness(1); % Global best fitness value
AveF = mean(fitness);
for i = 1:NX(i, :) = X0(index(i), :);
end
curve = zeros(1, Max_iter);
avg_fitness_curve = zeros(1, Max_iter);
GBestX = X(1, :); % Global best position
X_new = X;
search_history = zeros(N, Max_iter, dim);
fitness_history = zeros(N, Max_iter);
%% Start search
for i = 1:Max_iterif mod(i,100) == 0display(['At iteration ', num2str(i), ' the fitness is ', num2str(curve(i-1))]);endavg_fitness_curve(i) = AveF;alpha = rand(1) / 5;sita = rand(1) * pi;for j = 1:size(X, 1)St = randi([1, 4]);% foraging behaviorif St == 1X_new(j, :) = (X(j, :) - GBestX) .* Levy(dim) + rand(1) * mean(X(j, :)) * (1 - i / Max_iter) ^ (2 * i / Max_iter);% staying behaviorelseif St == 2X_new(j, :) = X(j, :) + GBestX .* Levy(dim) + randn() * (1 - i / Max_iter) * ones(1, dim);% communicating behaviorelseif St == 3H = rand(1);if H < 0.5X_new(j, :) = X(j, :) + alpha * (1 - i / Max_iter) * (X(j, :) - mean(X(j, :)));elseX_new(j, :) = X(j, :) + alpha * (1 - i / Max_iter) * exp(-j / (rand(1) * Max_iter));end% fear of strangers' behaviorelseX_new(j, :) = X(j, :) + rand() * cos((pi *i )/ (2 * Max_iter)) * (GBestX - X(j, :)) - cos(sita) * (i / Max_iter) ^ (2 / Max_iter) * (X(j, :) - GBestX);end% Boundary controlfor j = 1:Nfor a = 1:dimif (X_new(j, a) > ub(a))X_new(j, a) = ub(a);endif (X_new(j, a) < lb(a))X_new(j, a) = lb(a);endendend% Update positionsfor j = 1:Nfitness_new(j) = fobj(X_new(j, :));endfor j = 1:Nif (fitness_new(j) < GBestF)GBestF = fitness_new(j);GBestX = X_new(j, :);endendX = X_new;fitness = fitness_new;% Sorting and updating[fitness, index] = sort(fitness); % sortfor j = 1:NX(j, :) = X(index(j), :);endcurve(i) = GBestF;endBest_pos = GBestX;Best_score = curve(end);search_history(:, i, :) = X;fitness_history(:, i) = fitness;
end
%%  Levy search strategy
function o = Levy(d)beta = 1.5;sigma = (gamma(1 + beta) *sin(pi * beta / 2) / (gamma((1 + beta) / 2) * beta * 2^((beta - 1) / 2)))^(1 / beta);u = randn(1, d) * sigma;v = randn(1, d);step = u ./ abs(v).^(1 / beta);o = step;
end   
end

04.代码效果图

默认PO算法保持觅食(F)、停留(S)、交流(C)、惧陌生人(O)行为的等比例，表示为1:1:1:1。然而，我们假设改变这些行为的分布可能会产生不同的优化结果。为了验证这一假设，我们设计了参数敏感性分析实验。建立了五种不同行为比的PO算法变体。其中包括原PO算法F:S:C:O = 1:1:1:1、PO-F算法F:S:C:O = 2:1:1:1、PO-S算法F:S:C:O = 1:2:1:1、PO-C算法F:S:C:O = 1:1:2、PO-O算法F:S:C:O = 1:1:2。在保持相同迭代次数和种群大小(如3.1节所述)的情况下，分别在经典测试函数集和IEEE CEC 2022测试集上对这五种不同参数的PO算法进行测试，研究参数敏感性。