本文主要是介绍【数据结构】考研真题攻克与重点知识点剖析 - 第 3 篇:栈、队列和数组,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
前言
- 本文基础知识部分来自于b站:分享笔记的好人儿的思维导图与王道考研课程,感谢大佬的开源精神,习题来自老师划的重点以及考研真题。
- 此前我尝试了完全使用Python或是结合大语言模型对考研真题进行数据清洗与可视化分析,本人技术有限,最终数据清洗结果不够理想,相关CSDN文章便没有发出。
(考研真题待更新)
欢迎订阅专栏:408直通车
请注意,本文中的部分内容来自网络搜集和个人实践,如有任何错误,请随时向我们提出批评和指正。本文仅供学习和交流使用,不涉及任何商业目的。如果因本文内容引发版权或侵权问题,请通过私信告知我们,我们将立即予以删除。
文章目录
- 前言
- 第三章 栈、队列和数组
- 栈
- 栈的概念
- 栈的实现
- 顺序栈
- S.top == 0
- 共享栈
- 链栈
- 队列
- 队列的概念
- 队列的实现
- 队列的顺序存储结构
- rear指向队尾元素
- 队列的链式存储结构
- 小结
- 双端队列(挺喜欢考的考点)
- 栈和队列有相同逻辑结构,线性结构
- 合适与不合适做链队的链表,关键看能不能获取到首尾指针(带首尾的非循环或带尾的循环)
- 栈和队列的应用
- 栈的应用
- 括号
- 表达式求值
- 中缀表达式转后缀表达式
- 后缀表达式的计算
- 中缀表达式转前缀表达式
- 前缀表达式的计算
- 中缀表达式的计算(用栈实现)
- 其他
- 小结
- 递归
- 小结
- 队列的应用
- 数组和特殊矩阵
- 本节的题目计算都可以不记公式,直接代入推导
- 数组
- 特殊矩阵
- 补充代码
- 栈(数组模拟)
- (循环)队列(数组模拟)
- 单调栈
- 单调队列
- 考研真题
- 408 - 2023
第三章 栈、队列和数组
栈

栈的概念
-
-
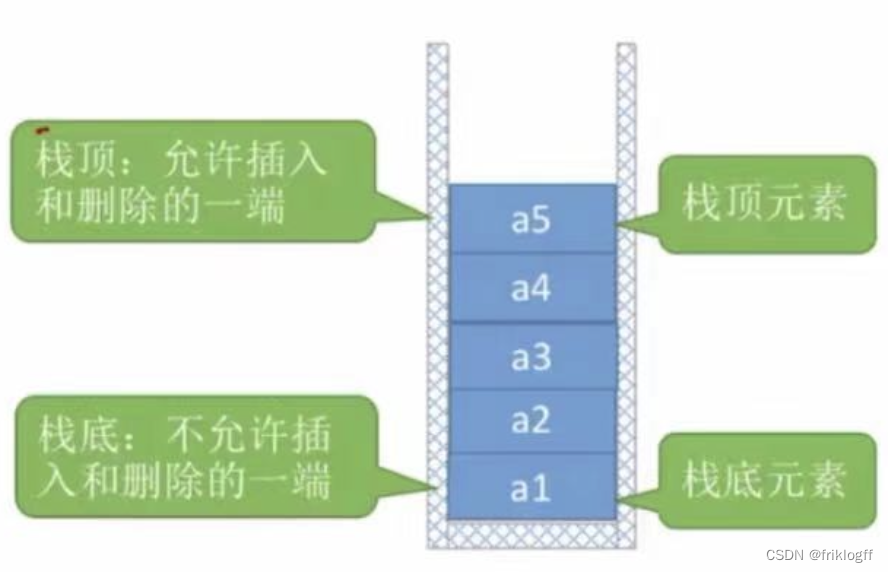
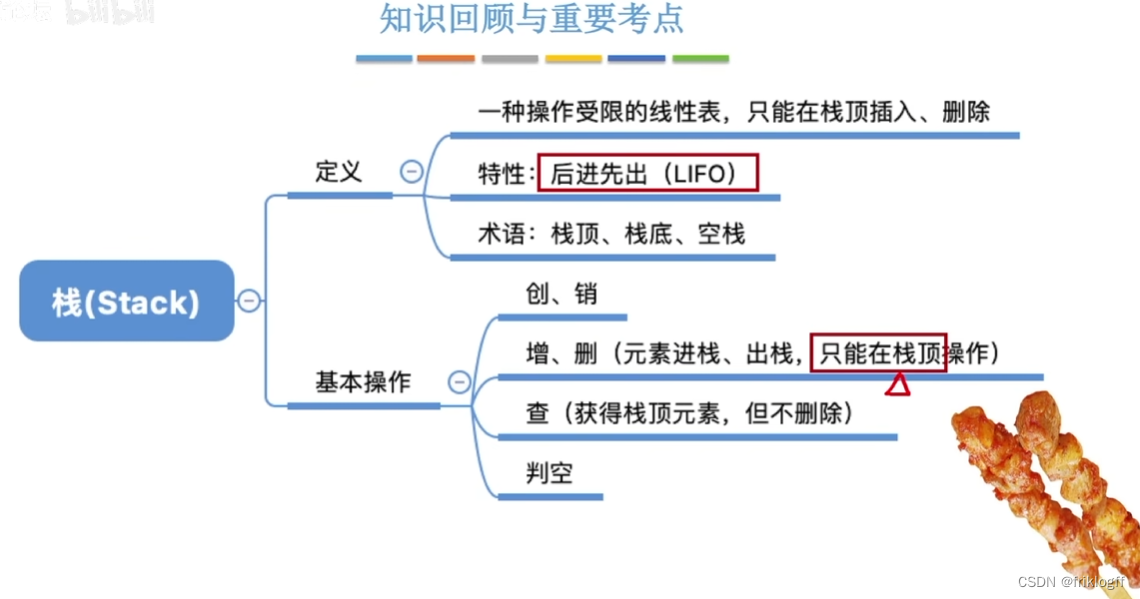
限定仅在一端进行插入和删除操作的线性表,又称后进先出(LIFO)的线性表;
允许插入删除的那一端叫栈顶(Top),不允许插入和删除的一端叫栈底(Bottom)- 特殊的线性表,后进先出(LIFO)
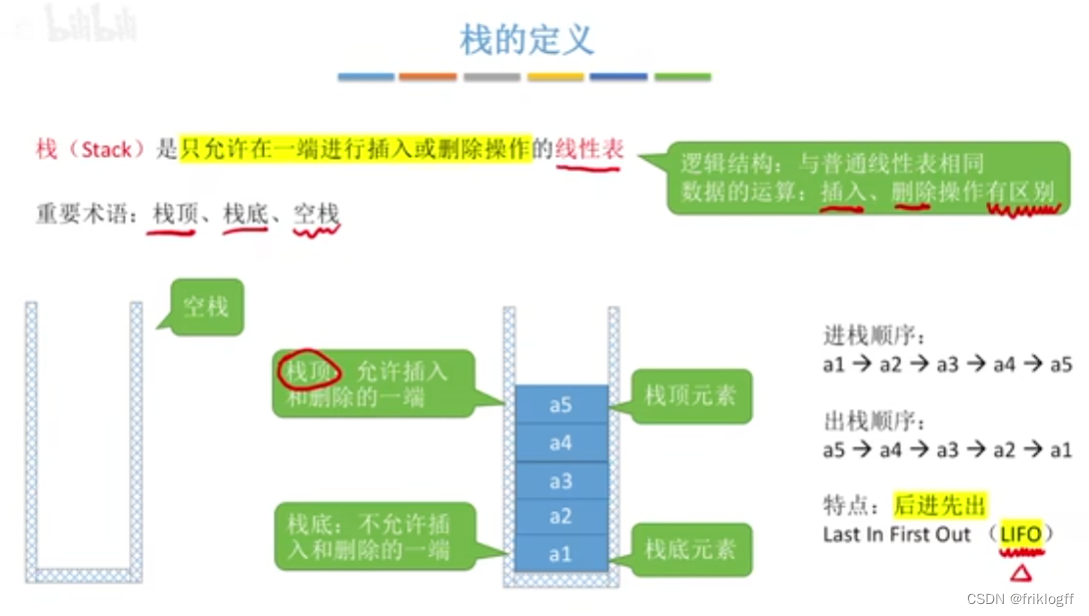
- 特殊的线性表,后进先出(LIFO)
-
注意:n个不同元素进栈,出栈元素不同排序个数为(n个元素能构成多少种不同的二叉树)
-

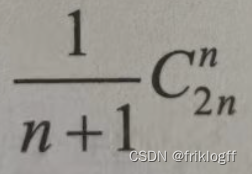
-
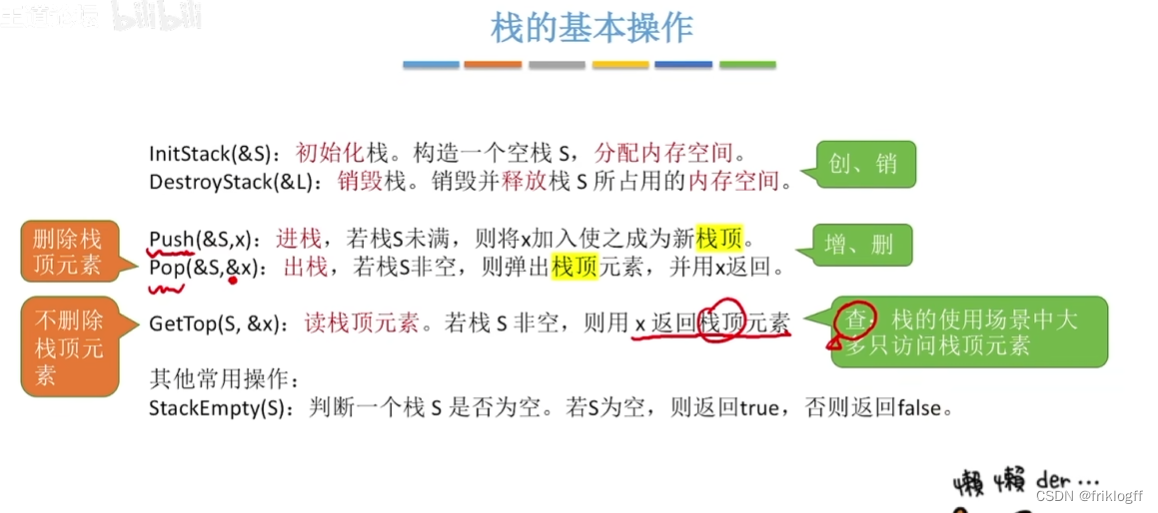
栈的实现
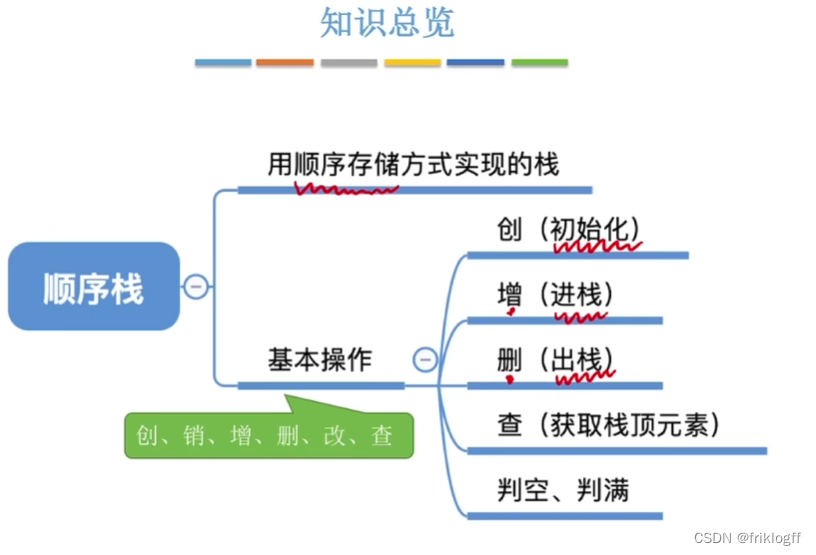
顺序栈
-
栈的顺序存储结构
-
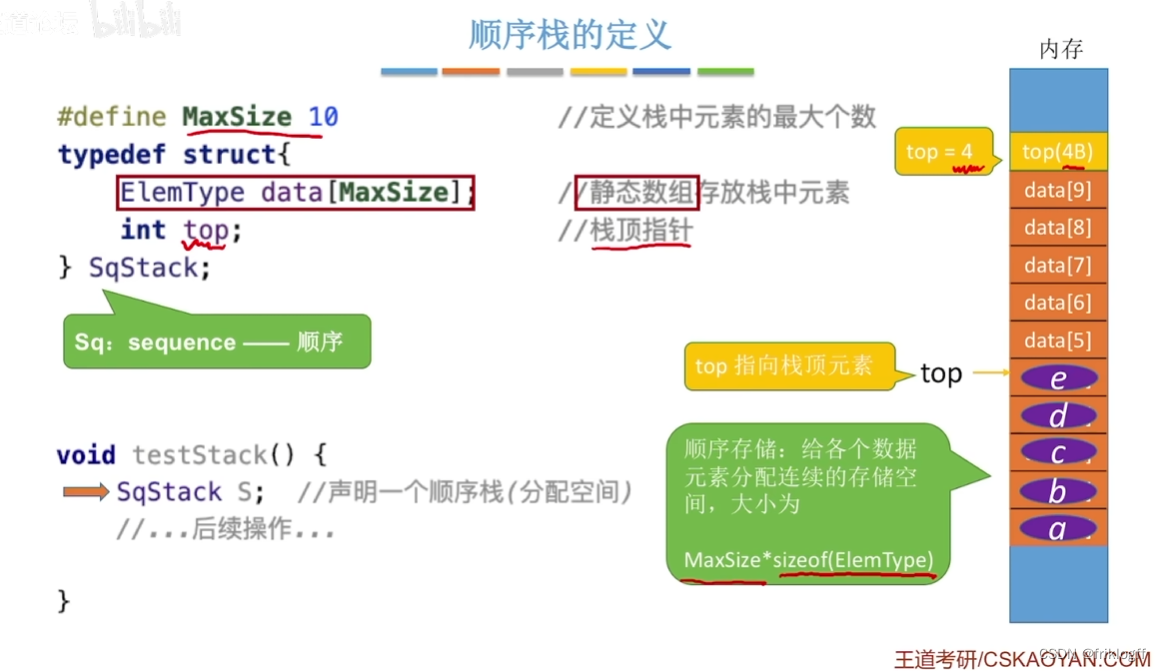
顺序栈的基本结构
-

-
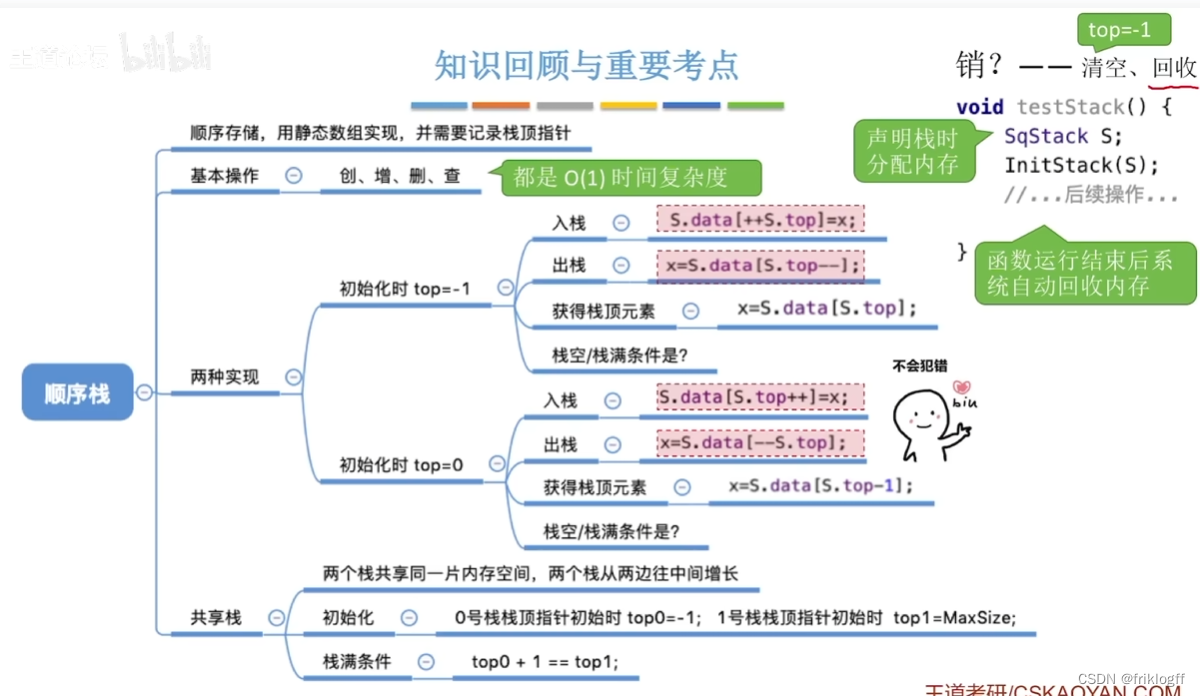
利用一组地址连续的存储单元存放自栈底到栈顶的数据元素,同时设一个栈顶指针(Top)
-
基础结构
-
栈顶指针,初始值:S.top = -1(若有元素,则指向栈顶元素S.data[S.top])

-
进栈:栈不满时,栈指针先+1,再送值到栈顶
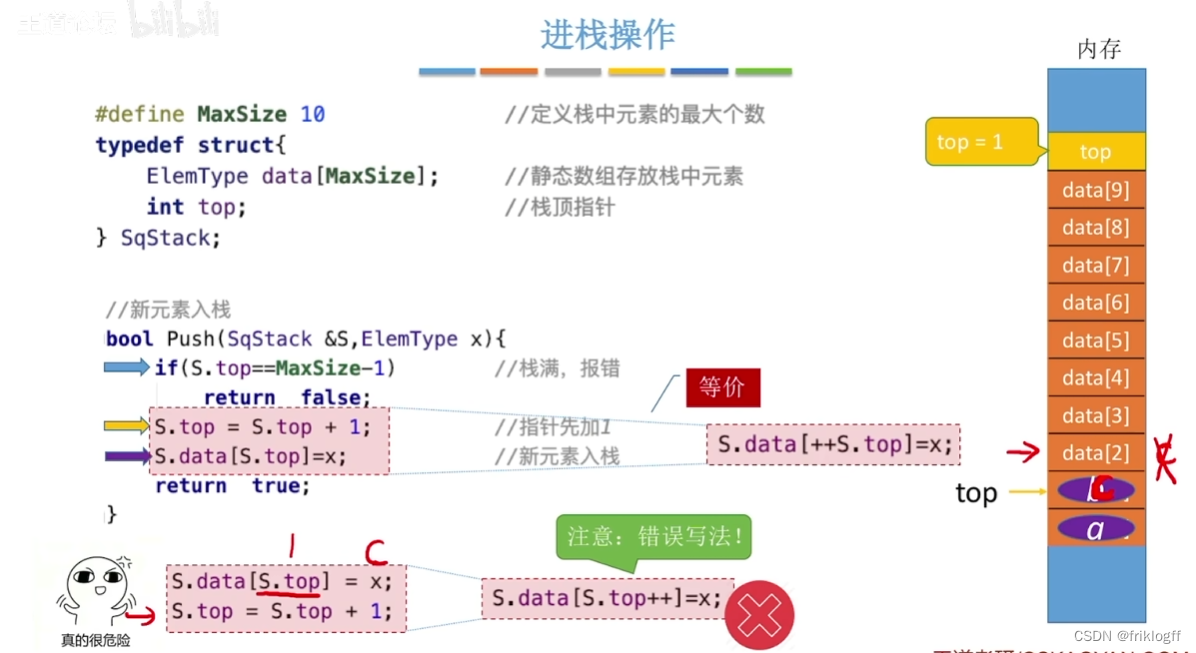
- 出栈:栈非空时,先取栈顶元素值,再将栈顶指针-1
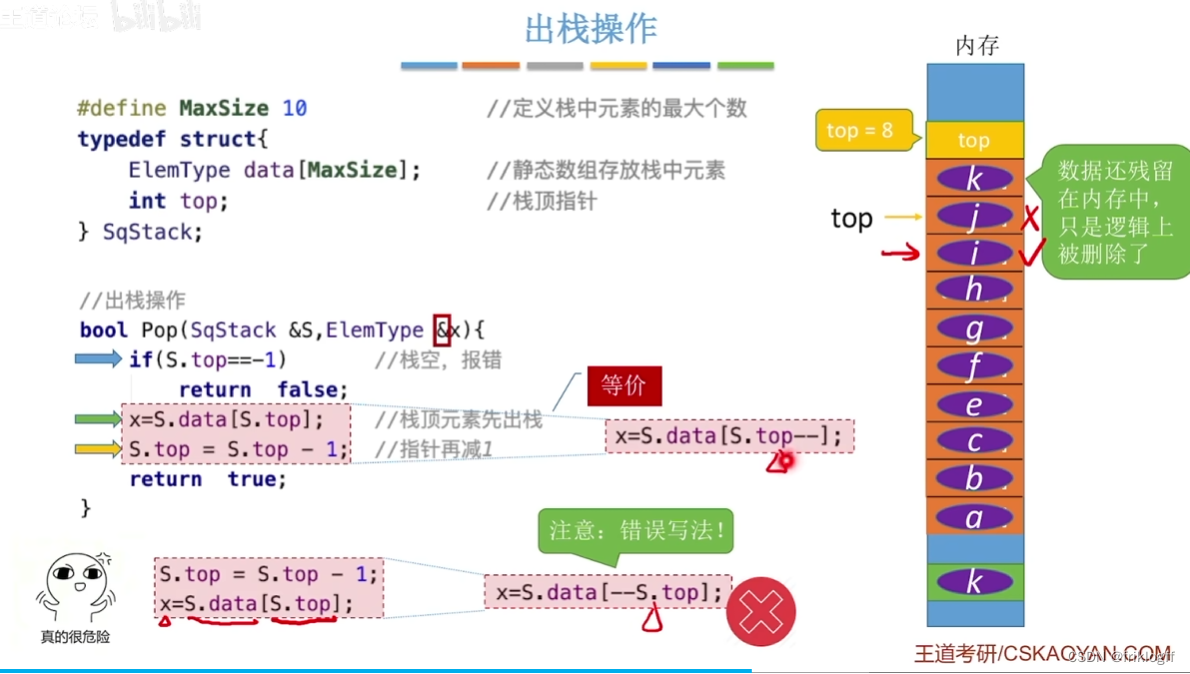
- 出栈:栈非空时,先取栈顶元素值,再将栈顶指针-1
-
栈空条件:S.top == -1
-
栈满条件:S.top == MaxSize-1
- 栈长:S.top + 1
-
-
-
-
-
顺序栈的基本操作
- 初始化、判栈空、进栈、出栈、读栈顶元素(本质就是操作顺序表)

- 初始化、判栈空、进栈、出栈、读栈顶元素(本质就是操作顺序表)
-
S.top == 0

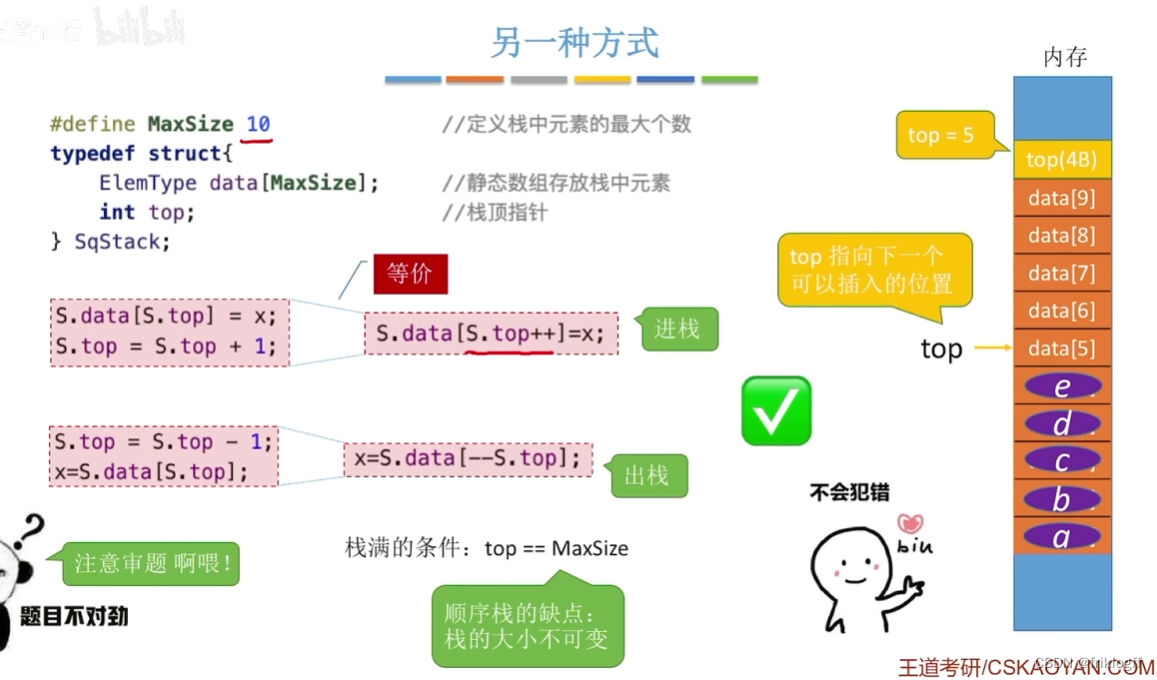
共享栈
- 共享栈
-

-
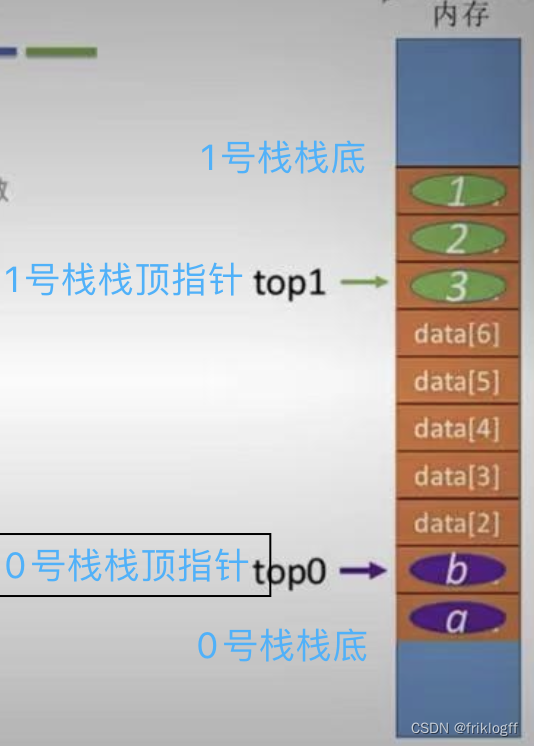
概念
- 让两个顺序栈共享一个一维数组空间,将两个栈的栈底分别设置在共享空间的两端,两个栈顶向共享空间的中间延伸
-
原则
-
栈空判断:top0 = -1时0号栈为空,top1 = MaxSize时1号栈为空
-
栈满判断:两个栈顶指针相邻(即top1-top0 == 1)时
-
其他操作和顺序栈类似
-
-
链栈

-
栈的链式存储结构
-

-
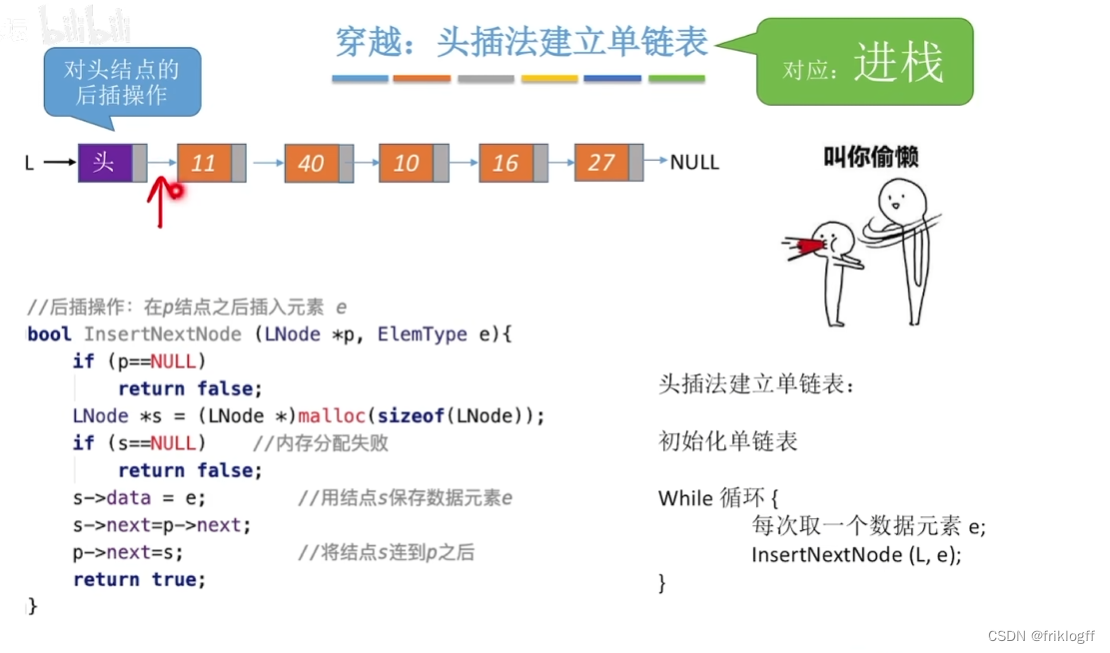
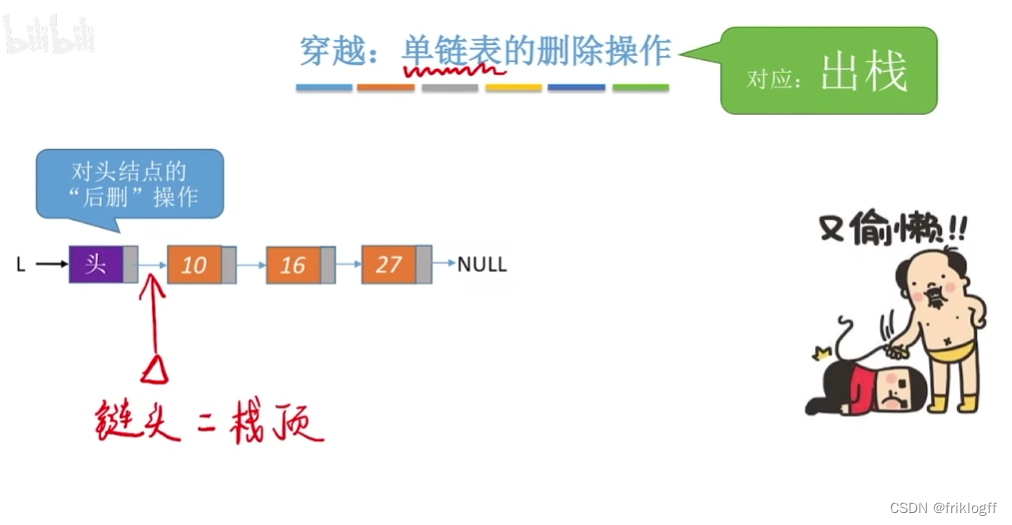
采用单链表实现,并规定所有操作都是在单链表的表头进行

-
优点
- 便于多个栈共享存储空间和提高效率,不存在栈满上溢的情况
队列
队列的概念
-


-
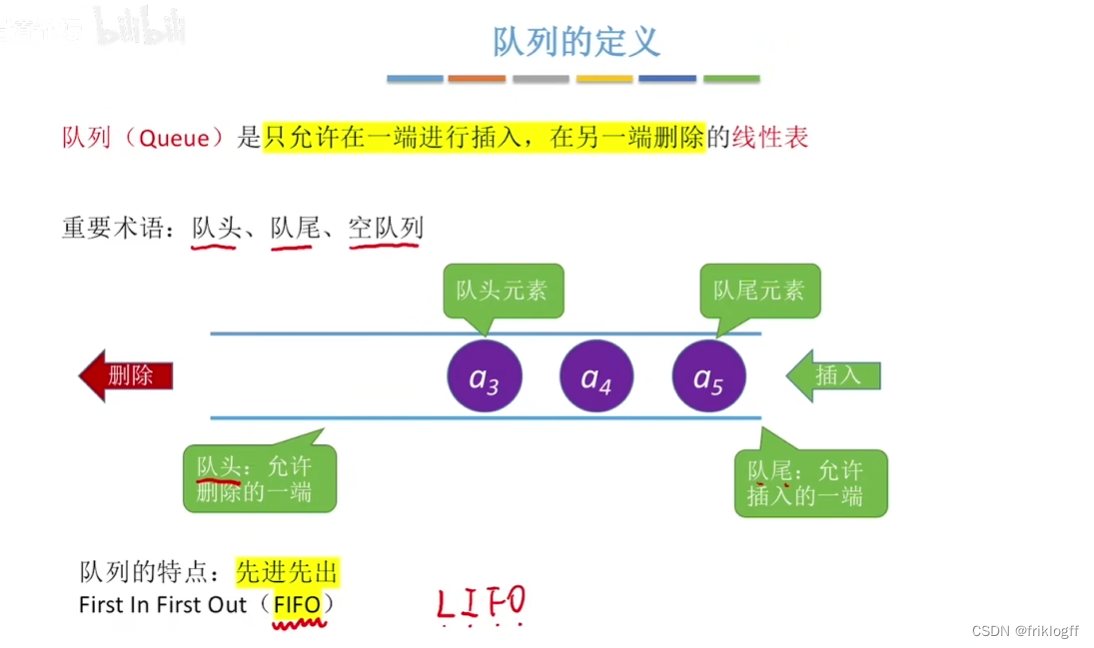
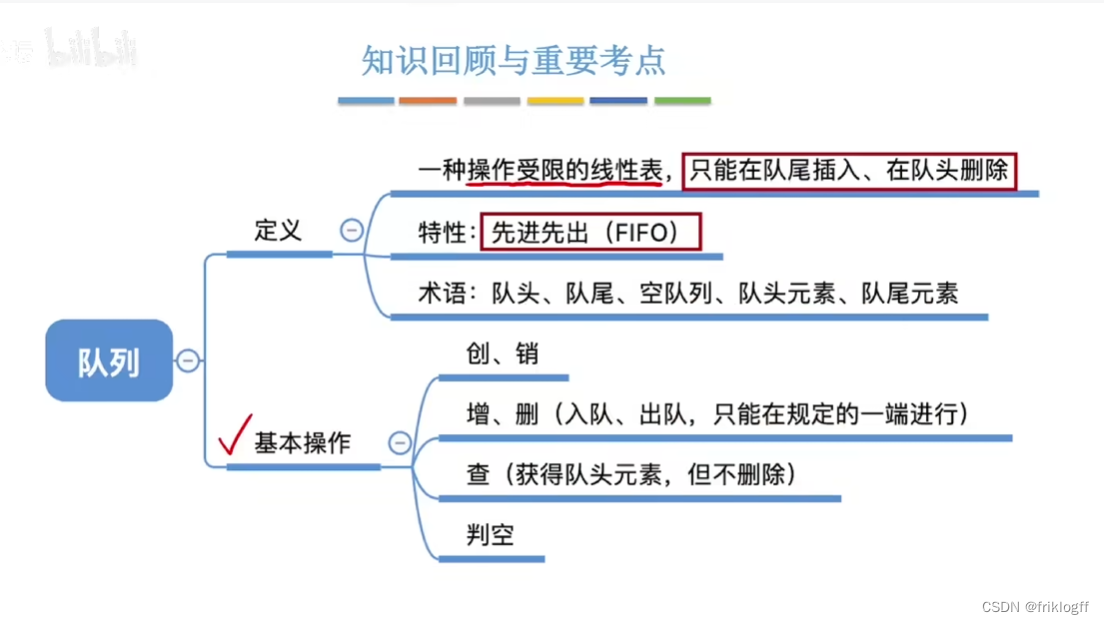
是一种操作受限的线性表,只允许在表的一端进行插入(队尾),另一端进行删除(队头)
- 特殊的线性表,先进先出(FIFO)
-
队头:删除元素的一端
- 队尾:插入元素的一端
- 队尾:插入元素的一端
-
队列的实现
队列的顺序存储结构
- 队列的顺序存储结构
-

-
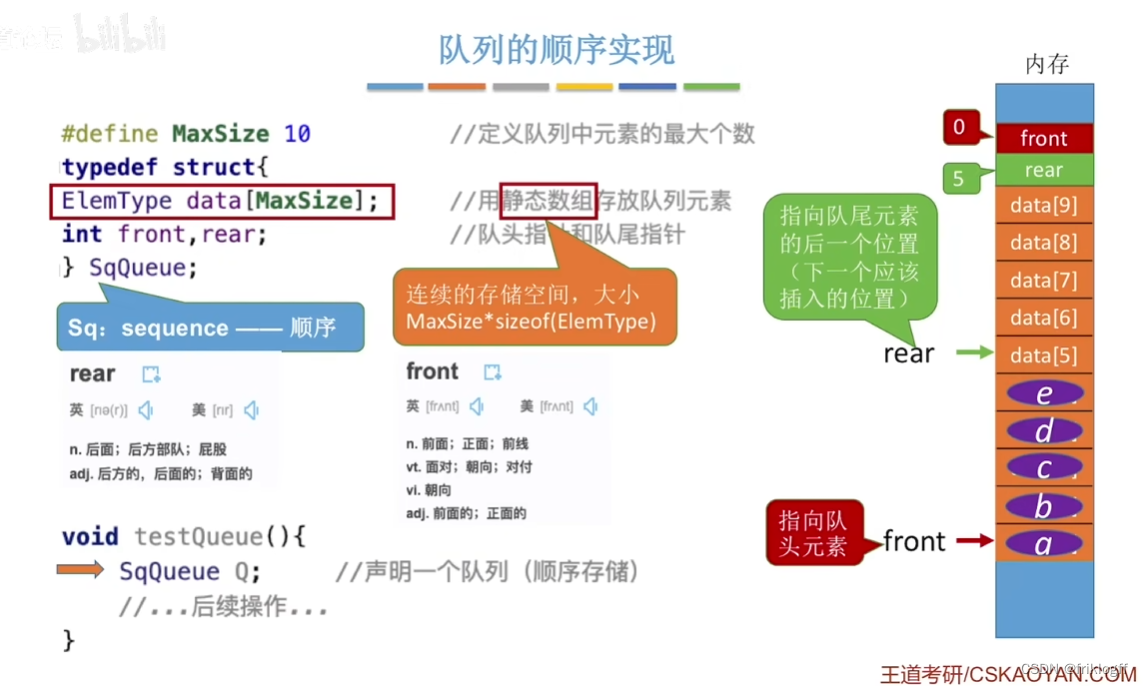
分配一块连续的存储单元存放队列元素,设两个指针
- 队头指针front:指向队头元素
队尾指针rear:指向队尾元素的下一个元素
- 队头指针front:指向队头元素
-
基础结构
-
初始状态(队空条件):Q.front == Q.rear == 0

-
进队操作:队不满时,先送值到队尾元素,再将队尾指针+1
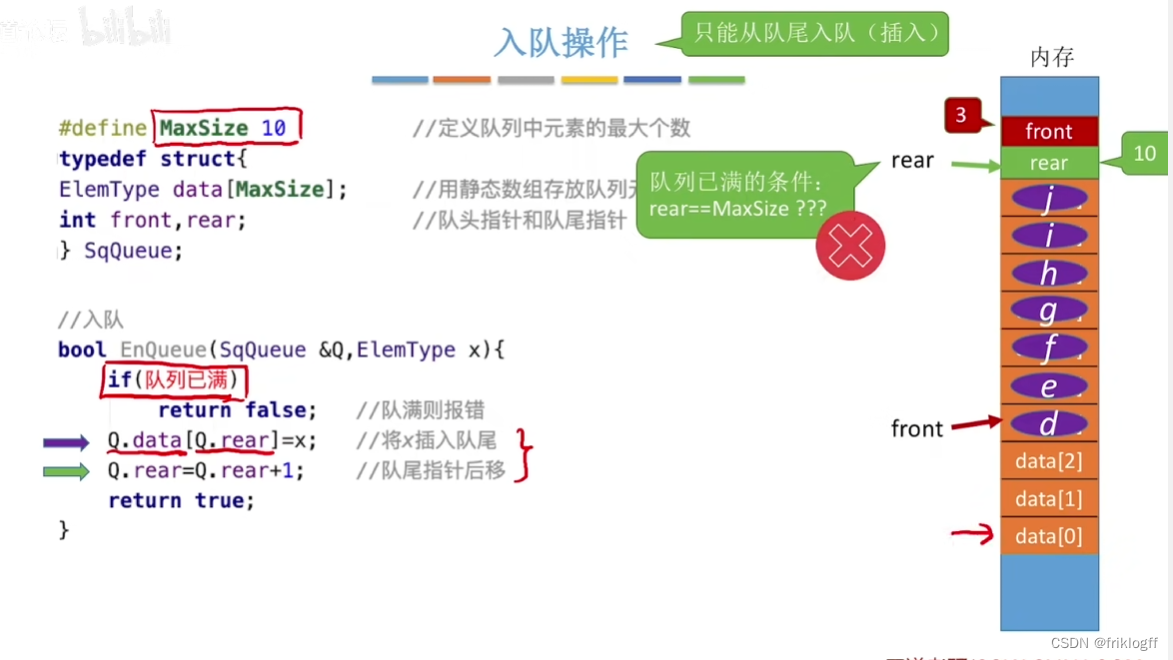
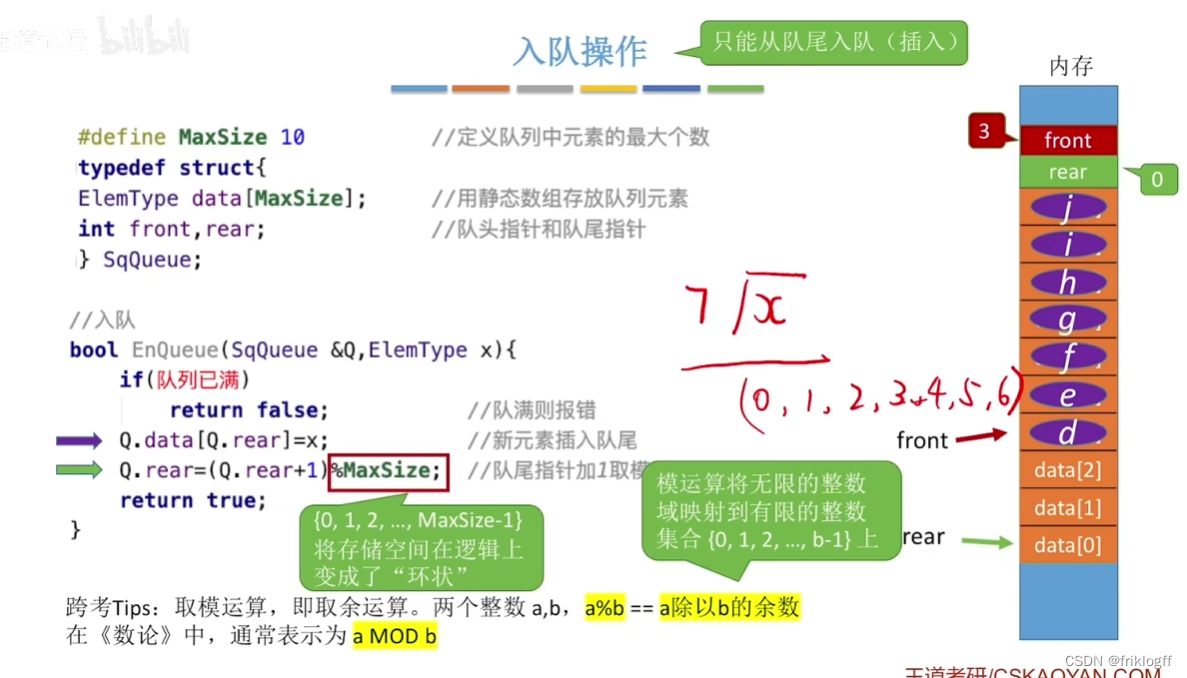
-
出队操作:队不空时,先取队头元素值,再将队头指针+1
-
-
假溢出:在data数组依然存在空位置时,却已经满足队列满的条件(出栈的元素位置空闲)
-
-
循环队列(解决假溢出问题)
-
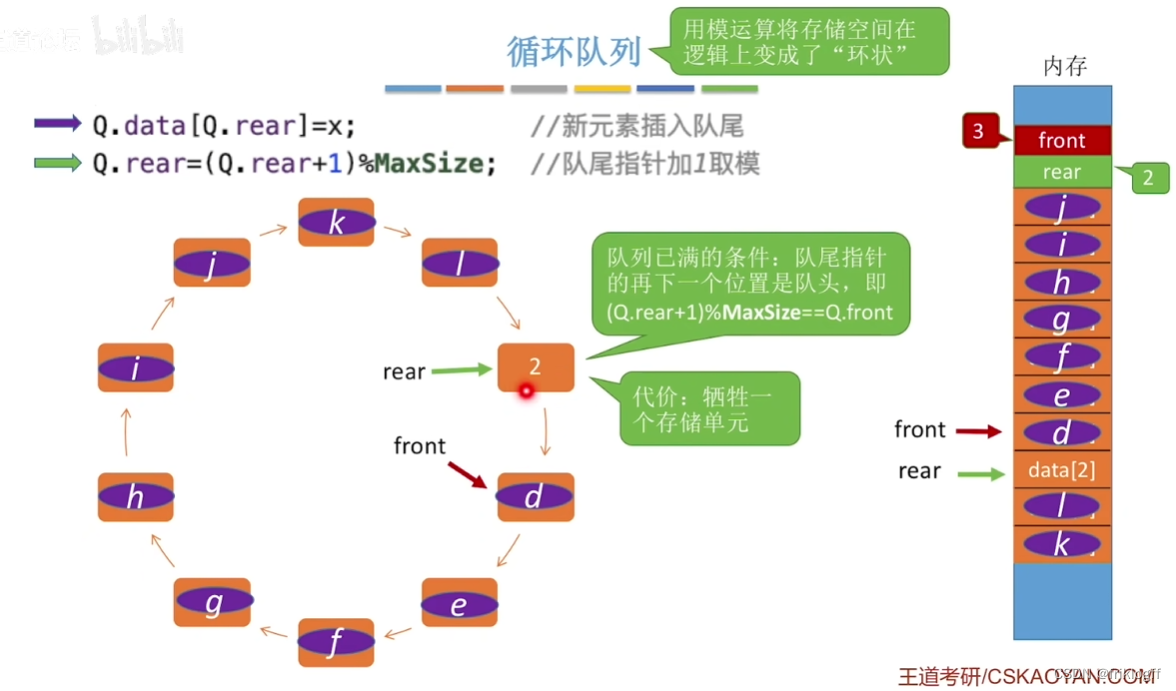
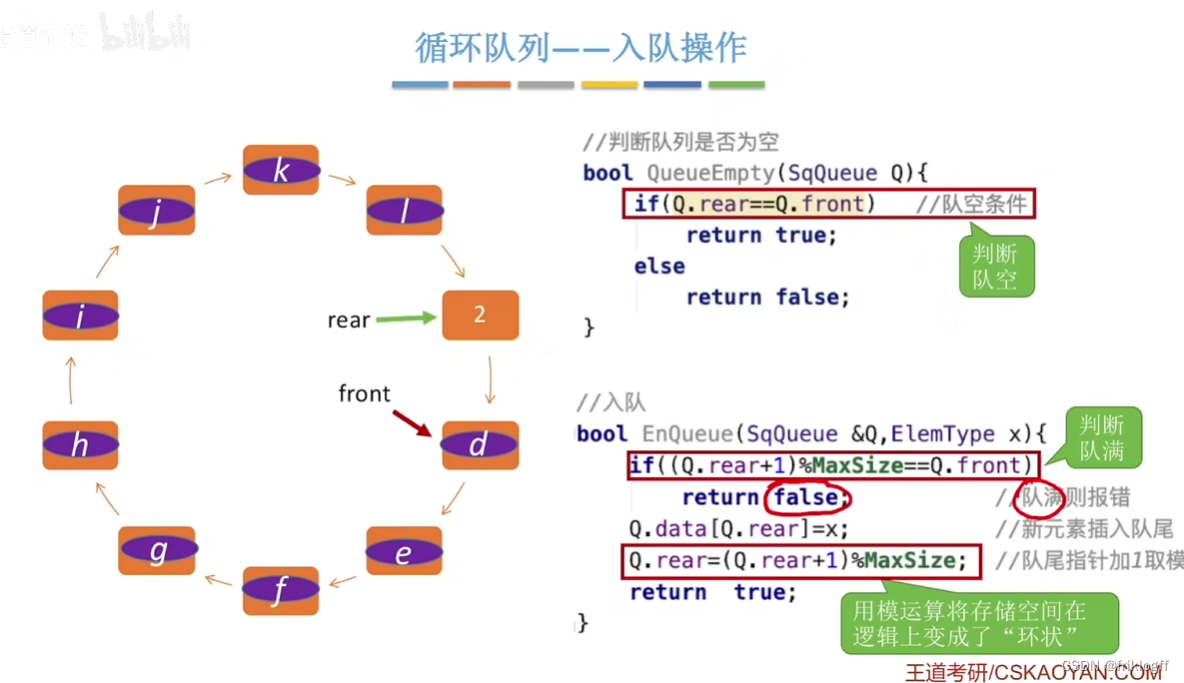
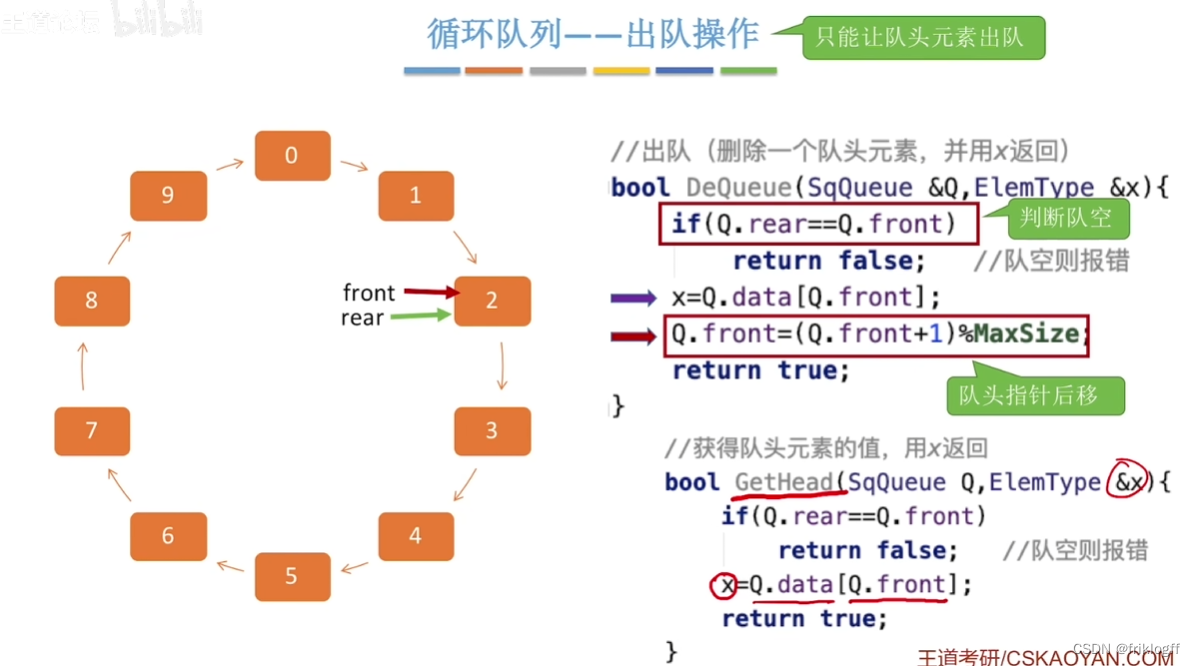
-
概念
- 把存储队列元素的表逻辑上视为一个环
-
基本操作
-
初始时:Q.front = Q.rear = 0
-
队头指针+1:Q.front = (Q.front + 1) % MaxSize
-
队尾指针+1:Q.rear = (Q.rear + 1) % MaxSize
-
队列长度:(Q.rear + MaxSize - Q.front) % MaxSize
-
队空:Q.front == Q.rear
-
-
队满判断
-
牺牲一个单元来区分队空和队满,即队头指针在队尾指针的下一位置作为队满标志
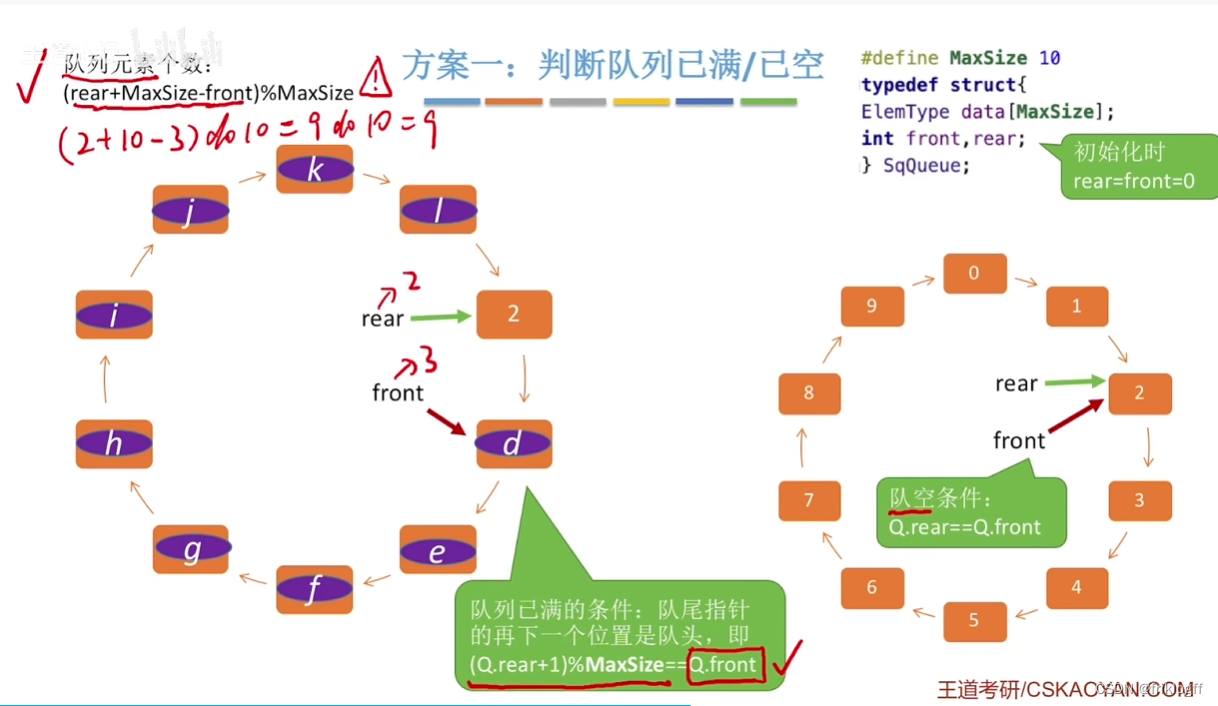
- 队满条件:(Q.rear + 1) % MaxSize == Q.front
-
类型中增设表示元素个数的数据成员(int size)

-
队空:Q.size == 0
-
队满:Q.size == MaxSize
-
-
类型中增设tag数据成员,以区分是队满还是队空
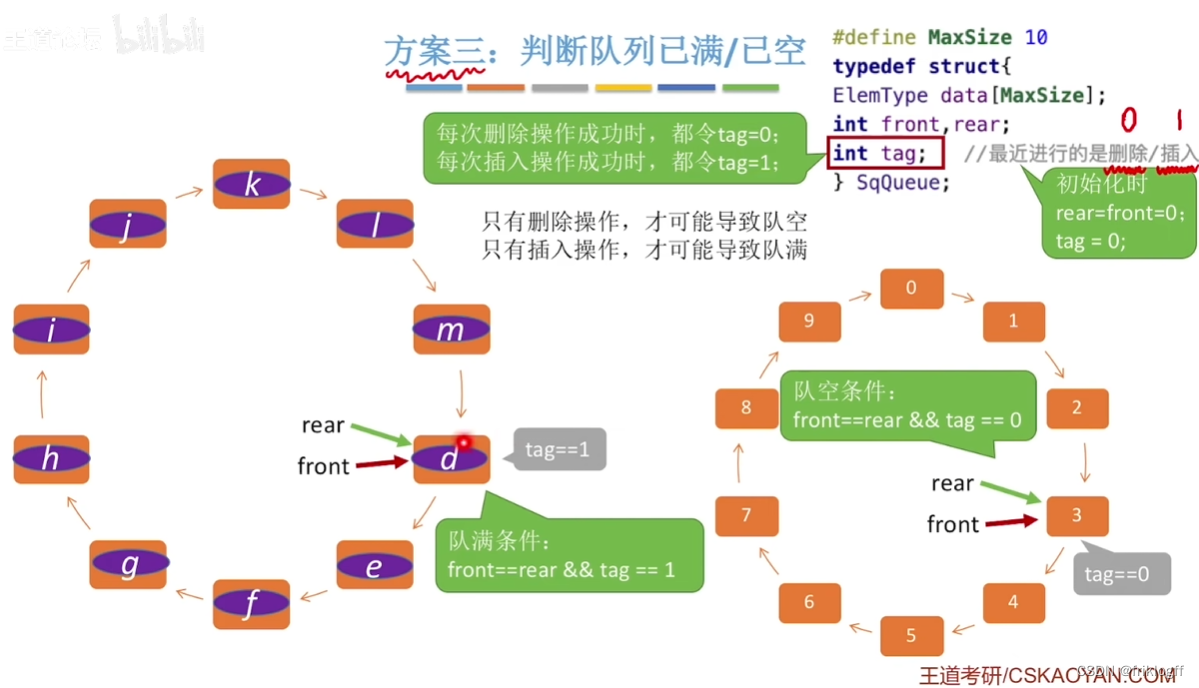
-
tag == 0时,若因删除导致Q.front == Q.rear,则队空
-
tag == 1时,若因插入导致Q.front == Q.rear,则队满
-
-
-
-
-
rear指向队尾元素
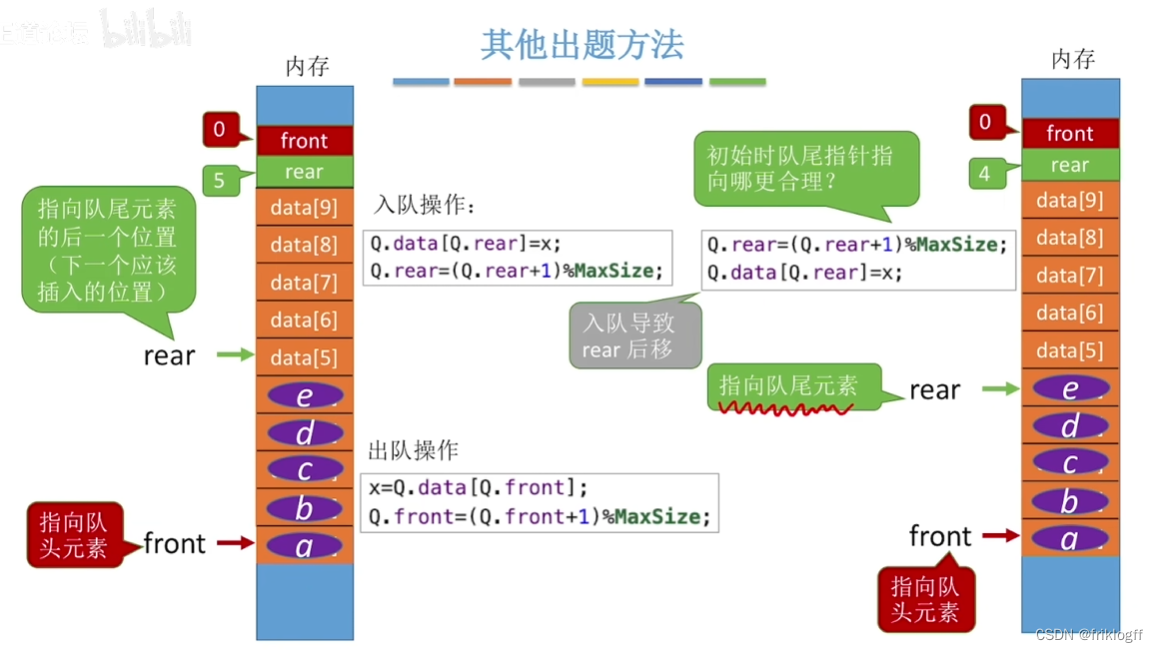
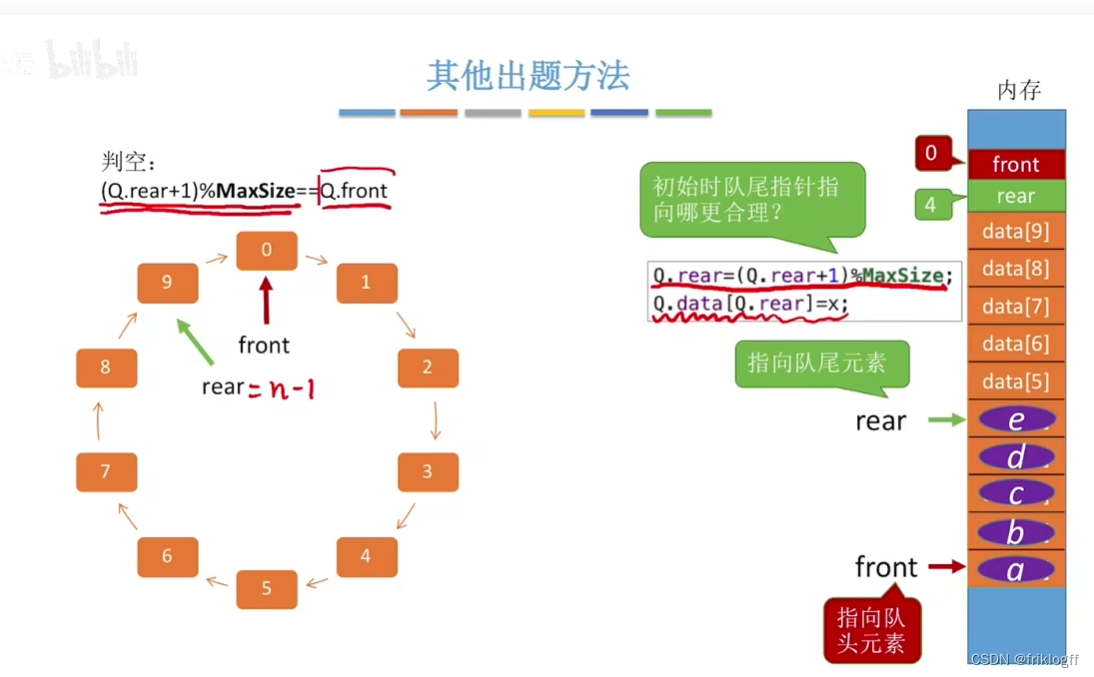
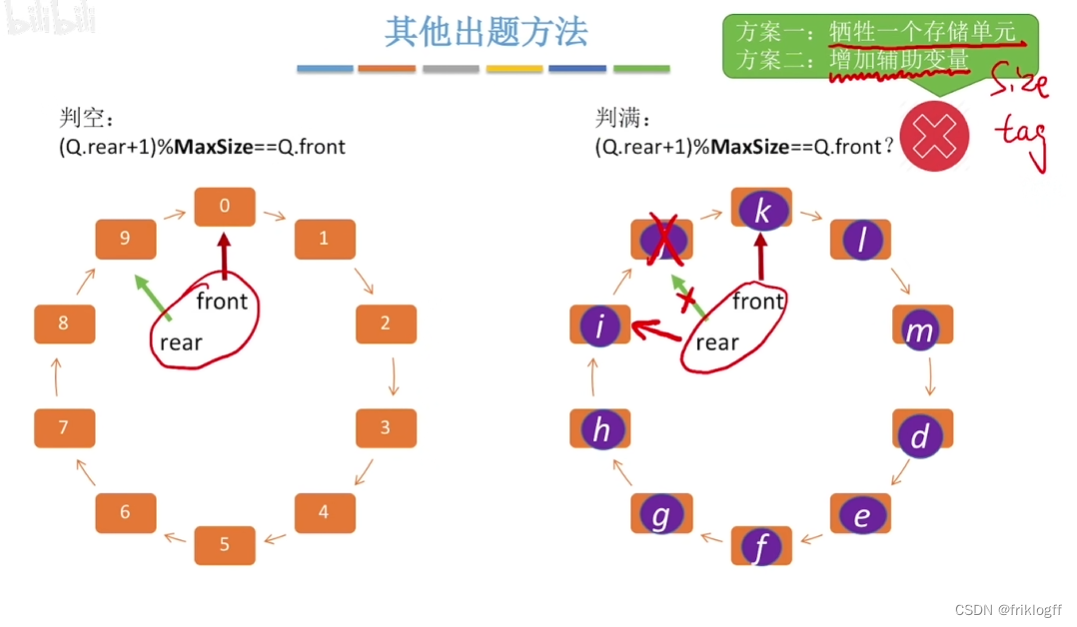
牺牲一个存储单元
- front在rear后两个位置,队满
- front在rear后一个位置,队满
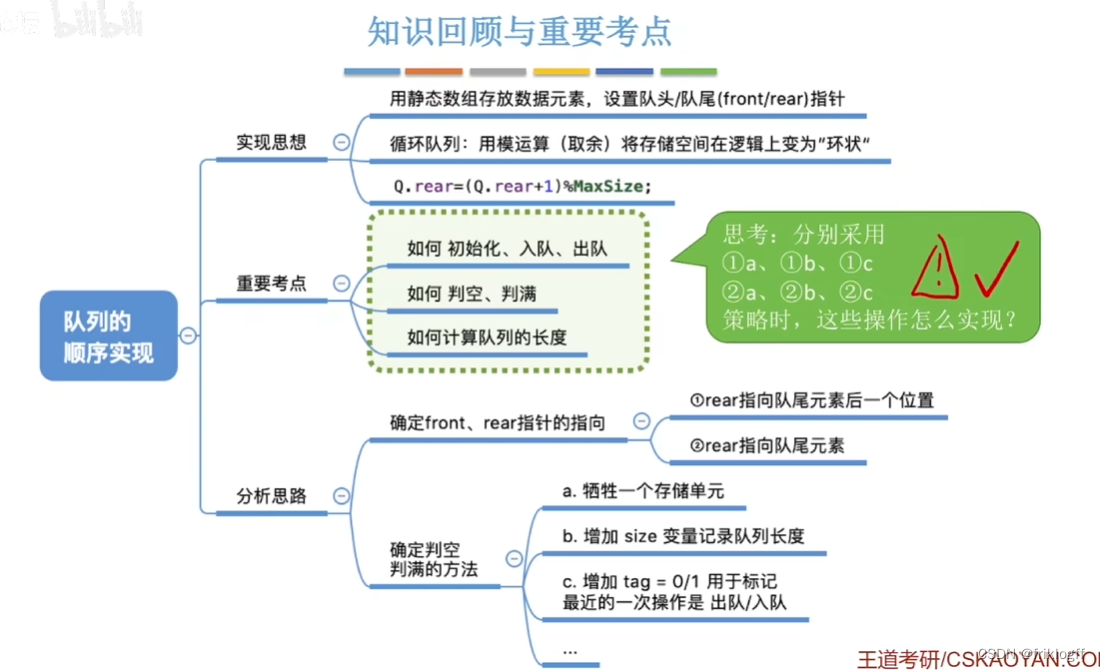
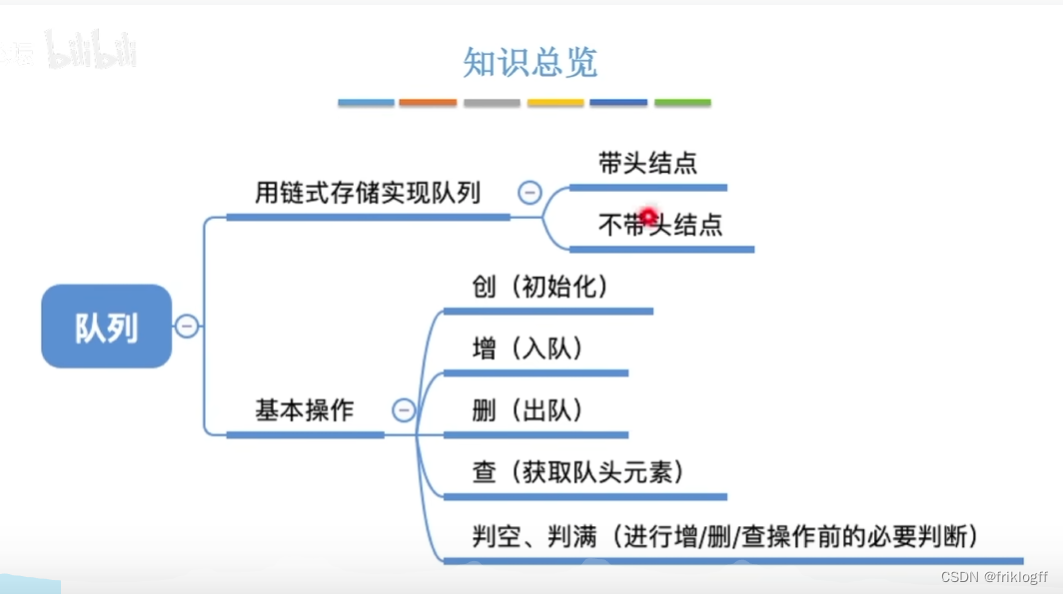
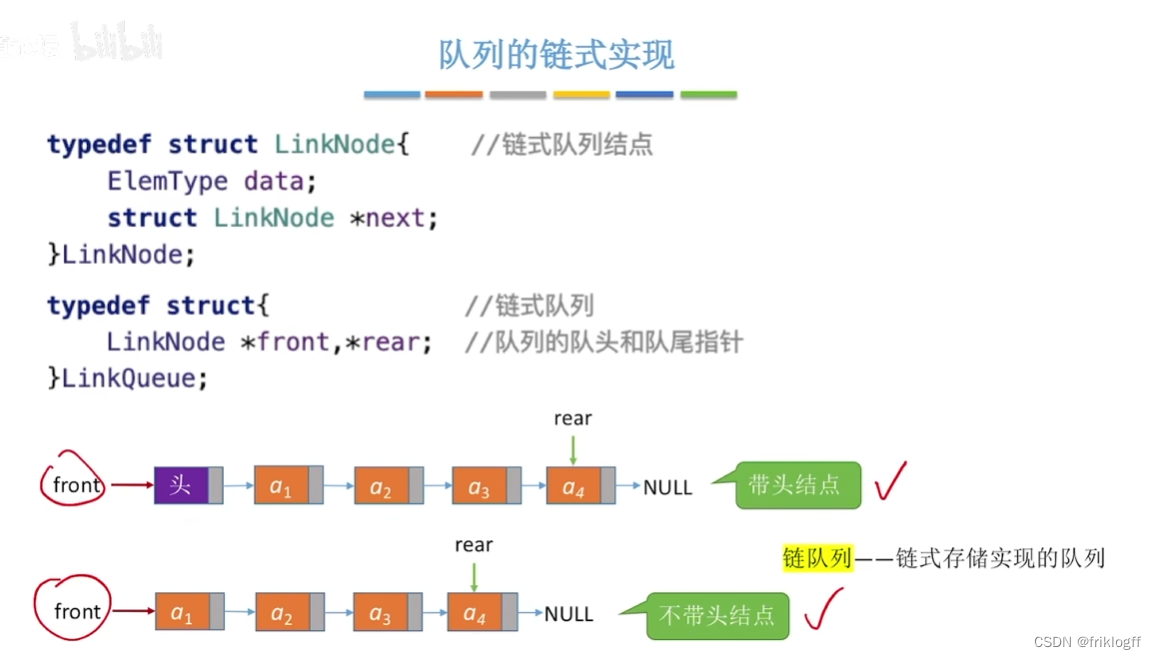
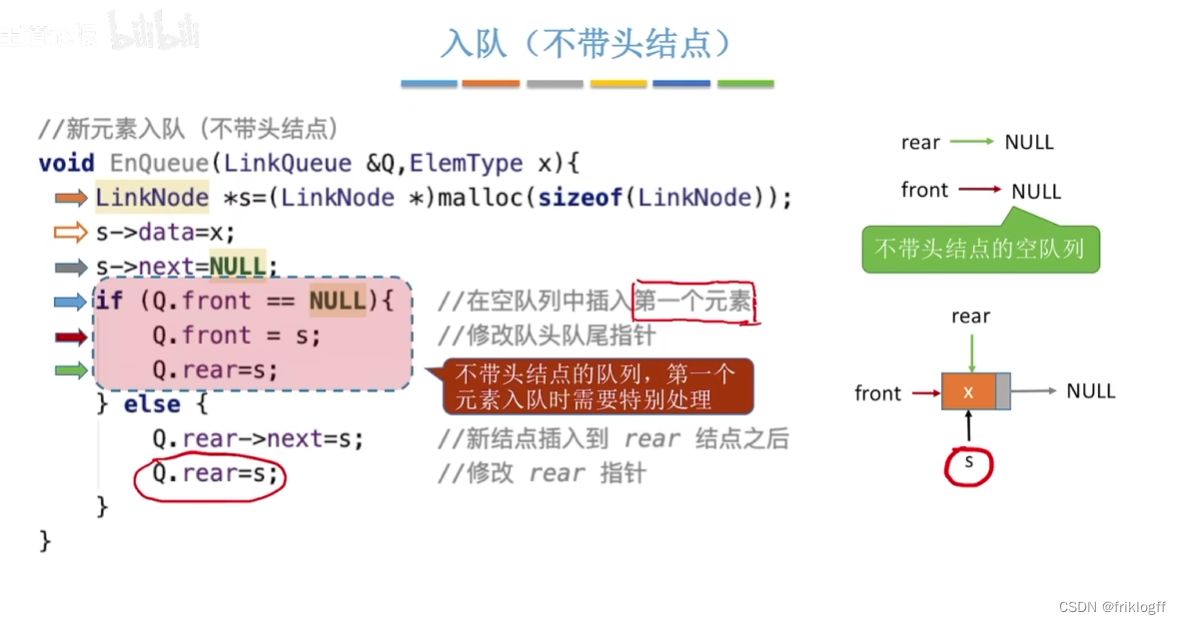
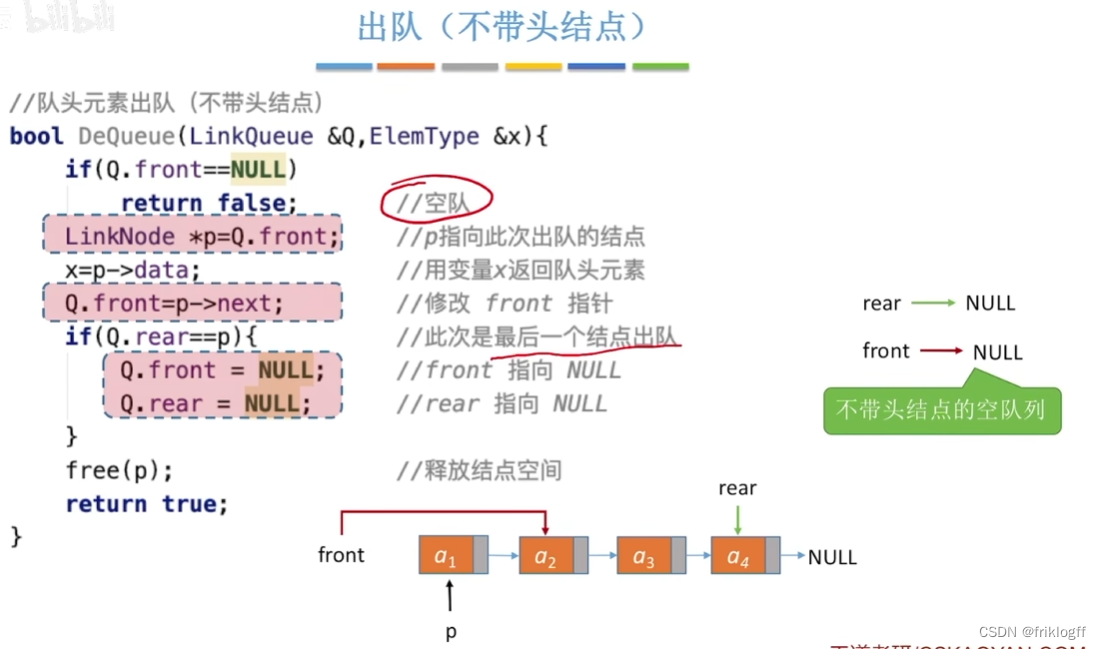
队列的链式存储结构
- 队列的链式存储结构
-
-
队列的链式表示时一个同时带有队头指针和队尾指针的单链表
-
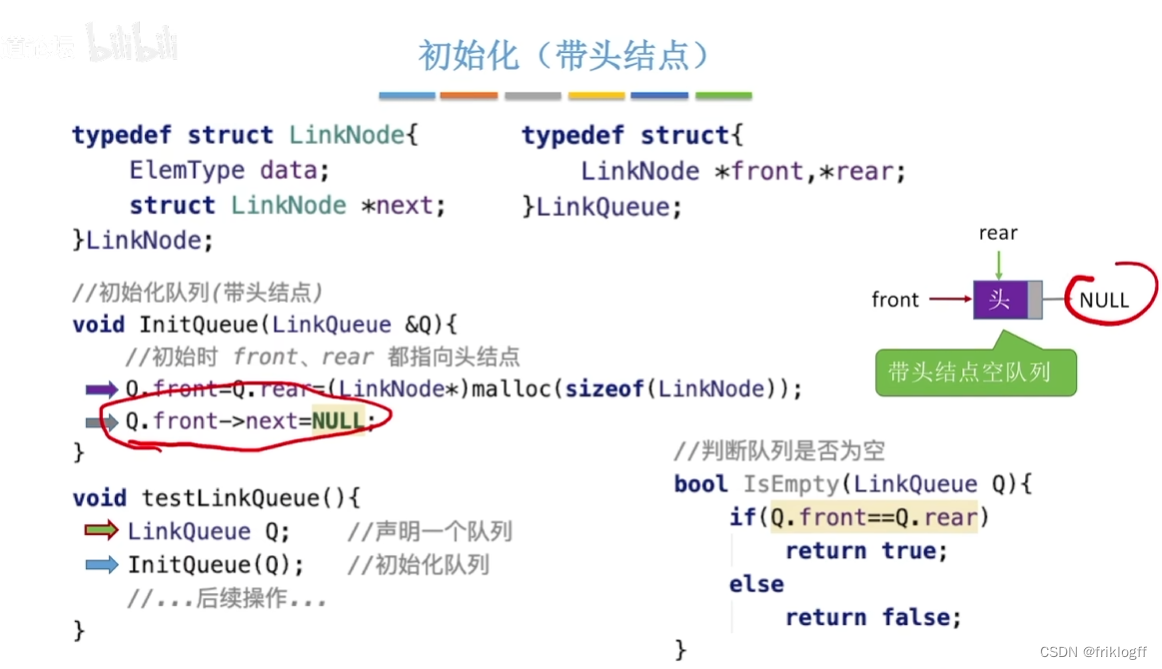
头指针指向队头结点,队尾指针指向队尾结点,当Q.front == NULL且Q.rear == NULL时,队列为空

-
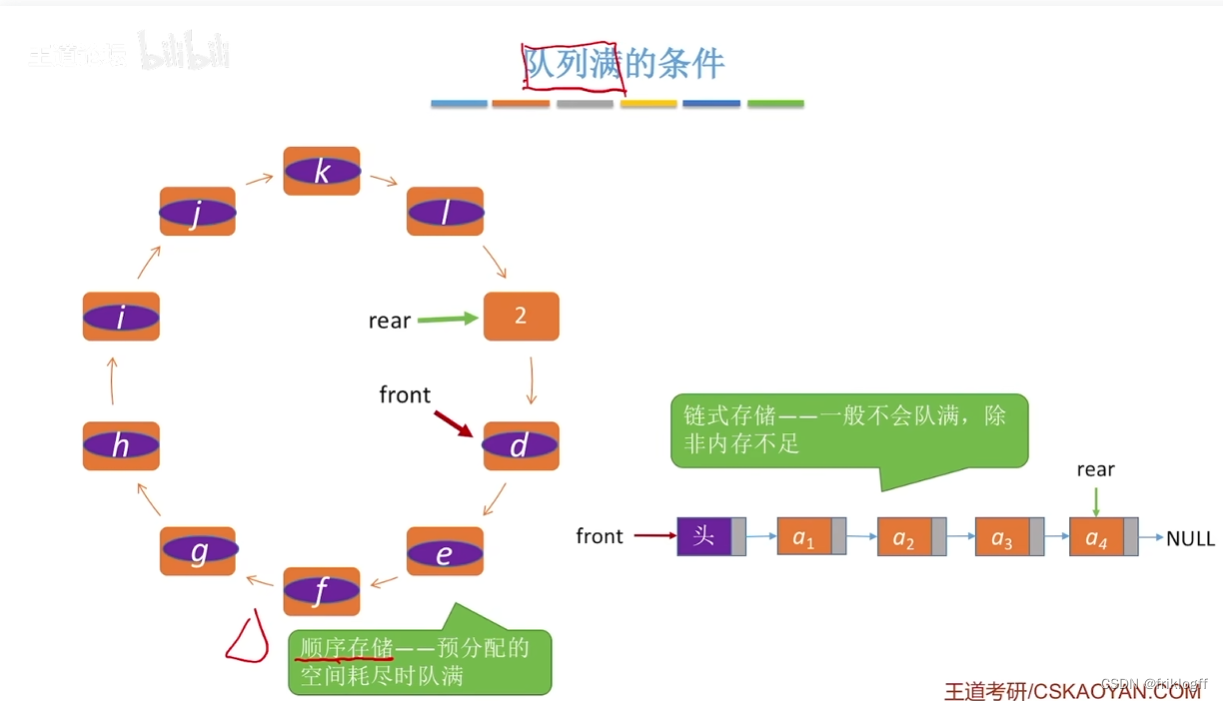
不存在队列满且溢出问题,适合于数据元素变动较大的情况
-
-
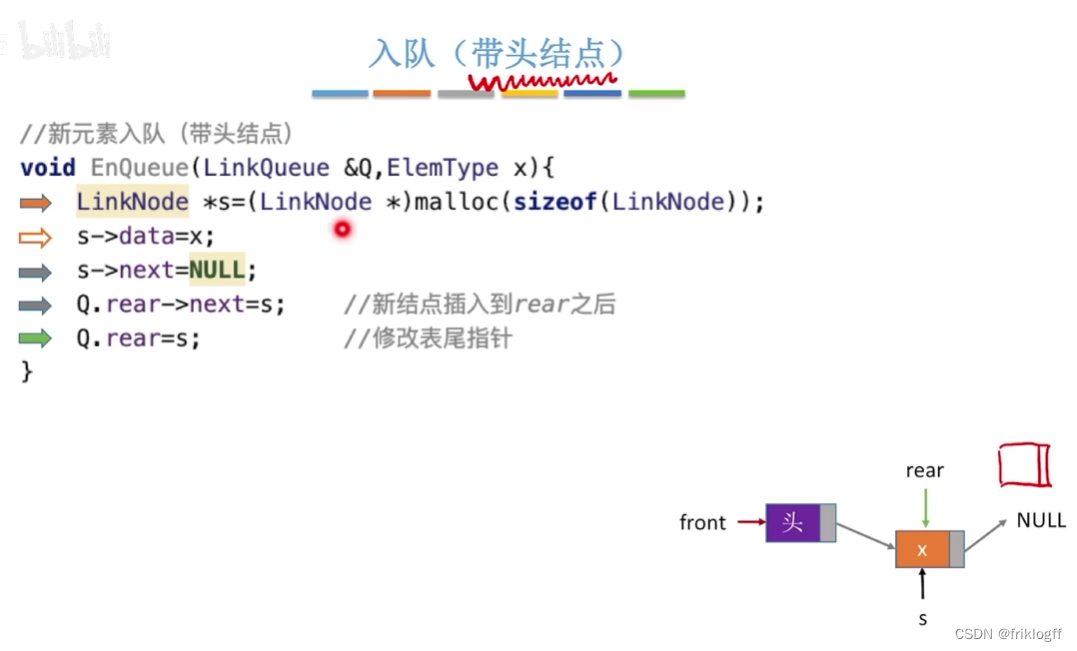

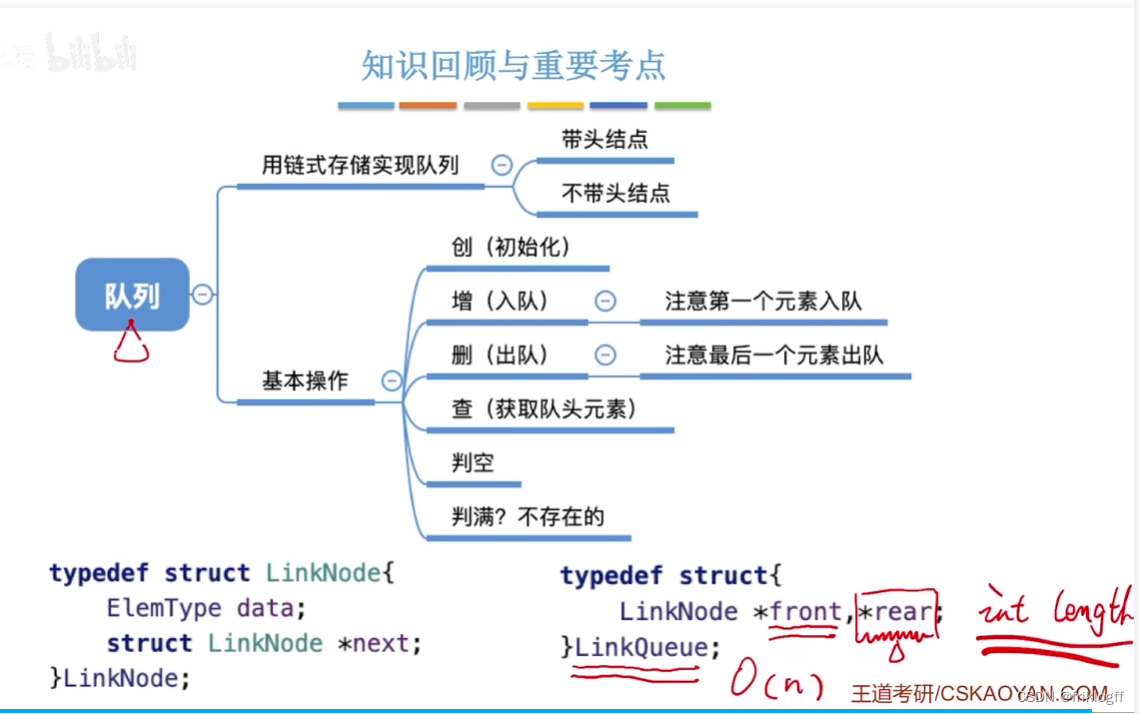
小结
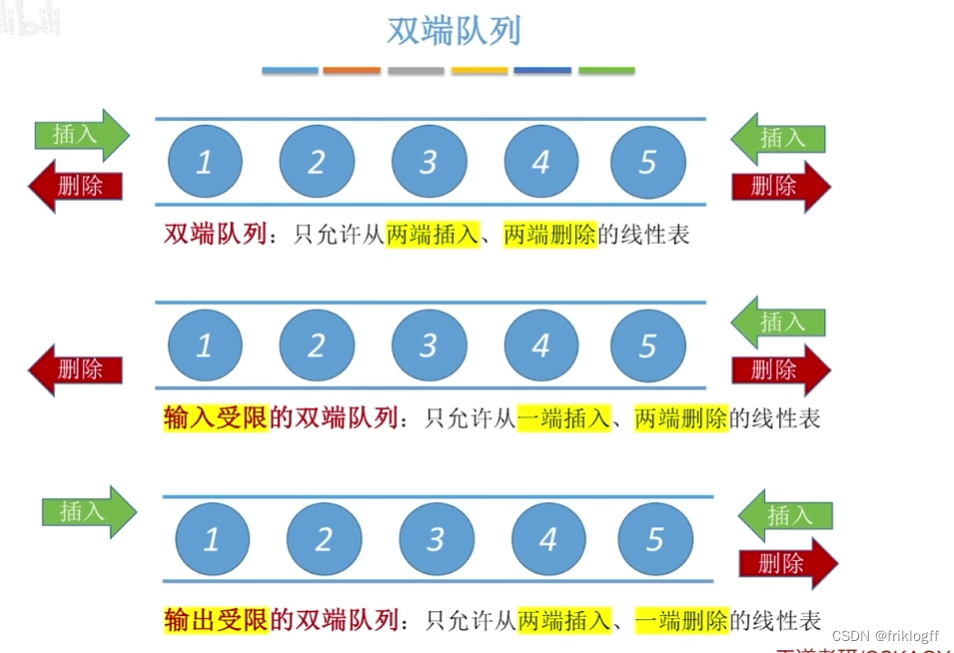
双端队列(挺喜欢考的考点)
-
概念
- 双端队列是指允许两端都可以进行入队和出队操作的队列,其逻辑结构仍是线性表

- 双端队列是指允许两端都可以进行入队和出队操作的队列,其逻辑结构仍是线性表
-
分类
-
输出受限的双端队列:允许在一端进行插入和删除,但在另一端只允许插入的双端队列
-
输入受限的双端队列:允许在一端进行插入和删除,但在另一端只允许删除的双端队列
-
栈和队列有相同逻辑结构,线性结构

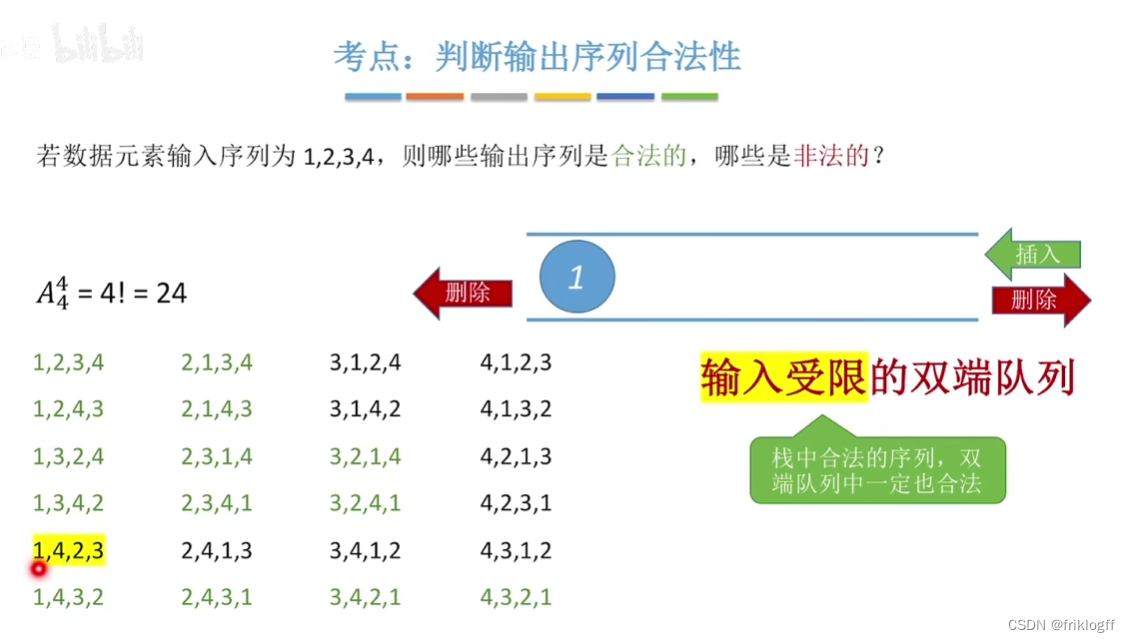
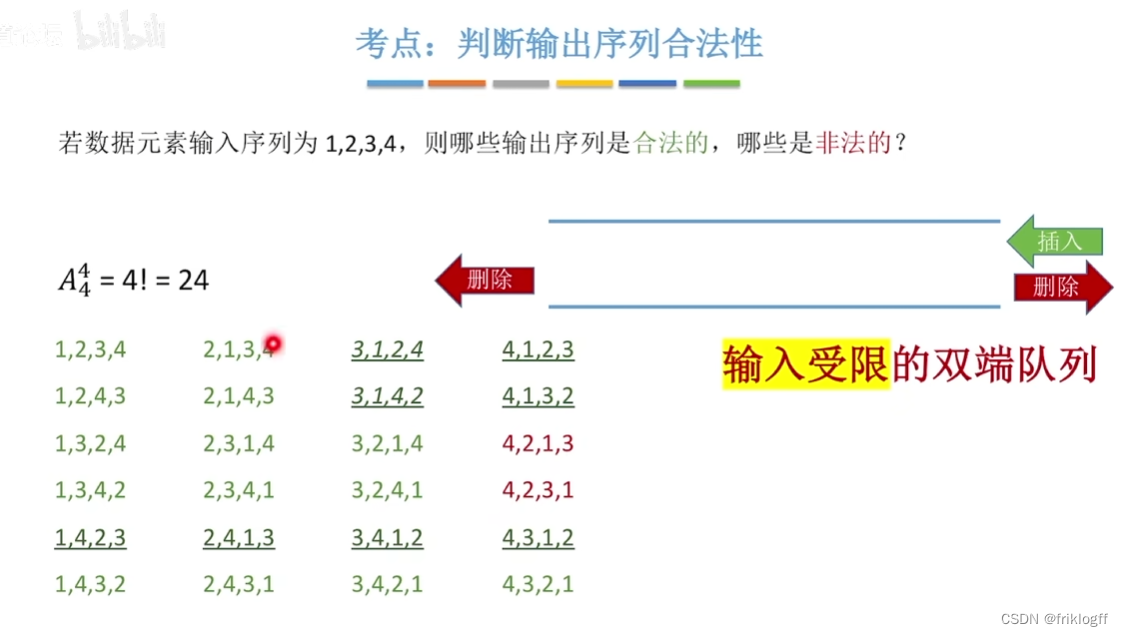
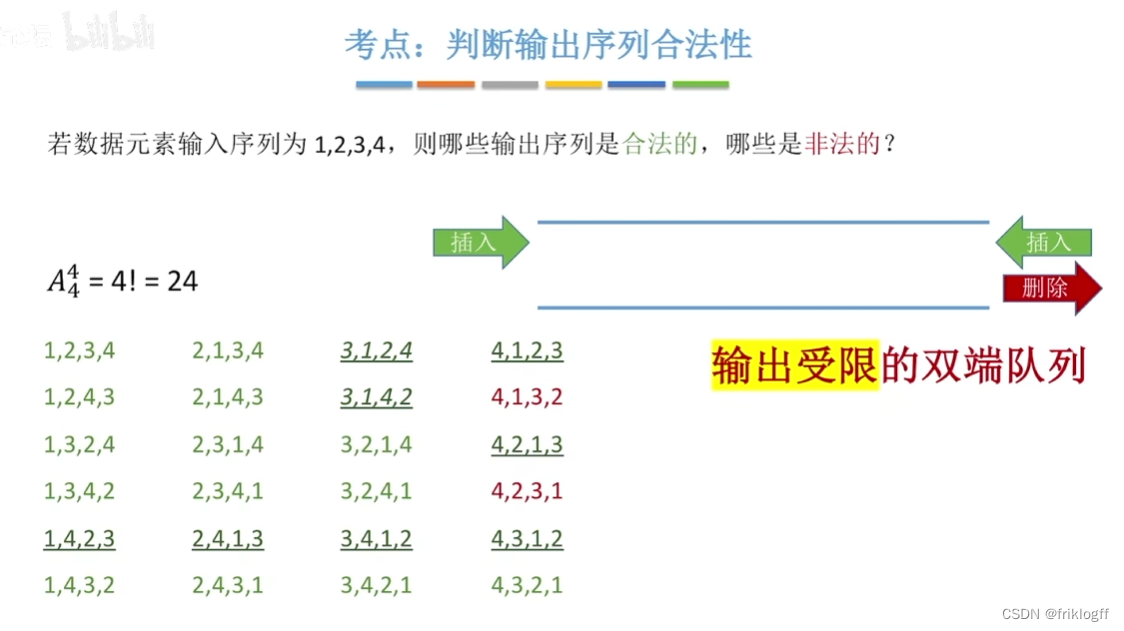
合适与不合适做链队的链表,关键看能不能获取到首尾指针(带首尾的非循环或带尾的循环)
- 单链表实现队列,队头只能设置在链头(关注删除操作,需找到新队头)
栈和队列的应用
栈的应用
括号
-
括号匹配
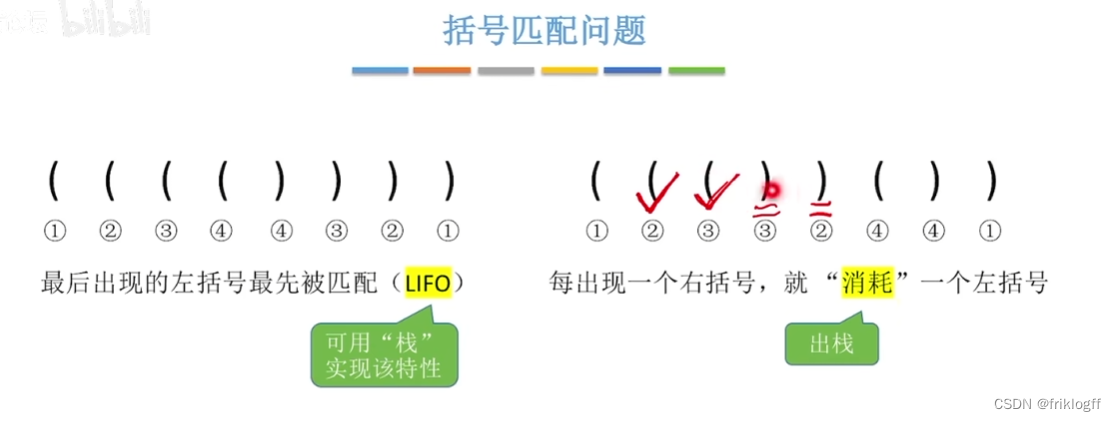
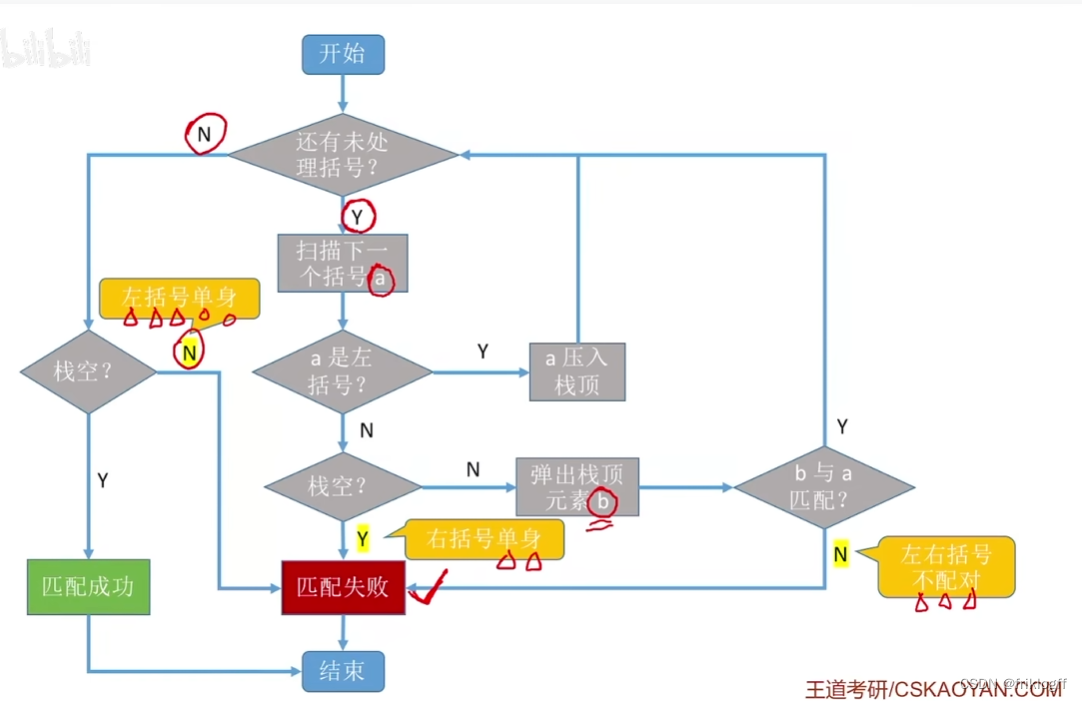

-
步骤
-
初始设置一个空栈,顺序读入括号
-
若右括号,则从栈中弹出一个符号,判断是否匹配
-
若左括号,则压入栈中
-
-
失败条件
- 不匹配、结束后栈仍有元素、遇右括号栈为空
-
表达式求值
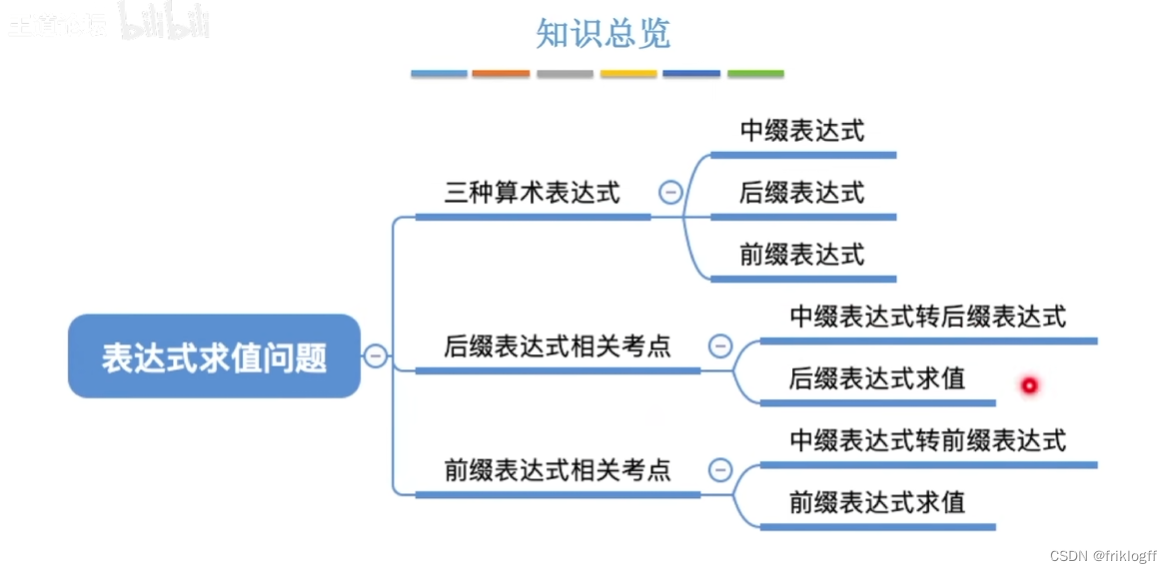
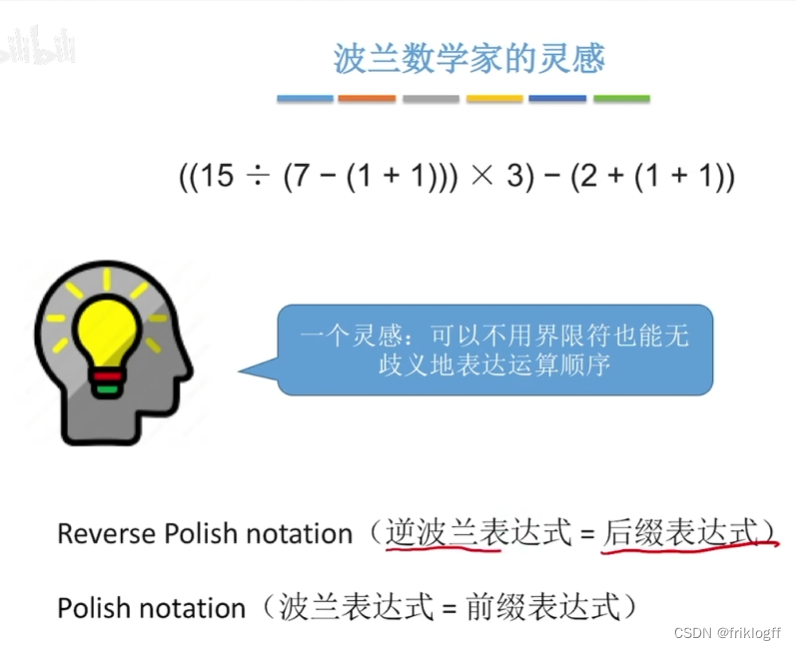
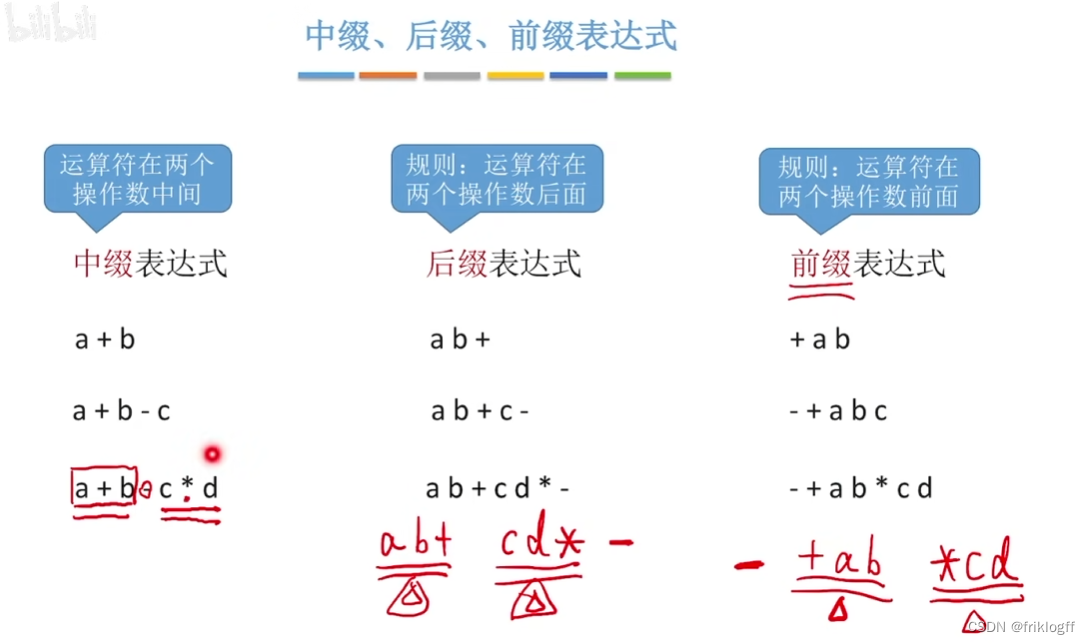
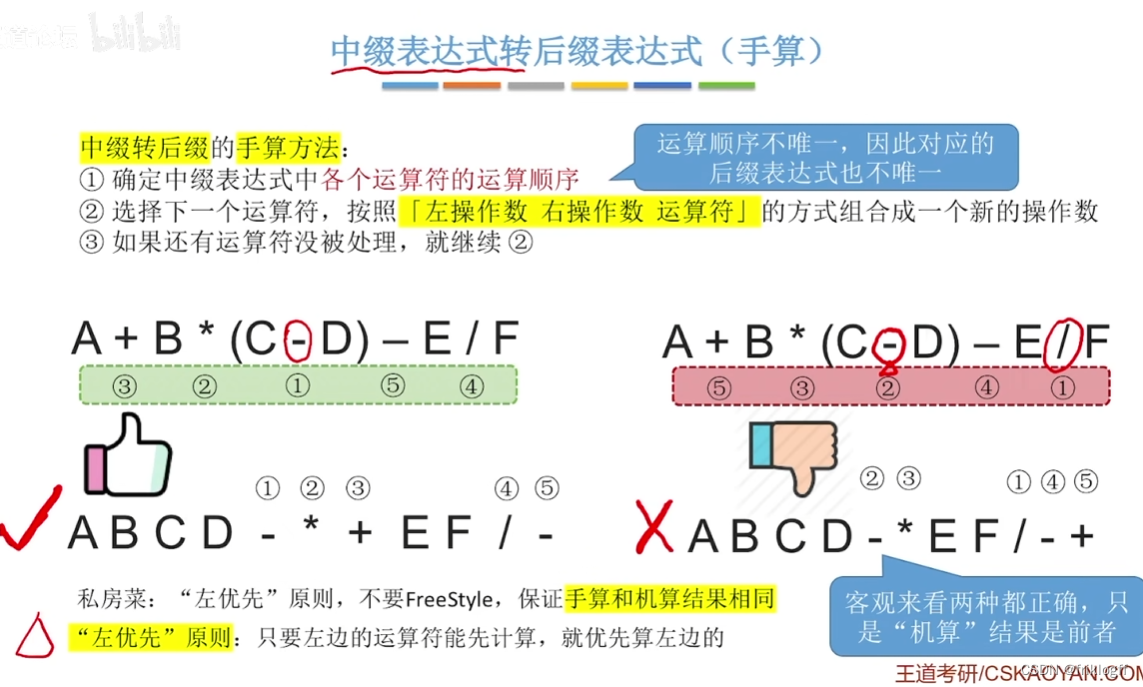
中缀表达式转后缀表达式
-
从左到右遍历各元素
-
若遇到操作数:直接加入后缀表达式
-
遇到界限符:“(”直接入栈;“)”则依次弹出栈内运算符并加入后缀表达式,直到弹出“(”为止
-
遇到运算符:依次弹出栈中优先级高于或等于当前运算符的所有运算符,并加入后缀表达式,若碰到“(”或栈空则停止,之后再把运算符入栈


-



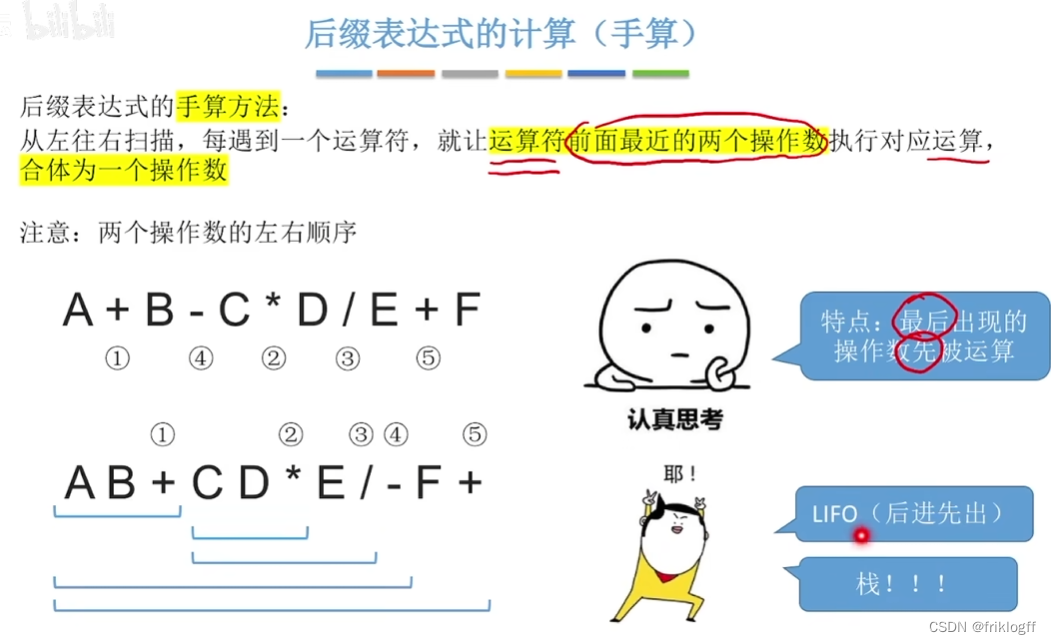
后缀表达式的计算
- 从左向右扫描元素,若扫描到操作数则压入栈,若扫描到运算符则弹出两个栈顶元素,执行运算将结构压回栈中


中缀表达式转前缀表达式
- 同理但从右到左遍历,“(”和“)”与中缀转后缀的功能相反,最后结果依次翻转


前缀表达式的计算
- 从右向左扫描元素,若扫描到操作数则压入栈,若扫描到运算符则弹出两个栈顶元素,执行运算将结构压回栈中

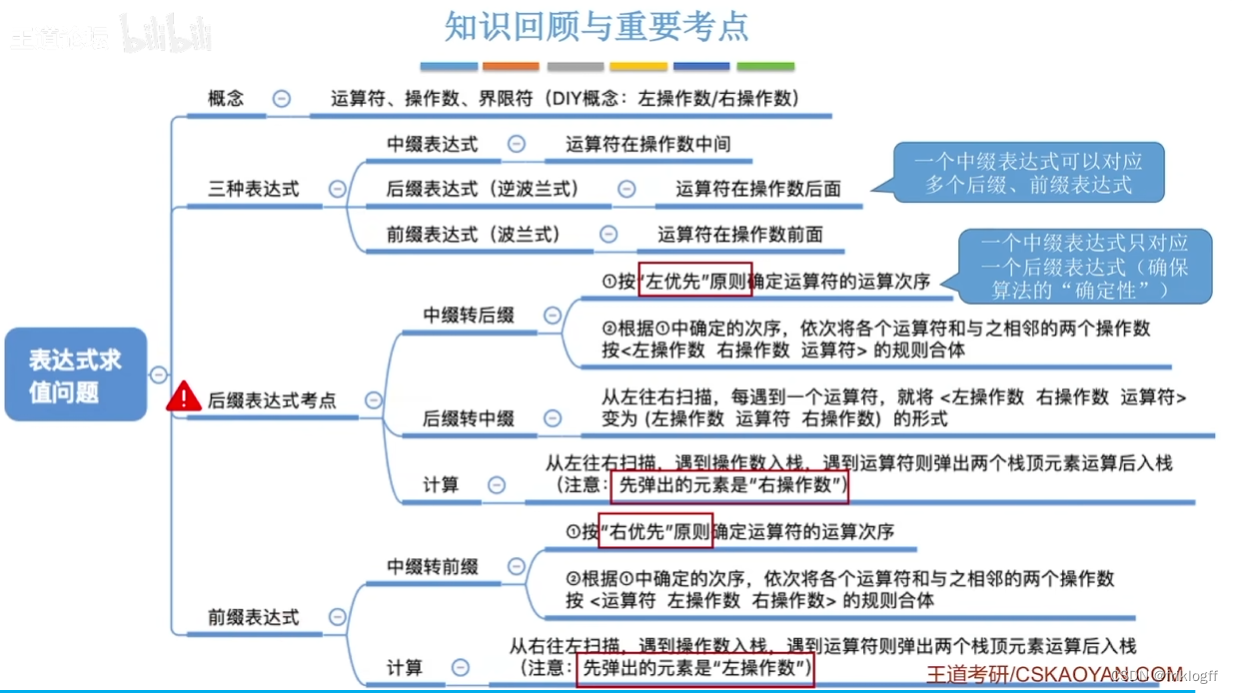
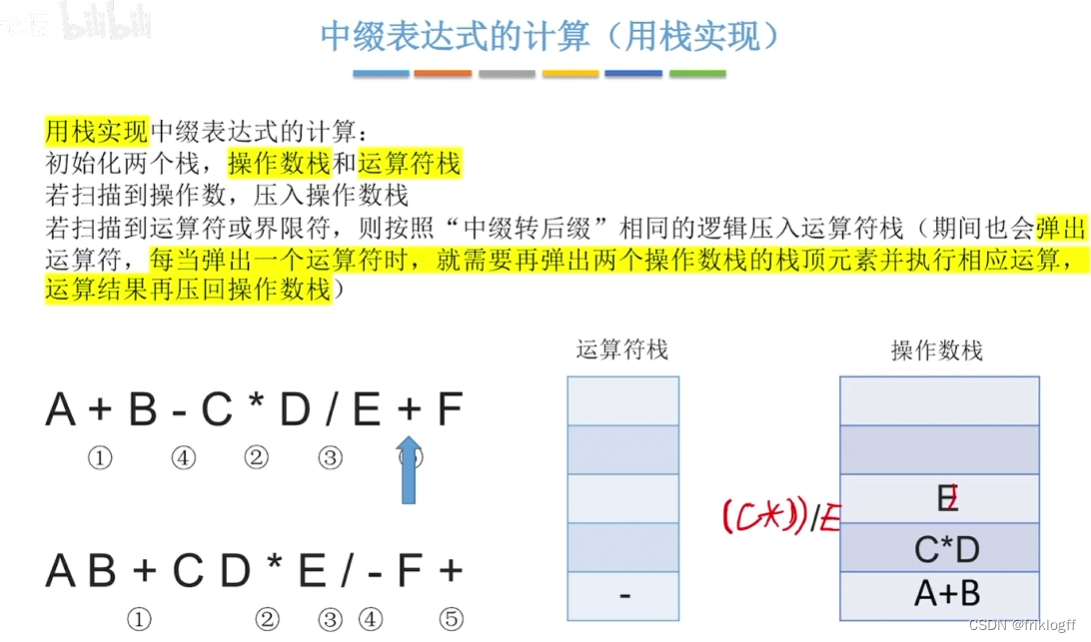
中缀表达式的计算(用栈实现)
-
初始化操作数栈和运算符栈
-
若扫描到操作数,压入操作数栈;若扫描到运算符或界限符,按“中缀转后缀”的逻辑压入运算符栈(可能弹出运算符,若弹出则将栈顶的两个操作数运算压回操作数栈)




其他
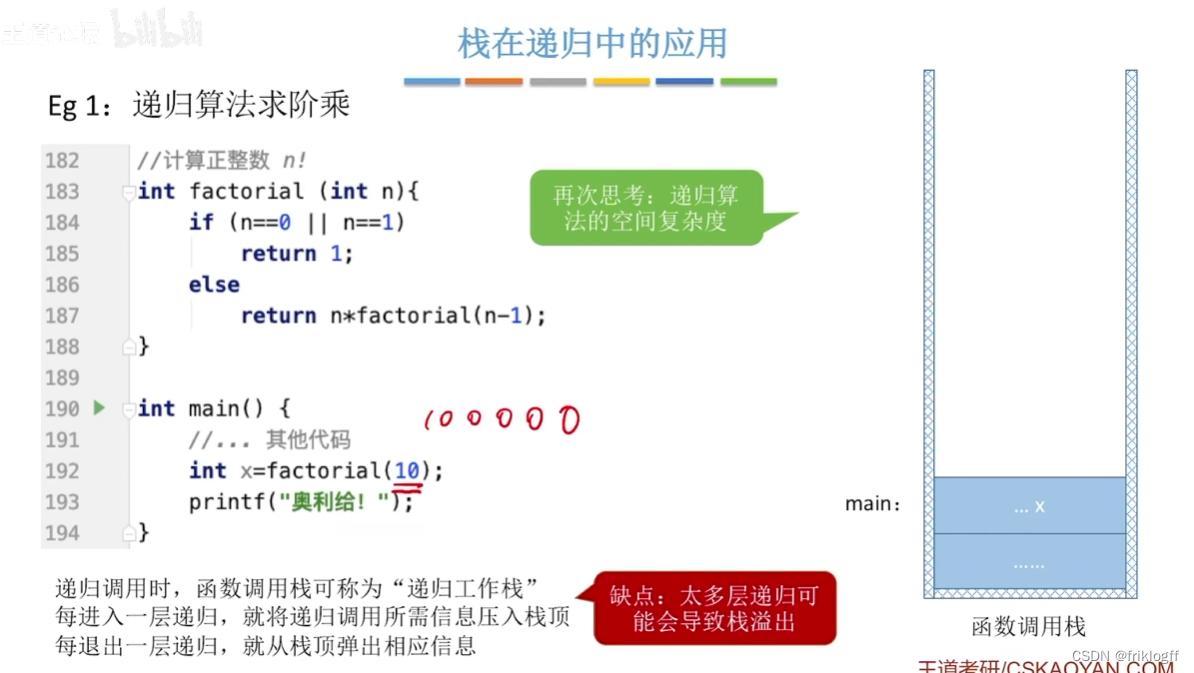
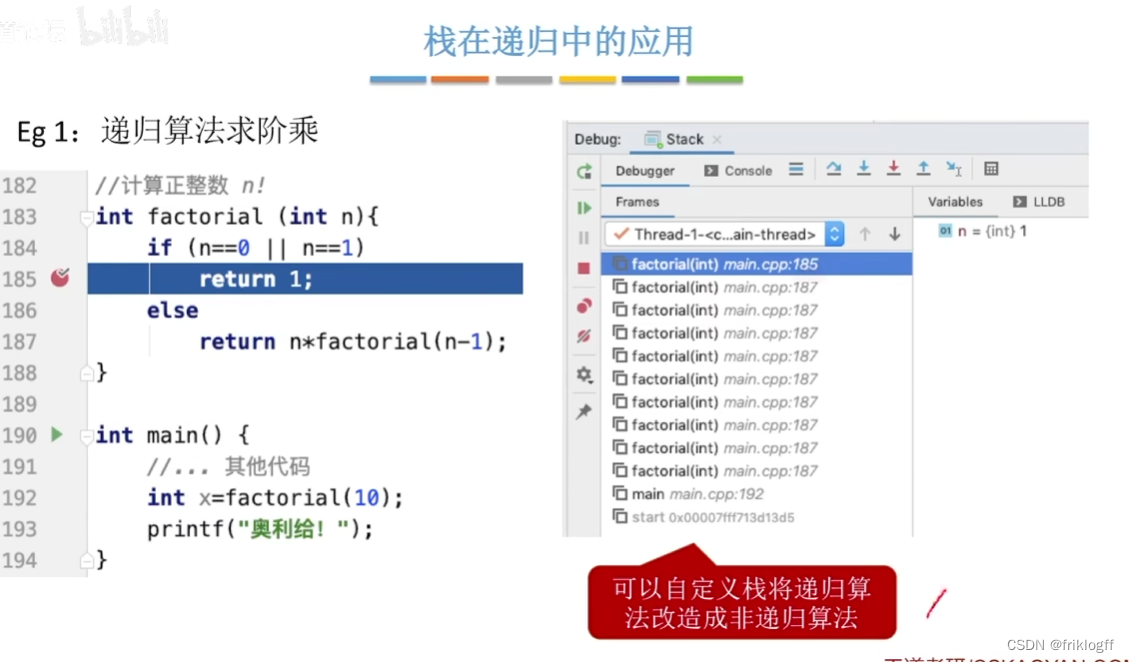
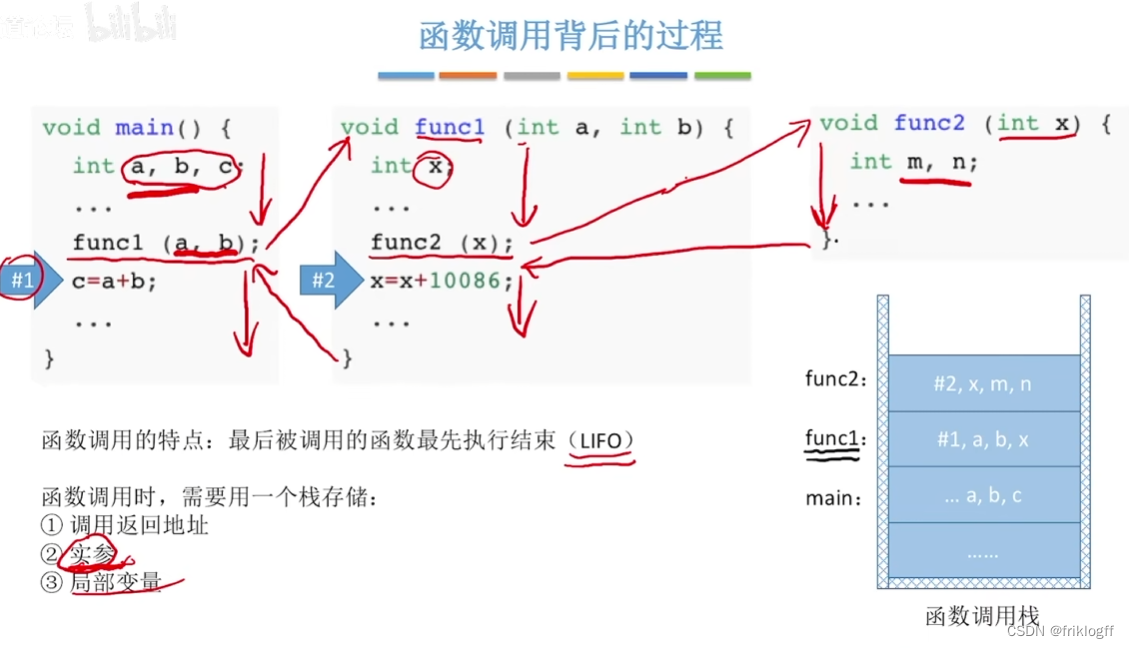
- 其他:数制转换、八皇后问题、行编辑程序、函数调用、迷宫求解等
小结

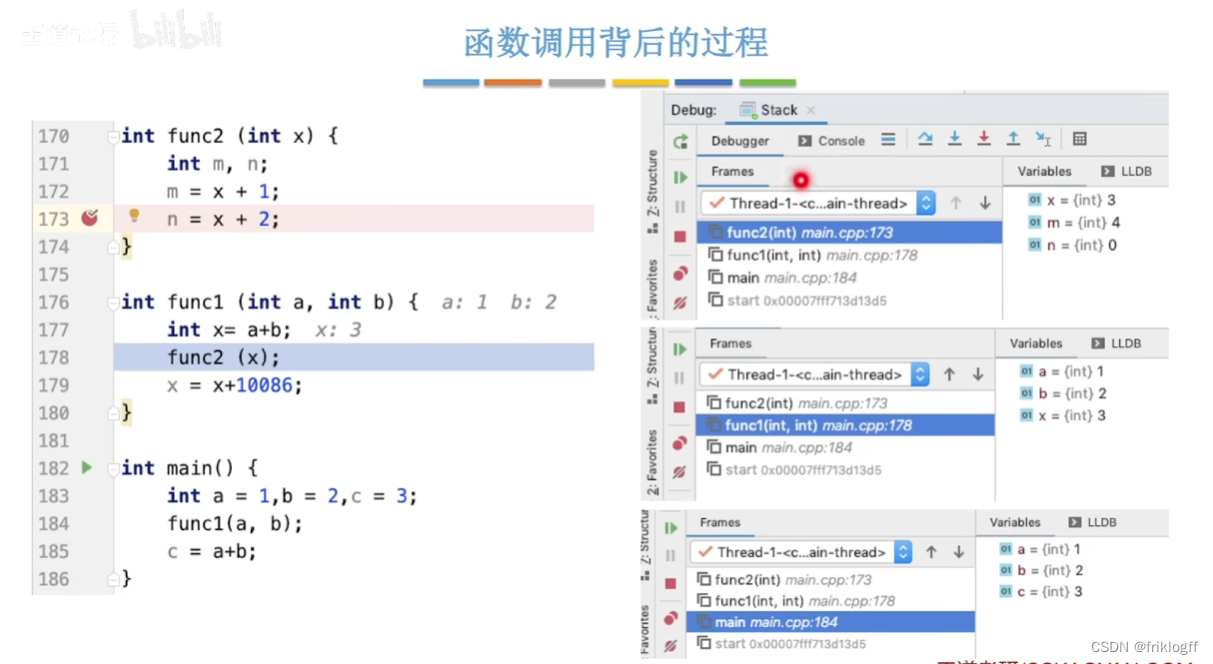
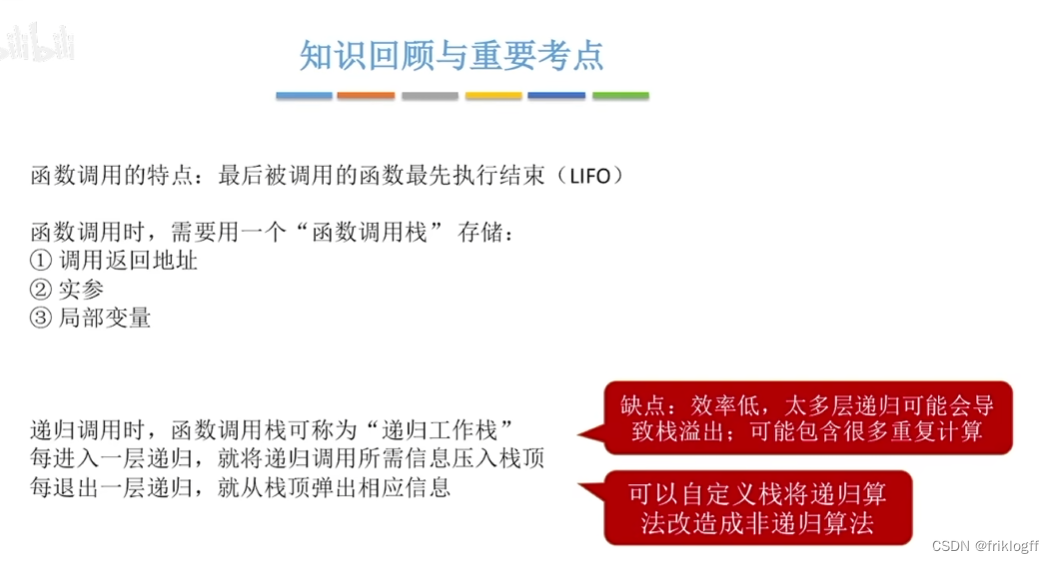
递归
-
概念
-
若对象部分地包含自己,或用自己给自己定义,则称这个对象是递归的
-
若一个过程直接或间接的调用自己,则这个过程是递归的
-
-
分治的思想:必备条件
-
能将一个问题转变成一个新问题,且两者的解法相同或类似,不同的仅是对象,且对象有变化规律
-
可以通过上述转化将问题化简
-
必须有一个明确的递归出口(递归边界)
-
-
形式

小结
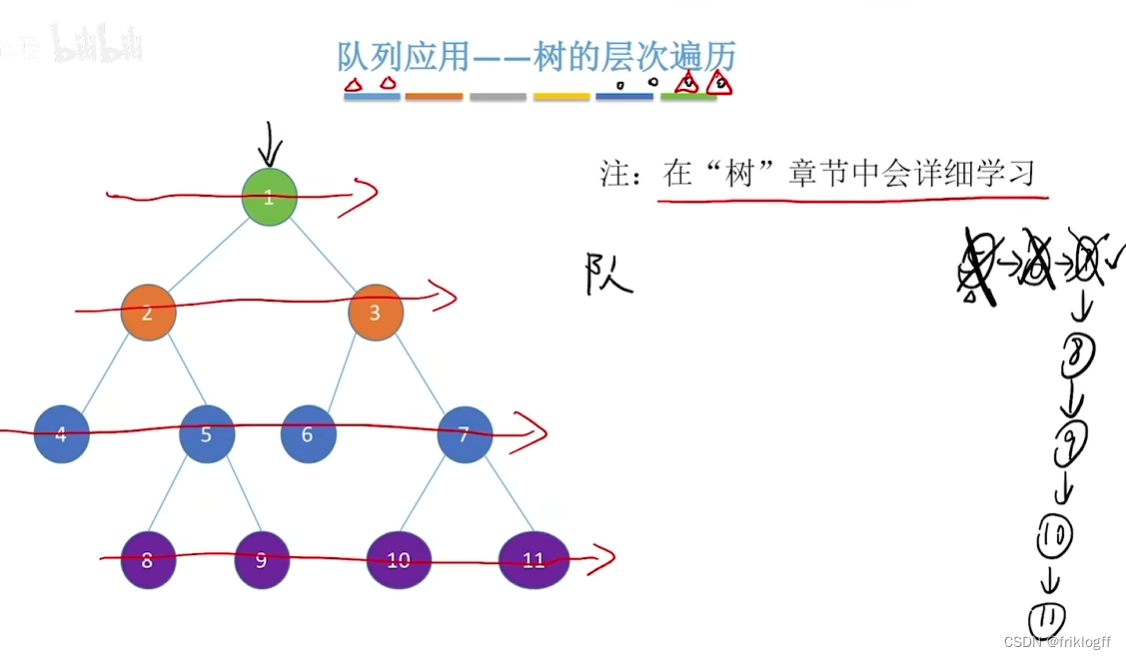
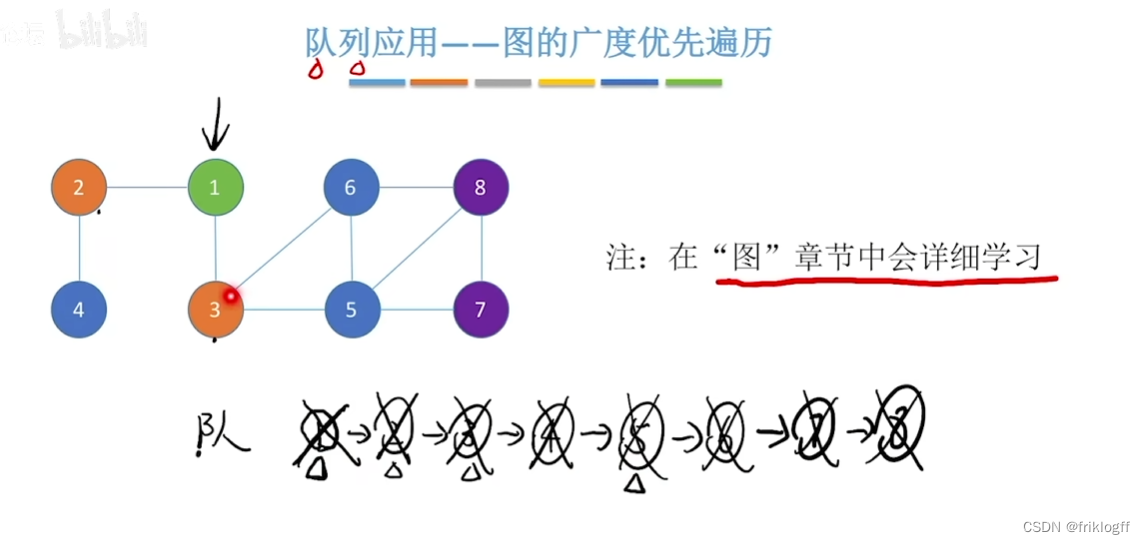
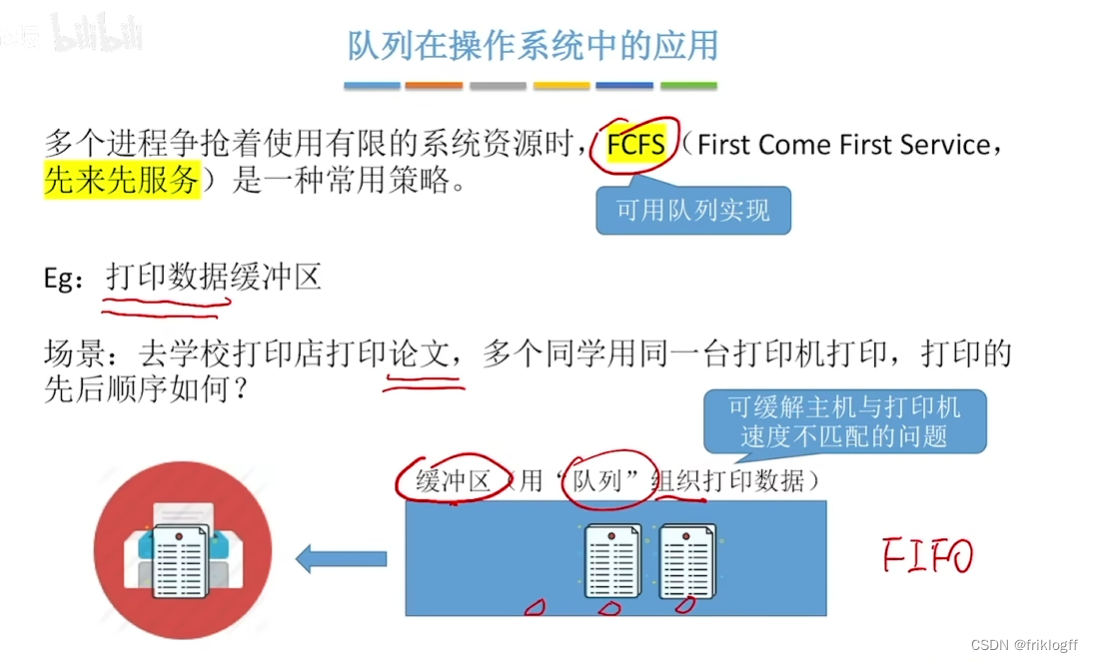
队列的应用
- 脱机打印输出、解决多用户引起的资源竞争问题、广度优先遍历、网络电文传输按时间先后顺序依次进行等等
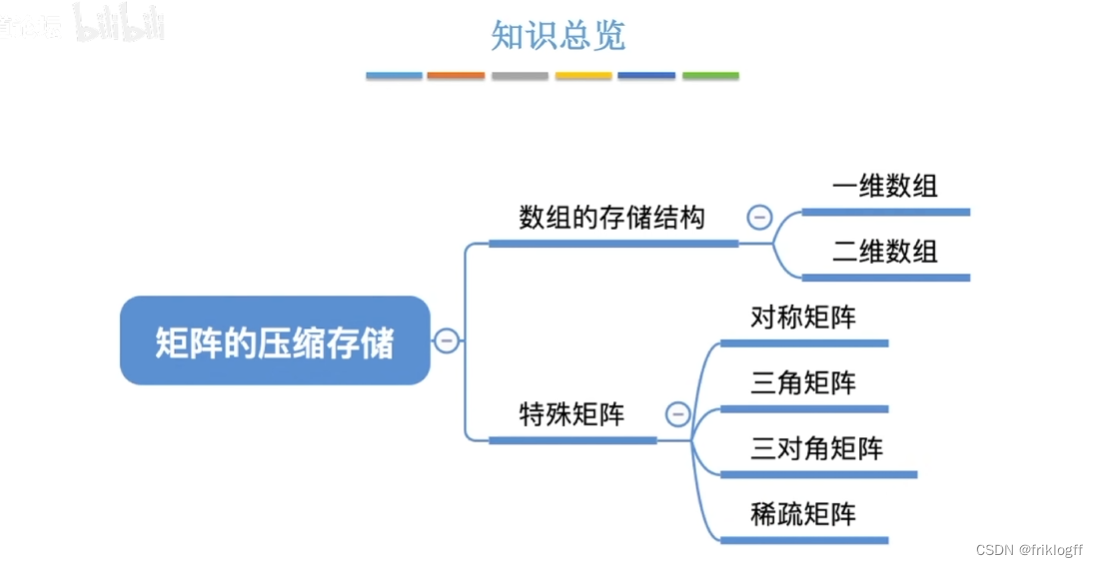
数组和特殊矩阵
本节的题目计算都可以不记公式,直接代入推导
数组
-
概念
- 数组是由n个相同类型的数据元素构成的有限序列,每个元素在n个线性关系中的序号称为元素下标,下标取值范围称为数组的维界
-
与线性表的关系
- 数组是线性表的推广,一维数组可视为一个线性表,二维数组可以视为其元素也是定长线性表的线性表
-
数组的存储结构
-
数组的所有元素在内存中占用一段连续的存储空间
-
一维数组
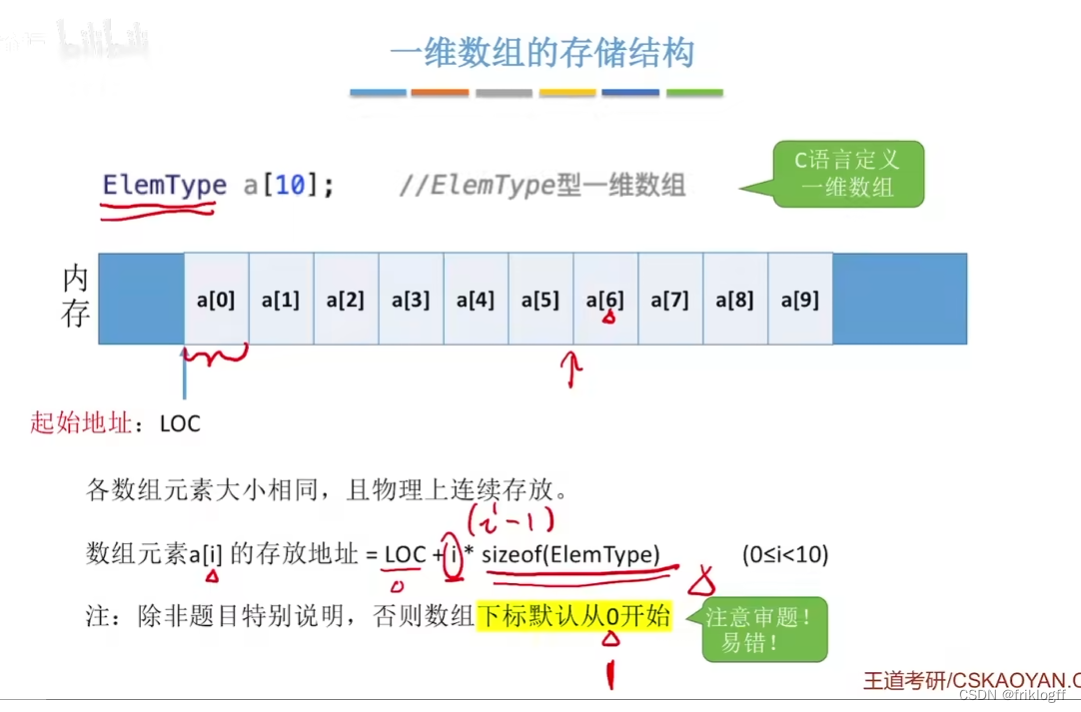
- 存储结构关系式:LOC(ai) = LOC(a0) + i × L (0 <= i < n,L是每个元素所占存储单元)
-
多维数组

-
按行优先(一行行存储)
- 存储结构关系式:LOC(ai,j) = LOC(a0,0) + [i × (h1 + l) + j] × L (二维数组:h1 × h2)
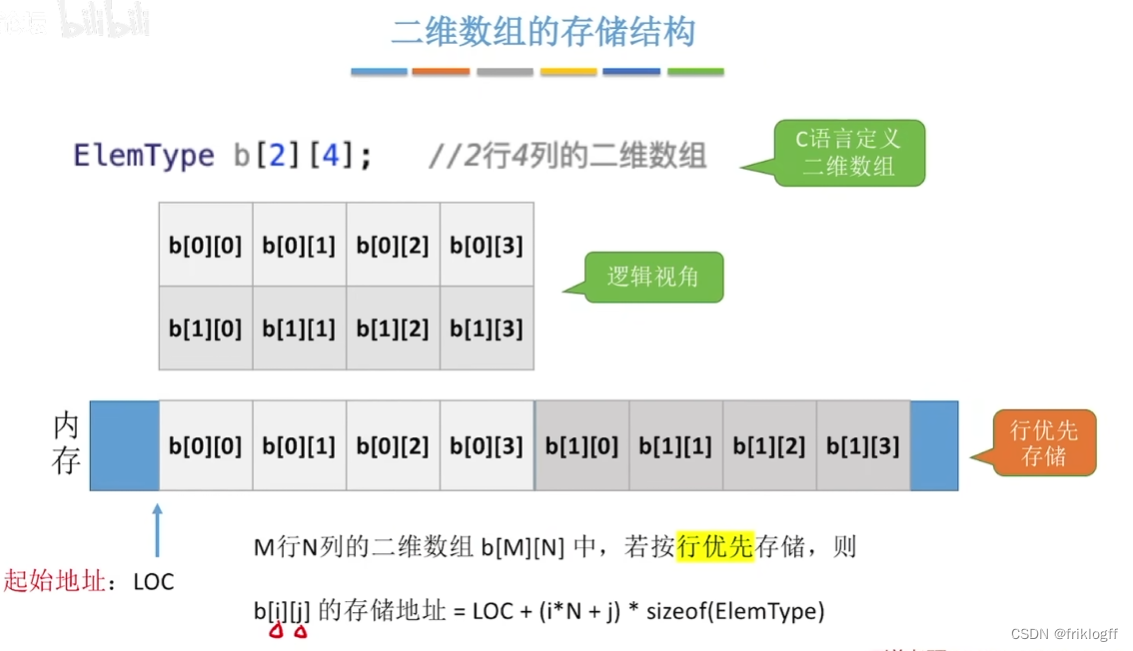
- 存储结构关系式:LOC(ai,j) = LOC(a0,0) + [i × (h1 + l) + j] × L (二维数组:h1 × h2)
-
按列优先(一列列存储)
- 存储结构关系式:LOC(ai,j) = LOC(a0,0) + [j × (h2 + l) + i] × L (二维数组:h1 × h2)

- 存储结构关系式:LOC(ai,j) = LOC(a0,0) + [j × (h2 + l) + i] × L (二维数组:h1 × h2)
-
-
特殊矩阵
-
指具有许多相同矩阵元素或0元素,并且这些相同矩阵元素或0元素的分布有一定规律
-
压缩矩阵
- 找出特殊矩阵中值相同的矩阵元素的分布规律,把那些呈现分布规律的、多个值相同的元素只分配一个存储空间,对0元素不分配空间
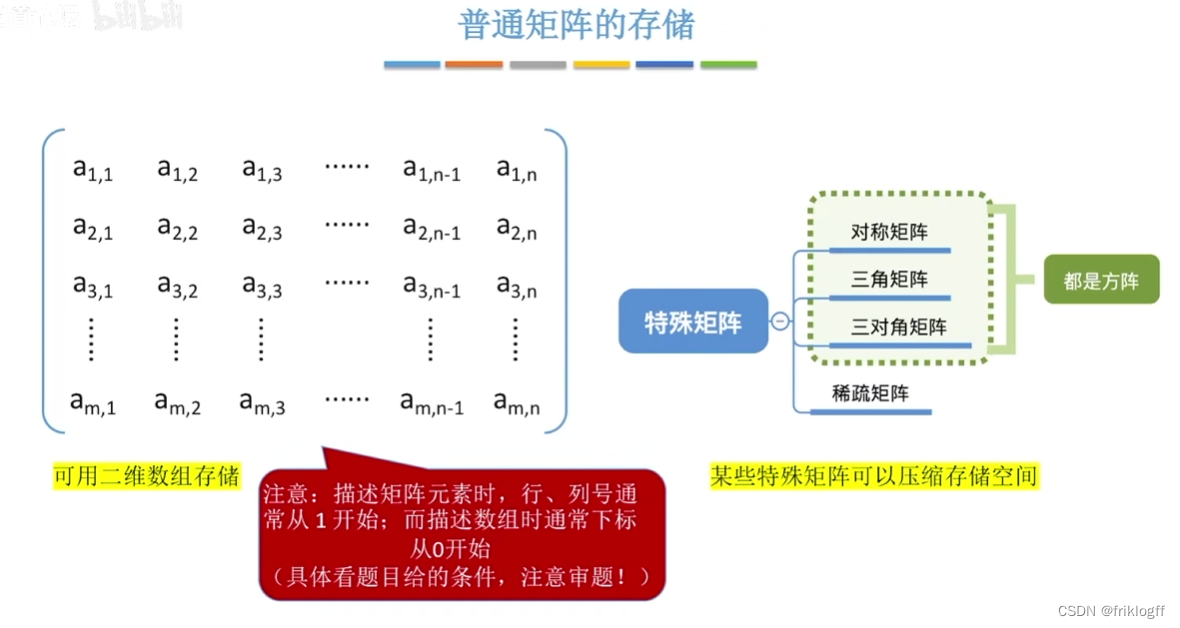
- 找出特殊矩阵中值相同的矩阵元素的分布规律,把那些呈现分布规律的、多个值相同的元素只分配一个存储空间,对0元素不分配空间
-
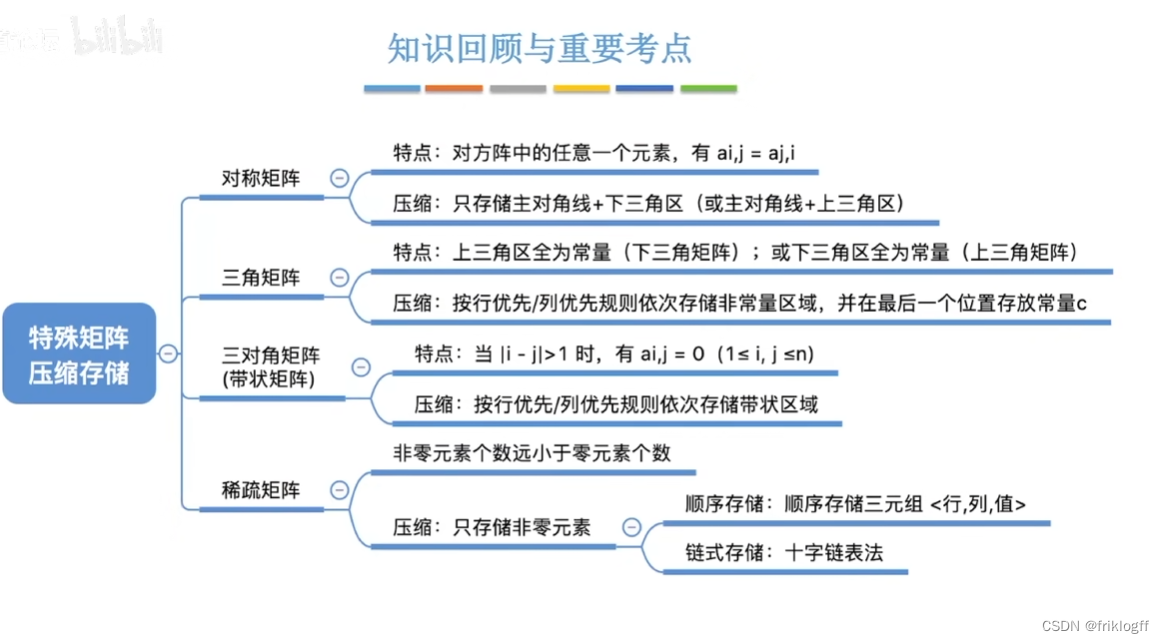
对称矩阵
-
概念
- 若对一个n阶方阵中的任意元素a(i, j) = a(j, i),则称其为对称矩阵,可放在一维数组B[n(n+1)/2]中
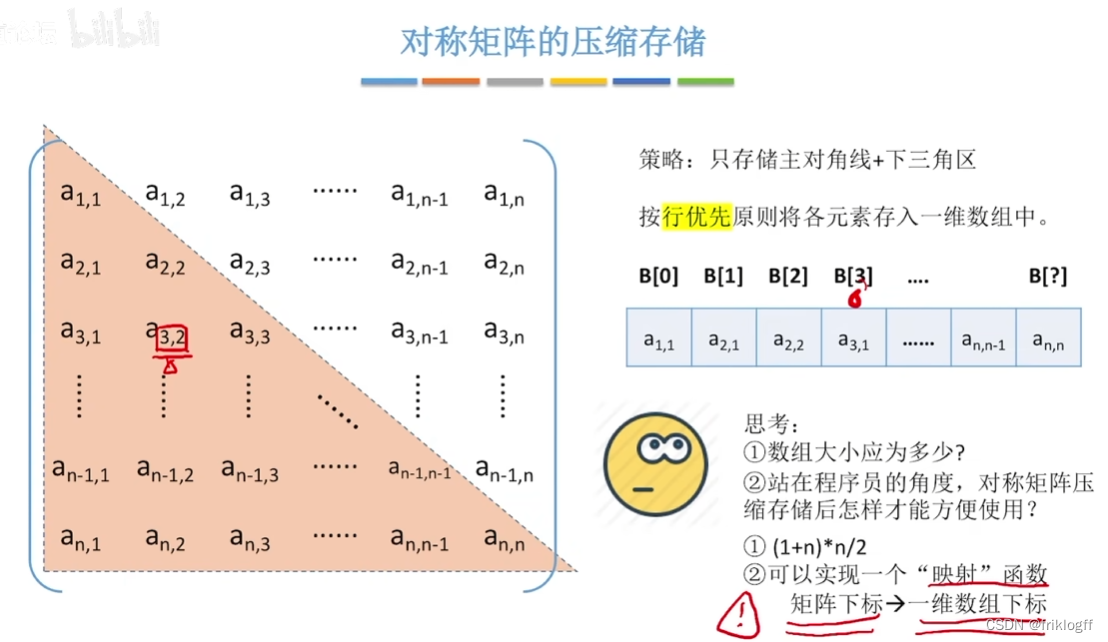
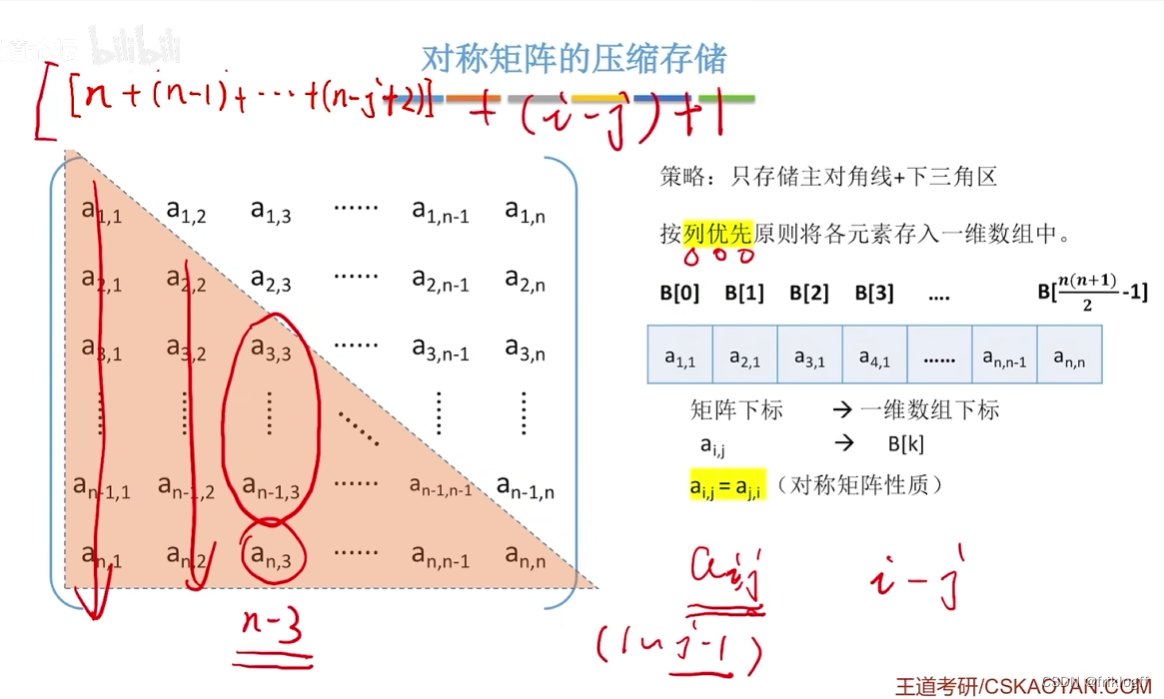
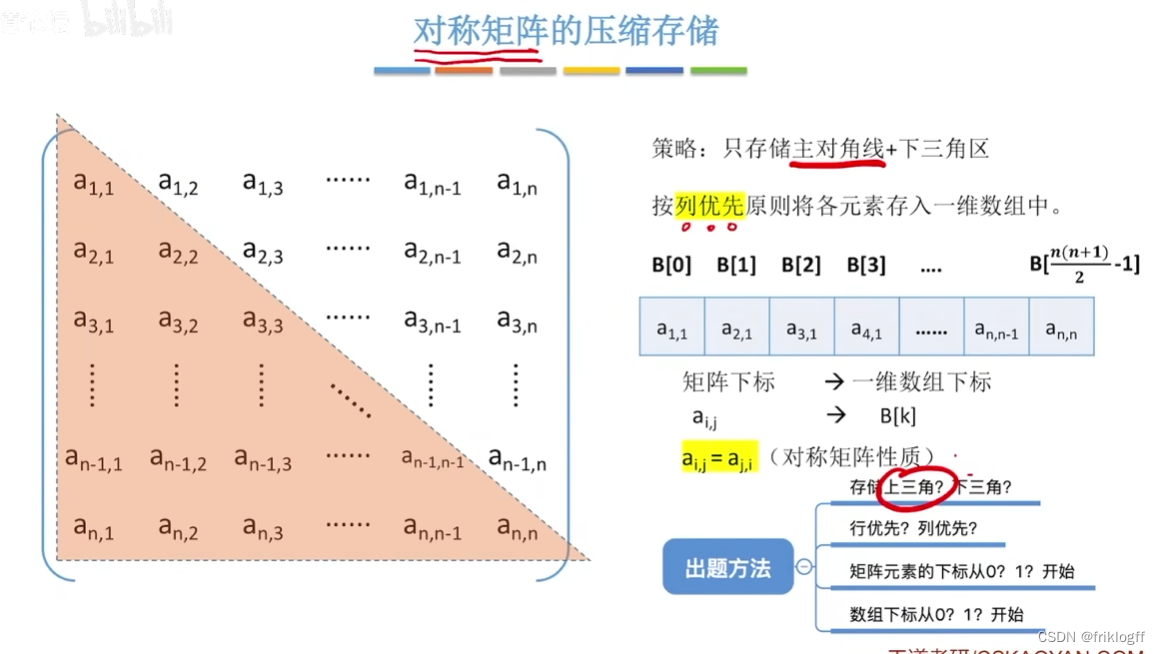
- 若对一个n阶方阵中的任意元素a(i, j) = a(j, i),则称其为对称矩阵,可放在一维数组B[n(n+1)/2]中
-
存储位置计算公式

-
-
三角矩阵
-
概念
- (上/下)三角区的所有元素均为同一常量,其可压缩为存储完(下/上)三角区和主对角线上元素 + 存储常量一次
-
(下/上)三角矩阵元素下标对应关系
-
下三角矩阵

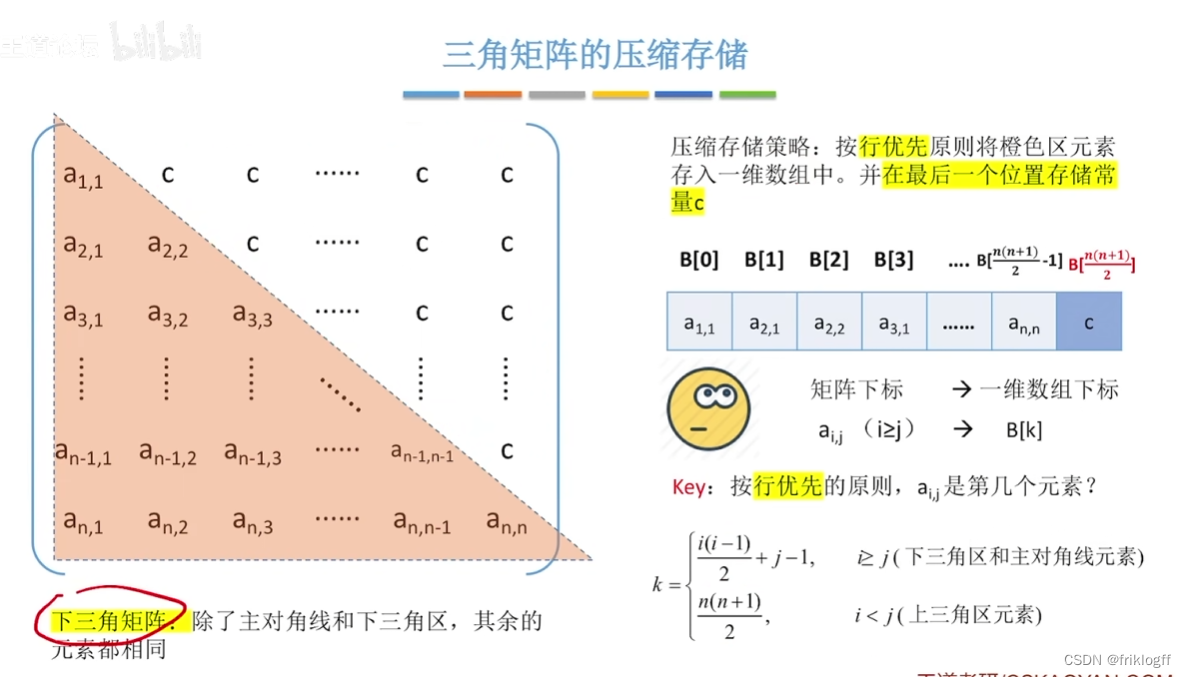
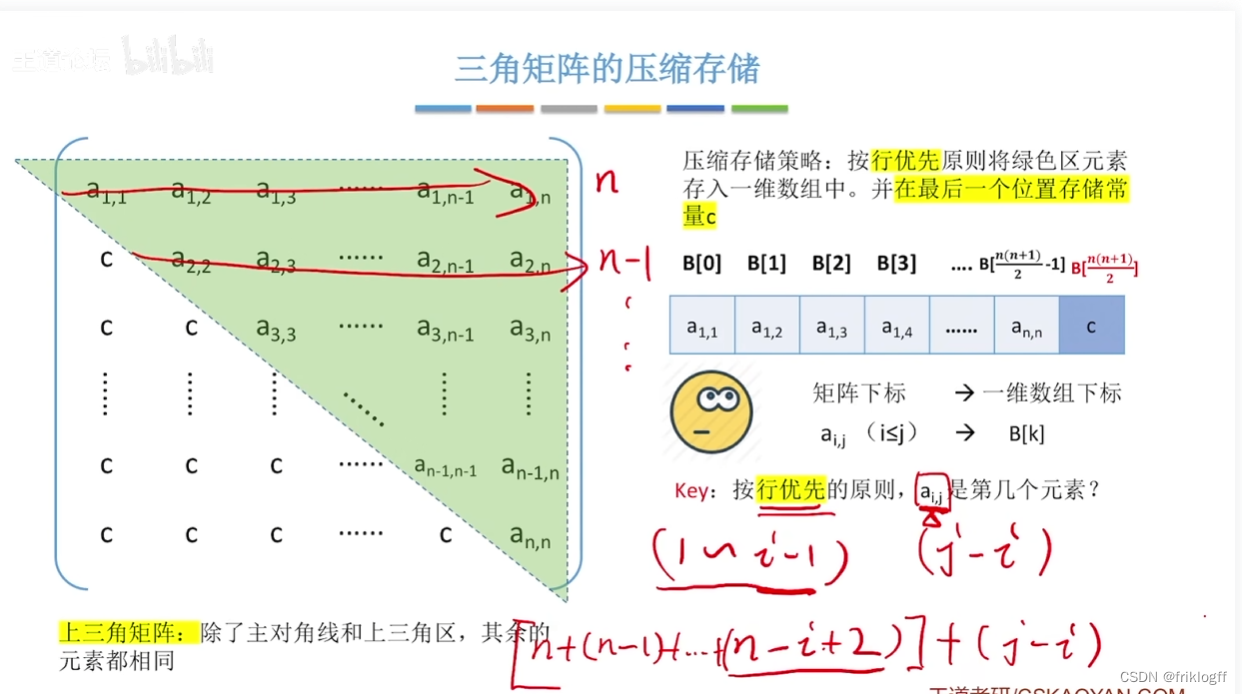
-
上三角矩阵
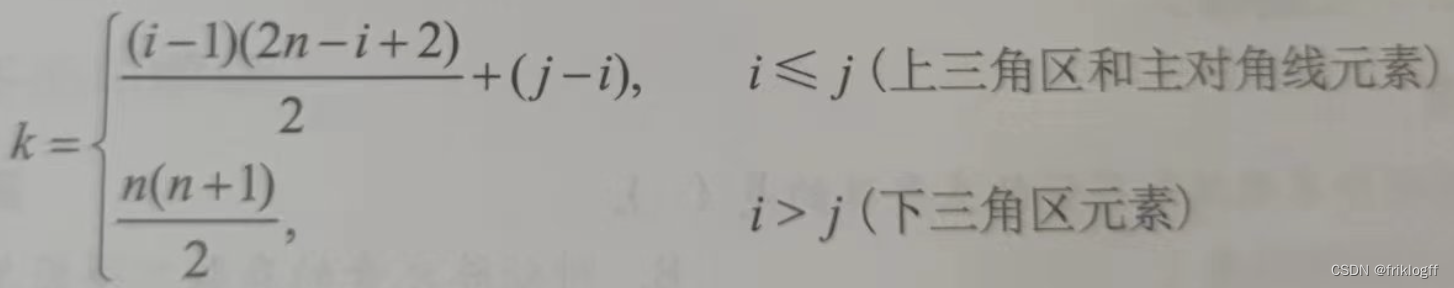
-
-
(下/上)三角矩阵在内存中的压缩存储形式
-
下三角矩阵

-
上三角矩阵

-
-
-
三对角矩阵
-
-
概念
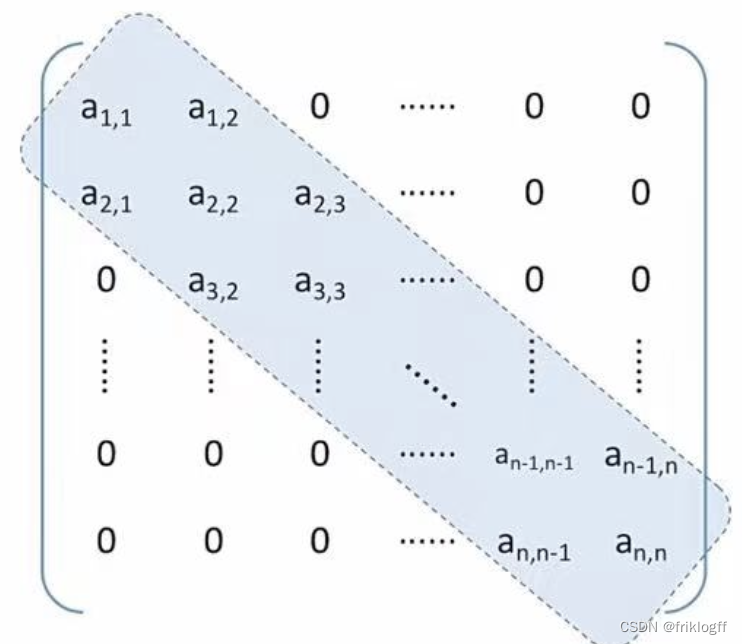
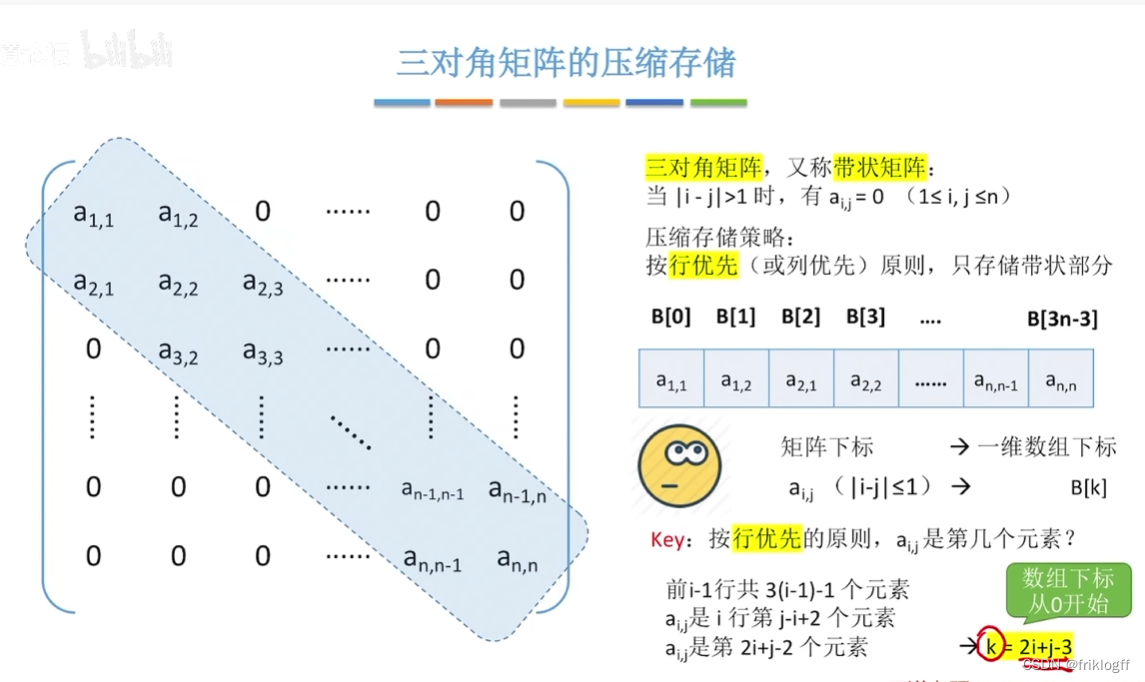
- 又称带状矩阵,除以对角线为中心的3条对角线区域外都为0
-
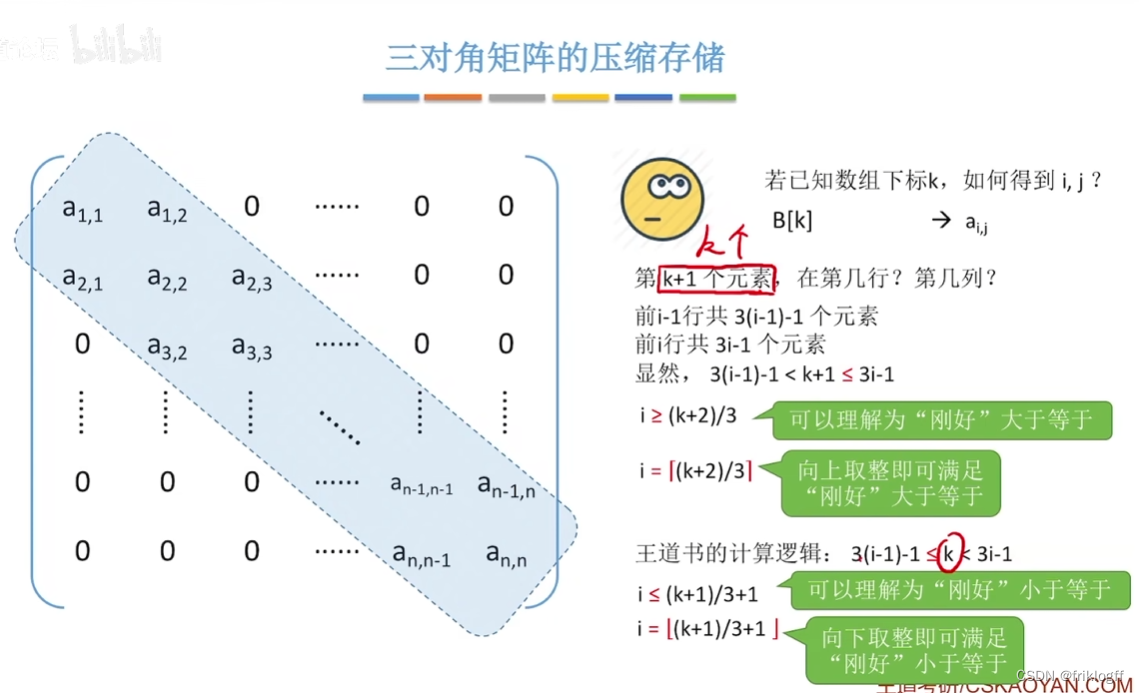
压缩存储:将元素按行优先方式存放在一维数组B中,且a(i, j)与B[n]对应关系为:k = 2i + j - 3
-
-
-
稀疏矩阵
-
概念
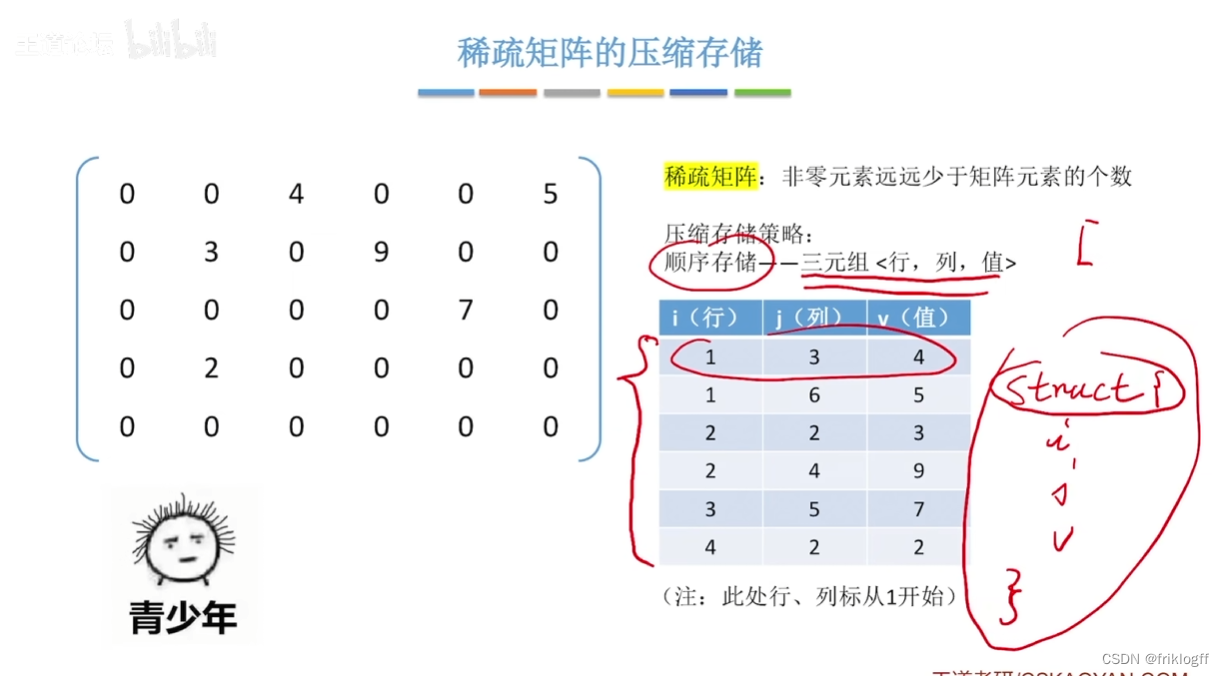
- 矩阵中非0元素的个数t,相对矩阵元素的个数s来说非常少,即s>>t
-
存储方式
-
三元组(行标、列标、值)
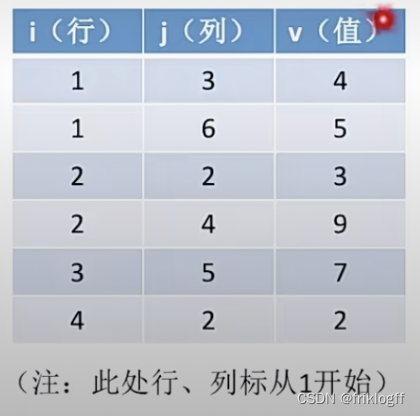
-
十字链表法
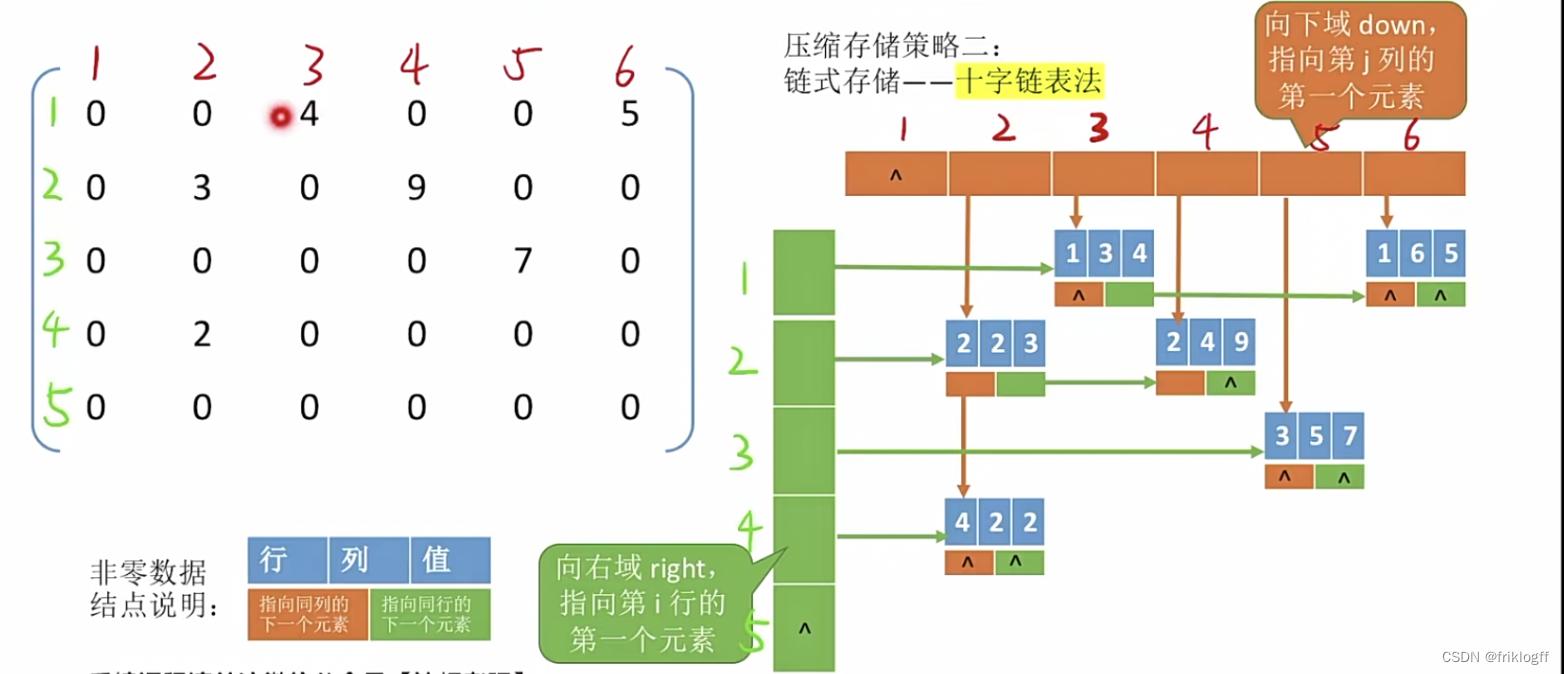
-
-
稀疏矩阵压缩存储后失去了随机存取的特性

-
补充代码
栈(数组模拟)
- 对数组简单操作,略
(循环)队列(数组模拟)
-
循环队列注意点:队满与队空条件需要有区别,即需要一个额外的元素空间判断队空与队满
void push_q(int x){if((tail + N + 1) % N != head){ //判断队满q[tail] = x;tail = (N + tail + 1) % N; //队尾插入一个数据注意指针移动需要%N,对头类似:head=(N+head+1)%N;}
}
bool empty(){ //判断是否为空return head == tail;
}
void pop_q(){ //对头删去一个元素if(!empty())head = (N + head + 1) % N;
}
void query(){ //查询对头元素if(!empty())printf("%d\n",q[head]);
}
单调栈
-
应用场景:求某个数左边第一个小于他的数;
思路:在每次暴力从for循环的当前值,向左遍历找第一个小于数的O(n2)情况下进行优化;
在向左遍历过程中删去无用的数(左边小于,但值大于),利用栈形成单调增大的序列,所求数即为栈顶; -
for(int i=0;i<n;i++){scanf("%d",&v);while(top&&s[top-1]>=v) top--; //去除比当前数大但在左边的数if(!top) printf("-1 ");else printf("%d ",s[top-1]); //输出栈顶元素,即第一个小于当前数的数s[top++]=v; //当前数压入栈中}
单调队列
-
应用场景:滑动窗口中最小值,也可优化背包问题;
思路:同理通过删去无用的数进行优化;
(求滑动窗口中最小值)队列头保留最小的数,遍历数组,若队尾数大于遍历的数则不断删去队尾(同理无用的数),使得队列单调增,在遍历过程中,不断更新队头使得不超过滑动窗口。 -
for(int i=0;i<n;i++){if(l<r&&i-q[l]>len-1) l++; //移动对头使不超过滑动窗口,为了实现,q数组存下标while(l<r&&v[q[r-1]]>=v[i]) r--; //弹出队尾无用数,因为会在队尾弹出不满足先进先出原则,事实上也不能叫单调队列q[r++]=i; //每次都入队一个if(i>=len-1) printf("%d ",v[q[l]]); }
考研真题
408 - 2023
(考研真题待更新)
这篇关于【数据结构】考研真题攻克与重点知识点剖析 - 第 3 篇:栈、队列和数组的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!