本文主要是介绍精讲连连看制作方法,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
程序的关键在于判断用户连续点击的两个图案能否消除。两个图片可以消除的条件有两个:- 图片相同
- 图片间连线的转角数不得超过2 。
而判断能否通过小于两个转角的路径连通的算法有两种:
- 分类判断法
- 以转角数为标准的广度优先搜索
下面对两种算法分别讨论。
- 分类判断法
这里实质上是一种递归的思想,要判断图片A与图片B能否通过一条有N个转角的路径相连,可以转化为判断能否找到图片C,C与A能直线相连,且C与B能用一条有N-1个转角的路径相连。若这样的图片C存在,那么A与B就可以通过一条有N个转角的路径相连。
根据转角数不得超过2个的规则,我们可以分为转角数分别为0个、1个、2个这三种情况分别讨论。
(1)0转角连通(直线连通):两个图片的纵坐标或横坐标相等,且两者连线间没有其他图案阻隔。
(2)一个转角连通:其实相当于两个图片划出一个矩形,这两个图片是一对对角顶点,另外两个顶点如果可以同时和这两个棋子直连,那就说明可以"一折连通"。见下图两个红色棋子的连通情况,右上角打叉的位置就是折点。

图1.一个转角连通
(3)两个转角连通: 判断图片A与图片B能否经过有两个转角的路径连通实质上可以转化为判断能否找到一个点C,这个C点与A可以直线连通,且C与B可以通过有两个转角的路径连通。若能找到这样一个C点,那么A与B就可以经过有两个转角的路径连通 。
判断是否经两个转角连通的算法需要做两个方向上的扫描:水平扫描和垂直扫描。
水平扫描。如下图所示,为了判断A,B能否通过2个转角连通,则从A开始在水平方向上向左右扫描,并判断经过的点能否与B点经过1个转角连通。显然C点能与B点经1个转角连通,故A,B能经2个转角连通。
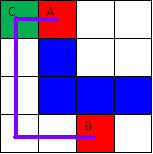
图2.两个转角连通的判断
垂直扫描。如下图所示,为了判断A,B能否通过2个转角连通,则从A开始在垂直方向上下扫描,并判断经过的点能否与B点经过1个转角连通。显然C点能与B点经1个转角连通,故A,B能经2个转角连通。
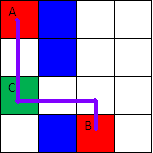
图3 .两个转角连通的判断
2.以转角数为基准的广度优先搜索法
这种算法参考《编程之美》。
这种算法的动机:若能将所有与图片A经过不多于2个转角的路径相连的图片找出来,加入一个集合S中。那么判断B与A能否相连只需判断B是否存在于集合S中即可。采用广度优先搜索算法可以方便的实现这一构想。算法的思路如下:
(1)定义空集S与T,将A加入集合S
(2)找出所有与A能直接相连的点,将其加入集合S
(3)找出与集合S中的点能直接相连的点,加入集合T,然后将T中所有元素加入到集合S中,清空集合T
(4)找出与集合S中的点能直接相连的点,加入集合T,然后将T中所有元素加入到集合S中
(5)若B在集合S中,则A,B可以相连。否则A,B不能相连
模仿图论中广度优先搜索的算法,可以写出以转角为基准的广度优先搜索的伪代码如下:
//判断图片A与图片B能否经过不多于2个转角的路径相连的算法bool Match( Picture A,Picture B )
{
Set< picture > S ; //已经搜索到的点的集合,集合S中每个元素与A都可以通过不多于个转角的路径连通
Set< picture > T ; //临时存储搜索到的点
将A加入到S中
int crossNum = 0 ; //用于记录当前搜索到节点的最大转角数
While( B 不在S 中&& crossNum < 3 )
{
for ( S 中每个元素e )
{
将所有与e能直线连通的点加入到集合T中
}
T中的所有元素加入到S中
crossNum ++ ;
}
if ( B 在S中)
return true ;
else
return false ;
}
实际编程实现这一算法时可以采取优化措施,不一定要搜索出所有与A转角不超过2的点。
本程序实现时采用了第一种算法。
这篇关于精讲连连看制作方法的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!