本文主要是介绍多元线性回归模型中的常数项,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
作者:flyerye链接:https://www.zhihu.com/question/22450977/answer/250476871
来源:知乎
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
回答这个问题,我们先从定义出发,然后再结合个实际例子去理解。从定义来看,多元线性回归方程定义如下:
这里的 a 为常数项, 为随机误差项,且服从标准正态分布(
),或者我们把它称作白噪声(white noise)。通过图像,我们可以很好理解常数项和随机误差的含义:
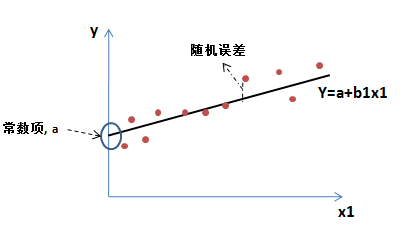 图一,一元线性回归示例
图一,一元线性回归示例 上图是多元线性回归回归的一个特例,即一元线性回归。多元就是在一元的基础上,用更多的自变量对因变量进行解释。我们以一元为例,来看常数项和随机误差的含义。从图中可以看出,常数项是拟合的一元回归直线在因变量(Y)轴上的截距;误差是实际的点和回归直线之间的差,而随机则表示的是这个误差不是固定的,有大有小,没有特定的规律,服从标准正态分布。具体来说,常数项表示的是未被自变量解释的且长期存在(非随机)的部分,即信息残留。而随机误差是在自变量解释空间内,预测值和去掉常数项的实际值的误差。下图是从一个多元线性回归模型的视角去看问题:因变量(Y)代表需要解释的全体信息,模型里的Xi构成的空间是自变量解释空间,随机误差存在于自变量解释空间中。在自变量解释空间外,如果还有恒定的信息残留,那么这部分信息构成常数项。
<img src="https://pic1.zhimg.com/50/v2-68beb4a4bd82ac547341ae0d5f123009_hd.jpg" data-rawwidth="283" data-rawheight="285" class="content_image" width="283"> 图二,多元线性回归模型解释因变量示意图
图二,多元线性回归模型解释因变量示意图 链接:https://www.zhihu.com/question/22450977/answer/21409955
来源:知乎
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
一言以蔽之,在计量经济学的线性回归模型中,常数项在很多情况下并无实际的解释意义。
要论含义,常数项的数学含义是,平均来讲,当所有解释变量的值为0的时候,被解释变量的值是几?但是在计量经济学的实证模型中,这通常是无意义的,原因很简单,因为在很多时候,解释变量的定义域并不一定包括0,比如人的身高、体重等等。可是,即便所有的解释变量都可以同时取0,常数项依然是基本无意义的。我们回到线性回归的本质上来讲的话,所有参数的确定都为了一个目的:让残差项的均值为0,而且残差项的平方和最小。所以,想象一下,当其他的参数都确定了以后,常数项的变化在图像上表现出来的就是拟合曲线的上下整体浮动,当曲线浮动到某一位置,使得在该位置上,残差项的均值为0,曲线与y轴所确定的截距即为常数项。因此,可以理解为常数项是对其他各个解释变量所留下的偏误(bias)的线性修正。但是要说常数项具体的值所代表的解释意义,在通常情况下是无意义的。
写到这里,有人可能会问,既然无意义,我们何不去掉常数项?答案是否定的,原因是,如果去除了常数项,就等于强制认定当所有解释变量为0时,被解释变量为0。如果这个断定不符合实际意义,而你执意去除常数项的话,你的线性估计将是有偏的。
随机误差项的理解相对简单,在线性回归模型中,每一个观测值都有一个残差项,也叫随机误差项,它刻画的是模型的估计值和真实观测值之间的偏差。
平狄克的「econometrics」书中提到过「可以将常数项看作是值恒为1的一个虚拟变量的系数」(上述原话为英文,但是是这个意思)也就是说,它可能包含了一些你忽视掉的虚拟变量。
而且带常数项的模型其实是对随机误差项的优化,我们在做OLS时总是假定随机误差项是标准正态分布的,但这很难满足。假设随机误差项的均值不是0,而是一个常数,那么加入常数项的模型就会使得随机误差项又变成了标准正态分布,它的期望就被含在常数项里了。总而言之,这样的模型更为靠谱。
作者:邹日佳
链接:https://www.zhihu.com/question/19664505/answer/12629408
来源:知乎
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
这篇关于多元线性回归模型中的常数项的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!








