POJ3608 Bridge Across Islands

2024-04-03 07:32
文章标签 bridge across islands poj3608

本文主要是介绍POJ3608 Bridge Across Islands，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

题目链接

问题分析

题意即求两个凸包间的最小距离。

一开始十分暴力地写了一个闵可夫斯基和，后来发现变种的旋转卡壳转一转就好了QAQ

闵可夫斯基和的思路十分简单，下面看一下旋转卡壳的做法：

1

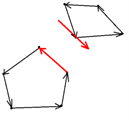
不难发现两个凸包间的最短距离一定像上图那样。所以我们只需要枚举一个凸包的边，找另一个凸包上的对踵点就好了。这个过程需要执行两次。

注意判断线段平行和求点到线段距离的细节。

参考程序

闵可夫斯基和版：

#include <cstdio>
#include <algorithm>
#include <cmath>
using namespace std;const int Maxn = 10010;
const double Eps = 1e-12;
struct point {double x, y;point() {}point( double _x, double _y ) : x( _x ), y( _y ) {}inline point operator + ( const point Other ) const {return point( x + Other.x, y + Other.y );}inline point operator - ( const point Other ) const {return point( x - Other.x, y - Other.y );}inline point operator * ( const double Other ) const {return point( x * Other, y * Other );}inline double operator * ( const point Other ) const {return x * Other.y - Other.x * y;}inline double operator / ( const point Other ) const {return x * Other.x + y * Other.y;}inline double Dis() const { return sqrt( x * x + y * y ); }
};
int N, M, L;
point A[ Maxn ], B[ Maxn ], C[ Maxn << 1 ], Base;inline int Cmp( double x, double y ) {if( fabs( x - y ) <= Eps ) return 0;if( x - y > Eps ) return 1;return -1;
}
inline bool Cmp1( point x, point y ) {return Cmp( ( x - Base ) * ( y - Base ), 0.0 ) == 1 || ( Cmp( ( x - Base ) * ( y - Base ), 0.0 ) == 0 && Cmp( ( x - Base ).Dis(), ( y - Base ).Dis() ) == -1 );
}
void Get( point *A, int &N ) {for( int i = 2; i <= N; ++i )if( Cmp( A[ i ].y, A[ 1 ].y ) == -1 || ( Cmp( A[ i ].y, A[ 1 ].y ) == 0 && Cmp( A[ i ].x, A[ 1 ].x ) == -1 ) )swap( A[ i ], A[ 1 ] );Base = A[ 1 ]; sort( A + 2, A + N + 1, Cmp1 );L = 1; C[ 1 ] = A[ 1 ];for( int i = 2; i <= N; ++i ) {for( ; L > 1 && Cmp( ( A[ i ] - C[ L - 1 ] ) * ( C[ L ] - C[ L - 1 ] ), 0.0 ) >= 0; --L );C[ ++L ] = A[ i ];}N = L; for( int i = 1; i <= L; ++i ) A[ i ] = C[ i ];return;
}
void Merge( point *A, int N, point *B, int M, point *C ) {L = 1; C[ 1 ] = A[ 1 ] + B[ 1 ];A[ ++N ] = A[ 1 ]; B[ ++M ] = B[ 1 ];int i1 = 1, i2 = 1;for( ; i1 < N && i2 < M; ) {if( Cmp( ( A[ i1 + 1 ] - A[ i1 ] ) * ( B[ i2 + 1 ] - B[ i2 ] ), 0.0 ) >= 0 ) {C[ L + 1 ] = C[ L ] + ( A[ i1 + 1 ] - A[ i1 ] ); ++L; ++i1;} else {C[ L + 1 ] = C[ L ] + ( B[ i2 + 1 ] - B[ i2 ] ); ++L; ++i2;}}for( ; i1 < N; ++i1 ) C[ L + 1 ] = C[ L ] + ( A[ i1 + 1 ] - A[ i1 ] ), ++L;for( ; i2 < M; ++i2 ) C[ L + 1 ] = C[ L ] + ( B[ i2 + 1 ] - B[ i2 ] ), ++L;return;
}
bool Check() {for( int i = 1; i < L; ++i )if( Cmp( C[ i + 1 ] * C[ i ], 0.0 ) > 0 ) return false;return true;
}
double GetDis( point A, point B, point C ) {point D = C + point( -( A - B ).y, ( A - B ).x );double T = ( D - A ) * ( C - A ) / ( ( C - B ) * ( D - B ) );if( Cmp( T, 0.0 ) <= 0 ) return min( A.Dis(), B.Dis() );point O = A * ( 1 / ( T + 1.0 ) ) + B * ( T / ( T + 1.0 ) );return ( O - C ).Dis();
}
int main() {scanf( "%d%d", &N, &M );while( N != 0 || M != 0 ) {for( int i = 1; i <= N; ++i ) scanf( "%lf%lf", &A[ i ].x, &A[ i ].y );for( int i = 1; i <= M; ++i ) scanf( "%lf%lf", &B[ i ].x, &B[ i ].y );for( int i = 1; i <= M; ++i ) B[ i ].x = -B[ i ].x, B[ i ].y = -B[ i ].y;Get( A, N ); Get( B, M );Merge( A, N, B, M, C );if( Check() ) printf( "0.000000\n" );else {double Ans = 1000000000.0;for( int i = 1; i < L; ++i ) Ans = min( Ans, GetDis( C[ i ], C[ i + 1 ], point( 0.0, 0.0 ) ) );printf( "%.6lf\n", Ans );}scanf( "%d%d", &N, &M );}return 0;
}

旋转卡壳版：

#include <cstdio>
#include <cmath>
#include <algorithm>
using namespace std;const int Maxn = 10010;
const double Eps = 1e-12;
struct point {double x, y;point() {}point( double _x, double _y ) : x( _x ), y( _y ) {}inline point operator + ( const point Other ) const {return point( x + Other.x, y + Other.y );}inline point operator - ( const point Other ) const {return point( x - Other.x, y - Other.y );}inline double operator * ( const point Other ) const {return x * Other.y - Other.x * y;}inline point operator * ( const double Other ) const {return point( x * Other, y * Other );}inline double Mod() const { return sqrt( x * x + y * y ); }
};
int N, M, Size;
point A[ Maxn ], B[ Maxn ], Base, Stack[ Maxn ];int Cmp( double x, double y ) {if( fabs( x - y ) <= Eps ) return 0;if( x - y > Eps ) return 1;return -1;
}
bool Cmp1( point X, point Y ) {return Cmp( ( X - Base ) * ( Y - Base ), 0.0 ) == 1 || ( Cmp( ( X - Base ) * ( Y - Base ), 0.0 ) == 0 && Cmp( ( X - Base ).Mod(), ( Y - Base ).Mod() ) == -1 );
}
void Graham( point *A, int &N ) {for( int i = 2; i <= N; ++i ) if( Cmp( A[ i ].y, A[ 1 ].y ) == -1 || ( Cmp( A[ i ].y, A[ 1 ].y ) == 0 && Cmp( A[ i ].x, A[ 1 ].x ) == -1 ) )swap( A[ i ], A[ 1 ] );Base = A[ 1 ]; sort( A + 2, A + N + 1, Cmp1 );Size = 1; Stack[ 1 ] = A[ 1 ];for( int i = 2; i <= N; ++i ) {for( ; Size > 1 && Cmp( ( A[ i ] - Stack[ Size - 1 ] ) * ( Stack[ Size ] - Stack[ Size - 1 ] ), 0.0 ) >= 0; --Size );Stack[ ++Size ] = A[ i ];}N = Size; for( int i = 1; i <= N; ++i ) A[ i ] = Stack[ i ];return;
}
inline int Pre( int N, int x ) { return ( x - 1 < 1 ) ? N : x - 1; }
inline int Suc( int N, int x ) { return ( x + 1 > N ) ? 1 : x + 1; }
inline double GetDis( point A, point B, point C ) {point D = C + point( -( B - A ).y, ( B - A ).x );double K = ( D - A ) * ( C - A ) / ( ( C - B ) * ( D - B ) );if( Cmp( K, 0.0 ) <= 0 ) return min( ( C - A ).Mod(), ( C - B ).Mod() );point O = A * ( 1.0 / ( K + 1.0 ) ) + B * ( K / ( K + 1.0 ) );return ( C - O ).Mod();
}
double Dis( point *A, int N, point *B, int M ) {int i1 = 1, i2; for( i2 = 1; i2 <= M; ++i2 )if( Cmp( ( A[ Suc( N, i1 ) ] - A[ i1 ] ) * ( B[ i2 ] - B[ Pre( M, i2 ) ] ), 0.0 ) == 1 &&Cmp( ( A[ Suc( N, i1 ) ] - A[ i1 ] ) * ( B[ Suc( M, i2 ) ] - B[ i2 ] ), 0.0 ) <= 0 )break;double Ans = GetDis( A[ Suc( N, i1 ) ], A[ i1 ], B[ i2 ] );if( Cmp( ( A[ Suc( N, i1 ) ] - A[ i1 ] ) * ( B[ Suc( M, i2 ) ] - B[ i2 ] ), 0.0 ) == 0 ) {i2 = Suc( M, i2 );Ans = min( Ans, GetDis( A[ Suc( N, i1 ) ], A[ i1 ], B[ i2 ] ) );}for( ++i1; i1 <= N; ++i1 ) {for( ; Cmp( ( A[ Suc( N, i1 ) ] - A[ i1 ] ) * ( B[ i2 ] - B[ Pre( M, i2 ) ] ), 0.0 ) <= 0 ||Cmp( ( A[ Suc( N, i1 ) ] - A[ i1 ] ) * ( B[ Suc( M, i2 ) ] - B[ i2 ] ), 0.0 ) == 1; i2 = Suc( M, i2 ) );Ans = min( Ans, GetDis( A[ Suc( N, i1 ) ], A[ i1 ], B[ i2 ] ) );if( Cmp( ( A[ Suc( N, i1 ) ] - A[ i1 ] ) * ( B[ Suc( M, i2 ) ] - B[ i2 ] ), 0.0 ) == 0 ) {i2 = Suc( M, i2 );Ans = min( Ans, GetDis( A[ Suc( N, i1 ) ], A[ i1 ], B[ i2 ] ) );}}return Ans;
}
int main() {scanf( "%d%d", &N, &M );for( ; N != 0 || M != 0; scanf( "%d%d", &N, &M ) ) {for( int i = 1; i <= N; ++i ) scanf( "%lf%lf", &A[ i ].x, &A[ i ].y );for( int i = 1; i <= M; ++i ) scanf( "%lf%lf", &B[ i ].x, &B[ i ].y );Graham( A, N ); Graham( B, M );printf( "%.6lf\n", min( Dis( A, N, B, M ), Dis( B, M, A, N ) ) );}return 0;
}

转载于:https://www.cnblogs.com/chy-2003/p/11329962.html

这篇关于POJ3608 Bridge Across Islands的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！


http://www.chinasem.cn/article/872280。

相关文章

Stripe data files across multiple physical devices and locations

Stripe data files across multiple physical devices and locations

Stripe data files across multiple physical devices and locations 如果在没有做条带的磁盘(即从存储到OS没有做raid)，那么就需要手工去做I/O的分布。切记，不应该将频繁使用的table和其index分开，这样会正大I/O； 针对tables、indexes、temp tablespace，首先调优SQL，其次如果真心无法再
阅读更多...
《GOF设计模式》—桥接（BRIDGE）—Delphi源码示例：可移植的用户界面

《GOF设计模式》—桥接（BRIDGE）—Delphi源码示例：可移植的用户界面

 示例：可移植的用户界面 说明：   代码：   unit uWindow;   interface   uses Windows,SysUtils,Classes,Graphics;   type     TWindow = class;     TWindowImp = class;       {窗口视图}     TView = class
阅读更多...
Linux 虚拟网络三大基石：Namespace、Veth pair 与 Bridge

Linux 虚拟网络三大基石：Namespace、Veth pair 与 Bridge

引言 在 Linux 的世界里，虚拟网络技术是系统管理、云计算和容器化不可或缺的一部分。今天，我们将深入探讨构建这些虚拟网络的三大基石：Namespace、Veth 对和 Bridge，揭示它们如何在背后默默支撑起你的网络环境。 Namespace：隔离与抽象的艺术 当我们谈起 Namespace，实际上是在讨论一种革命性的资源隔离机制。它让每个进程仿佛拥有一套独立的系统资源。通过将全局资
阅读更多...
设计模式：桥接模式（Bridge）

设计模式：桥接模式（Bridge）

欢迎支持笔者新作：《深入理解Kafka:核心设计与实践原理》和《RabbitMQ实战指南》，同时欢迎关注笔者的微信公众号：朱小厮的博客。 欢迎跳转到本文的原文链接：https://honeypps.com/design_pattern/bridge/ 定义：将抽象部分与它的实现部分分离，使它们都可以独立地变化。 意图：将抽象与实现解耦。  桥接模式主要应对的是由于实际的需要，某个类具
阅读更多...
PHP通过php-java-bridge调用…

PHP通过php-java-bridge调用…

受教了 原文地址：PHP通过php-java-bridge调用Java类中方法 作者：珍惜一切 今天偶在论坛里看见有人在问怎样配置通过 php-java-bridge调用Java类中的方法，刚好自己也在看这方面的东西，遂动手实现一番。由于没在公司，家里电脑又跟蜗牛爬一样慢【不开虚拟机，开了那还不爬死去。。。】，只测试win下的调用，为保险起见待在 linux上测试了再发linux的配置上来。
阅读更多...
【Java设计模式】Bridge模式：在Java中解耦抽象与实现

【Java设计模式】Bridge模式：在Java中解耦抽象与实现

文章目录 【Java设计模式】Bridge模式：在Java中解耦抽象与实现一、概述二、Bridge设计模式的别名三、Bridge设计模式的意图四、Bridge模式的详细解释及实际示例五、Java中Bridge模式的编程示例六、Bridge模式类图七、Java中何时使用Bridge模式八、Java中Bridge模式的实际应用九、Bridge模式的优点和权衡十、源码下载 【Java设
阅读更多...
cv_bridge中的编码模式与实现

cv_bridge中的编码模式与实现

image_encodings.cpp文件是关于图像编码模式的源文件，其中规定了RGB的图像以及深度图的编码模式   该编码文件image_encodings.cpp所依赖的头文件图 命令空间  sensor_msgs::image_encodings 下的函数 Functions int bitDepth (const std::string &encoding)bool hasA
阅读更多...
libvirt bridge network configure

libvirt bridge network configure

If you want to configure all the parameters of your virtual machine, you can issue the command like this: virsh edit ubuntu22.04-test In the GUI of NIC configuration, you can choose a configurati
阅读更多...
深入解析Linux Bridge：原理、架构、操作与持久化配置

深入解析Linux Bridge：原理、架构、操作与持久化配置

一、引言 在计算机网络中，桥接技术扮演着至关重要的角色，它能够实现不同网络设备之间的数据交换与共享。Linux Bridge作为Linux内核提供的一种网络功能，允许用户通过软件方式将多个网络接口桥接在一起，形成一个透明的二层网络。本文将从技术角度深入解析Linux Bridge的原理、架构以及常见的操作方式，并探讨如何实现桥接的持久化配置。 二、Linux Bridge的功能 简单来说，桥
阅读更多...
Number of Islands问题及解法

Number of Islands问题及解法

问题描述： Given a 2d grid map of '1's (land) and '0's (water), count the number of islands. An island is surrounded by water and is formed by connecting adjacent lands horizontally or vertically. You
阅读更多...

Copyright China编程 23002807@qq.com

沪ICP备2023033072号-2