本文主要是介绍excel统计分析——两向分组资料的协方差分析,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
参考资料:生物统计学
两向分组资料,是含协变量无重复观测值的两因素方差分析资料,协方差分析的步骤与单向分组资料的完全相同,只是进行平方和与自由度的分解时,处理部分需分解为两项。
若试验设有k个处理,每个处理n个重复,则kn对观测值可以按两向进行分组,其数据一般模式如下:
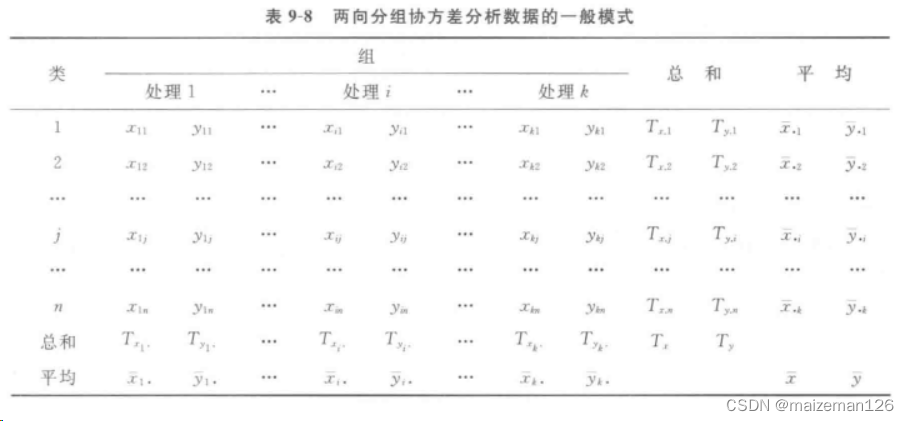
与两因素方差分析平方和的分解类似,总乘积和分解为三部分:
分析案例如下:
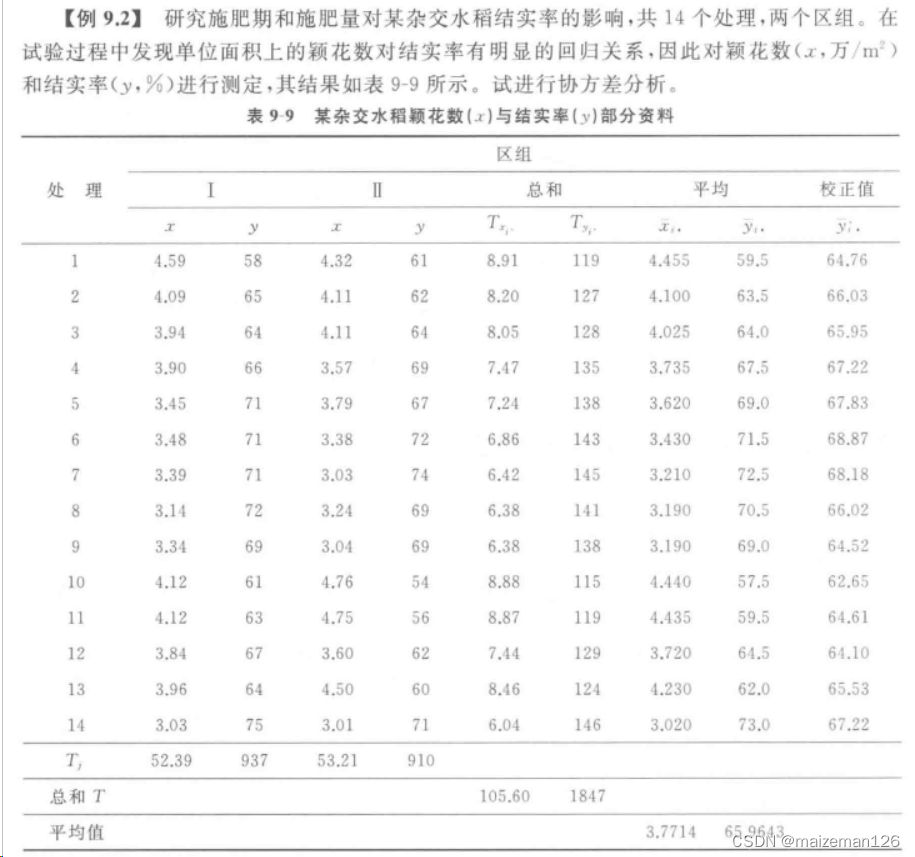
1、计算平方和与乘积和
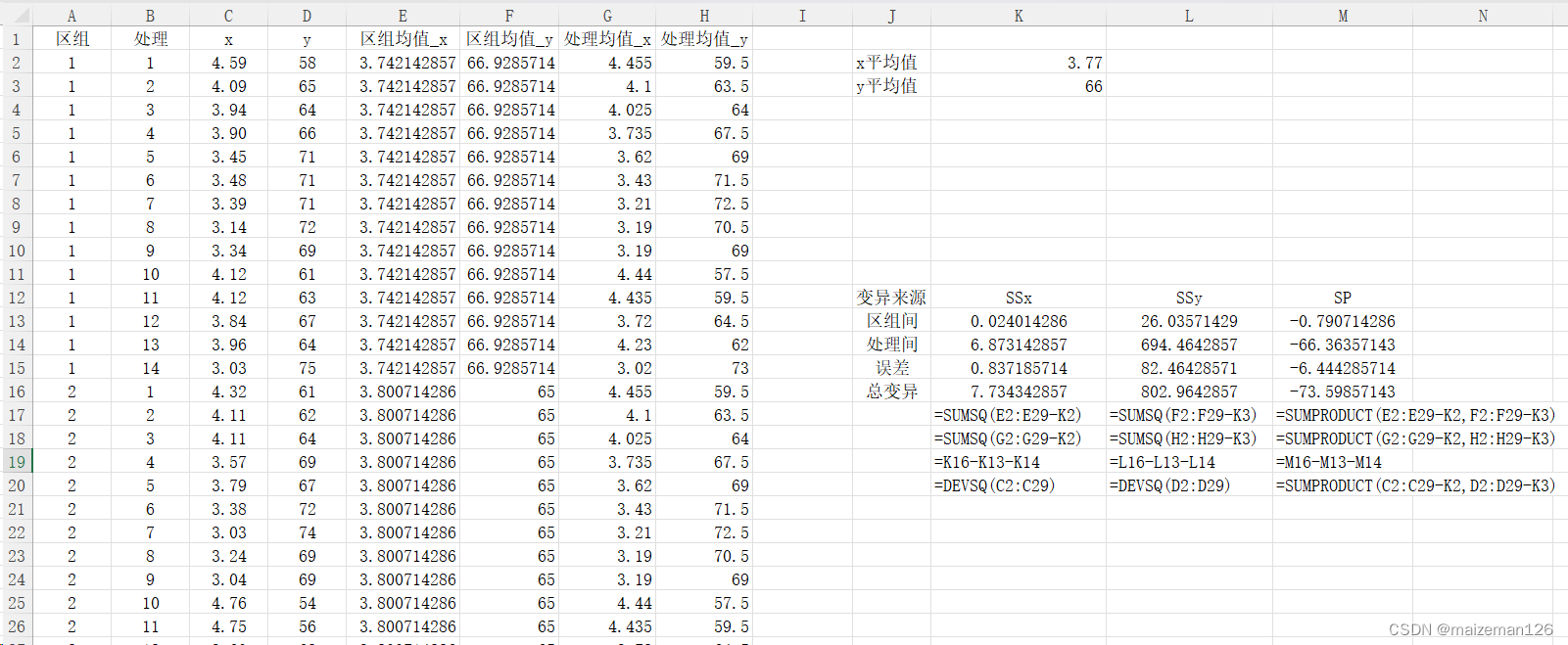
2、方差分析
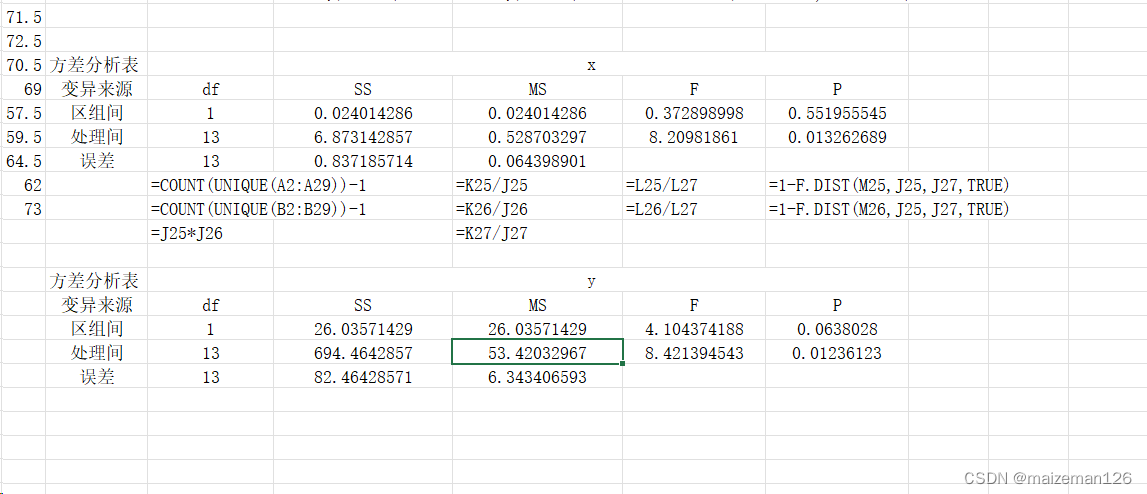
方差分析结果表示:不同区组间的x和y均无显著差异,但不同处理间的x和y差异均为极显著。
若y和x无关,则上述推断是正确的;如果y和x有关,则不一定正确。因此,首先应明确y和x有无线性关系。
3、线性回归分析
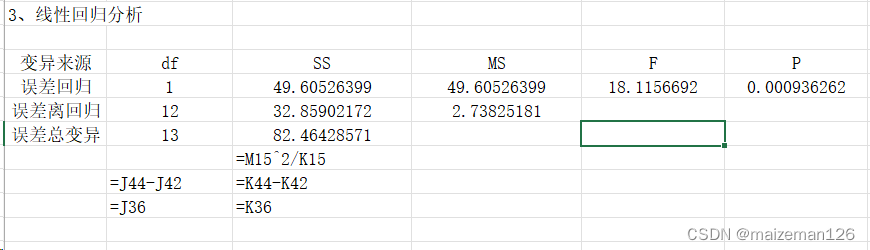
回归分析结果显示:y与x存在显著的线性回归关系,因此需要对y值进行矫正,并对矫正平均数进行显著性检验,才能确定不同区组或处理对y的效应。
4、矫正平均数的显著性检验
检验处理的矫正平均数的差异显著性时,需将处理间和误差项的df、SS和SP相加以代替总df、SS和SP;
检验区组的矫正平均数的差异显著性时,需将区组间和误差项的df、SS和SP相加以代替总df、SS和SP。
区组只是局部控制的一种手段,在结果分析上只需剔除其影响,而不必对其效应进行研究,因此这里仅对处理的矫正平均之间的差异显著性进行检验。
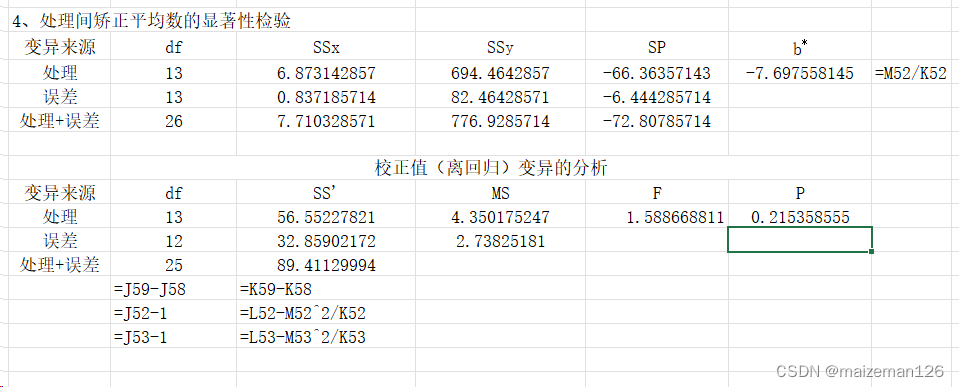
虽然我们可以通过误差项回归系数来计算出各处理的矫正平均数,即:
。但由于我们显著性检验结果显示处理间差异未达到显著性水平,说明各处理矫正平均数之间无显著差异,因而不需要再对各校正平均数间进行多重比较。
这篇关于excel统计分析——两向分组资料的协方差分析的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







