【自学记录】【Pytorch2.0深度学习从零开始学 王晓华】第四章 深度学习的理论基础

本文主要是介绍【自学记录】【Pytorch2.0深度学习从零开始学 王晓华】第四章 深度学习的理论基础，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

4.3.5 反馈神经网络原理的Python实现

遇到的疑问：

1、对神经网络前向计算中，关于系数矩阵W的讨论。

上一章讲到了层结构是【out,in】,所以我觉得在计算Y=WX+b的时候，W矩阵也应该是【out,in】的形状。但是该代码（或者正规代码实现流程）不是的，他是一个这样的结构：


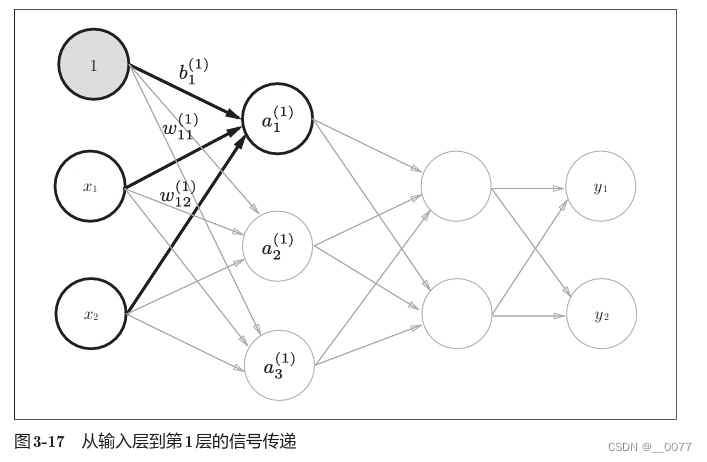
所以，W矩阵还是【in,out】结构，a1=X1W11+X2W12+b1,为了计算a1，会以列优先循环W矩阵：

 for j in range(self.hidden_n):total = 0.0for i in range(self.input_n):total += self.input_cells[i] * self.input_weights[i][j] #列优先循环W矩阵          

以上self.input_weights[i][j]代码：
j=1,依次输出(1,1),(2,1),对应W11，W12
j=2,依次输出(1,2),(2,2),对应W21，W22
j=3,依次输出(1,3),(2,3),对应W31，W32

以下是神经网络前向传播函数：

 def predict(self,inputs):for i in range(self.input_n - 1):self.input_cells[i] = inputs[i]for j in range(self.hidden_n):total = 0.0for i in range(self.input_n):total += self.input_cells[i] * self.input_weights[i][j]self.hidden_cells[j] = sigmoid(total)for k in range(self.output_n):total = 0.0for j in range(self.hidden_n):total += self.hidden_cells[j] * self.output_weights[j][k]self.output_cells[k] = sigmoid(total)return self.output_cells[:]#浅拷贝

2、有关self.output_cells[:]浅拷贝

神经网络前向传播函数最后使用 return self.output_cells[:] 而不是 return self.output_cells 的主要目的是返回 self.output_cells 的一个浅拷贝（shallow copy），而不是原始对象的引用。这意味着调用者将获得输出值的一个新列表，而不是对原始列表的引用。这可以确保原始 self.output_cells 列表的内部状态在函数返回后不会被意外修改，从而保持对象的封装性和数据的安全性。

源码\第四章\4_3.py

import numpy as np
import math
import random
def rand(a, b):return (b - a) * random.random() + a
def make_matrix(m,n,fill=0.0):mat = []for i in range(m):mat.append([fill] * n)return mat
def sigmoid(x):return 1.0 / (1.0 + math.exp(-x))
def sigmod_derivate(x):return x * (1 - x)
class BPNeuralNetwork:def __init__(self):self.input_n = 0self.hidden_n = 0self.output_n = 0self.input_cells = []self.hidden_cells = []self.output_cells = []self.input_weights = []self.output_weights = []def setup(self,ni,nh,no):self.input_n = ni + 1 #+1是加了一个隐藏层self.hidden_n = nhself.output_n = noself.input_cells = [1.0] * self.input_nself.hidden_cells = [1.0] * self.hidden_nself.output_cells = [1.0] * self.output_nself.input_weights = make_matrix(self.input_n,self.hidden_n)####这里，权重矩阵设定的是【in，out】self.output_weights = make_matrix(self.hidden_n,self.output_n)####这里，权重矩阵设定的是【in，out】# random activatefor i in range(self.input_n):for h in range(self.hidden_n):self.input_weights[i][h] = rand(-0.2, 0.2)for h in range(self.hidden_n):for o in range(self.output_n):self.output_weights[h][o] = rand(-2.0, 2.0)def predict(self,inputs):for i in range(self.input_n - 1):self.input_cells[i] = inputs[i]for j in range(self.hidden_n):total = 0.0for i in range(self.input_n):total += self.input_cells[i] * self.input_weights[i][j]self.hidden_cells[j] = sigmoid(total)for k in range(self.output_n):total = 0.0for j in range(self.hidden_n):total += self.hidden_cells[j] * self.output_weights[j][k]self.output_cells[k] = sigmoid(total)return self.output_cells[:]#浅拷贝def back_propagate(self,case,label,learn):self.predict(case)#计算输出层的误差output_deltas = [0.0] * self.output_nfor k in range(self.output_n):error = label[k] - self.output_cells[k]output_deltas[k] = sigmod_derivate(self.output_cells[k]) * error#误差项#计算隐藏层的误差hidden_deltas = [0.0] * self.hidden_nfor j in range(self.hidden_n):error = 0.0for k in range(self.output_n):error += output_deltas[k] * self.output_weights[j][k]hidden_deltas[j] = sigmod_derivate(self.hidden_cells[j]) * error#更新输出层权重for j in range(self.hidden_n):for k in range(self.output_n):self.output_weights[j][k] += learn * output_deltas[k] * self.hidden_cells[j]#更新隐藏层权重for i in range(self.input_n):for j in range(self.hidden_n):self.input_weights[i][j] += learn * hidden_deltas[j] * self.input_cells[i]error = 0for o in range(len(label)):error += 0.5 * (label[o] - self.output_cells[o]) ** 2return errordef train(self,cases,labels,limit = 100,learn = 0.05):for i in range(limit):error = 0for i in range(len(cases)):label = labels[i]case = cases[i]error += self.back_propagate(case, label, learn)passdef test(self):cases = [[0, 0],[0, 1],[1, 0],[1, 1],]labels = [[0], [1], [1], [0]]self.setup(2, 5, 1)self.train(cases, labels, 1000000, 0.05)for case in cases:print(self.predict(case))
if __name__ == '__main__':nn = BPNeuralNetwork()nn.test()

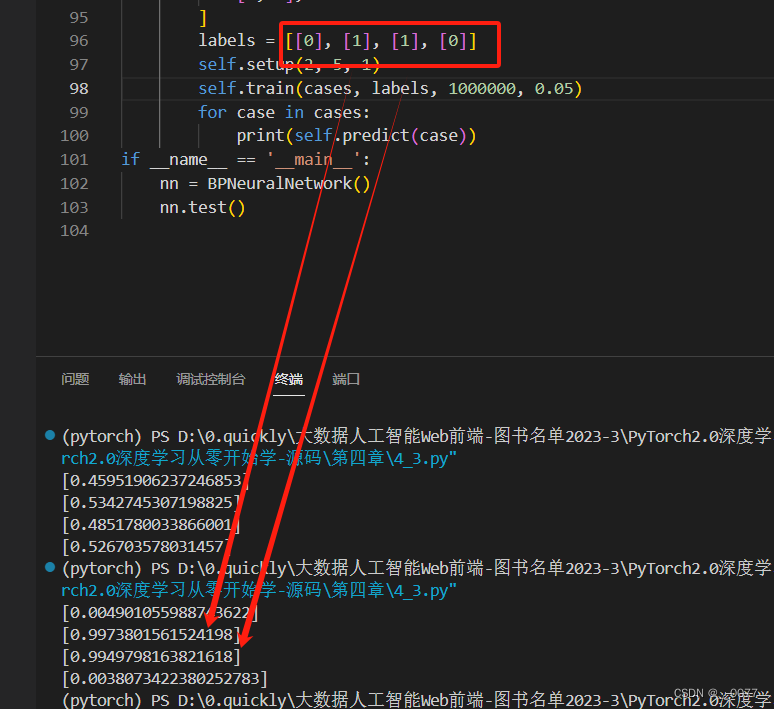
运行结果：原有的训练结果不太理想，直接把训练次数后面加了2个0,效果好多了~

这篇关于【自学记录】【Pytorch2.0深度学习从零开始学 王晓华】第四章 深度学习的理论基础的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---