基于DCT和扩频的音频水印嵌入提取算法matlab仿真

本文主要是介绍基于DCT和扩频的音频水印嵌入提取算法matlab仿真，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

1.算法运行效果图预览

2.算法运行软件版本

3.部分核心程序

4.算法理论概述

5.算法完整程序工程

1.算法运行效果图预览

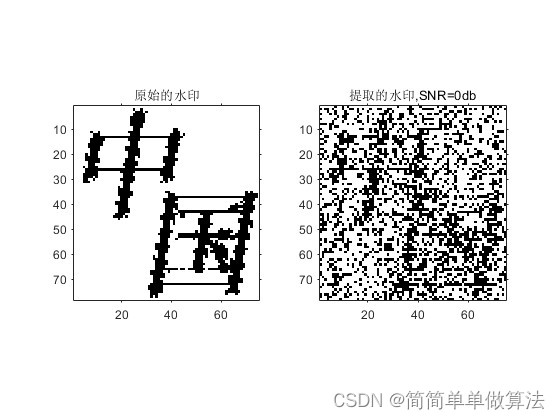
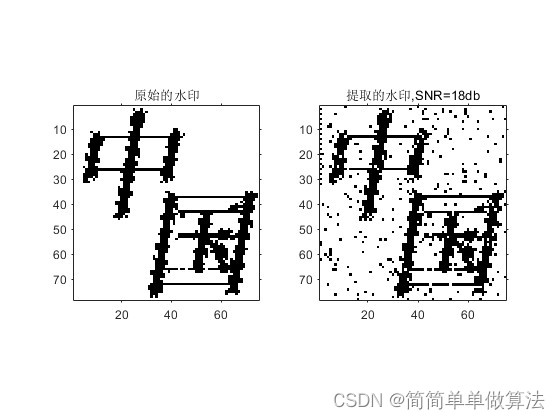
2.算法运行软件版本

matlab2022a

3.部分核心程序

.........................................................................
N = 10; %嵌入一个水印信息需要的音频数据为N
length = n*10;
i = 1 : length;% 将原始音频信号分解为Ae和Ar两部分 
j = [1];
Ae = A(i,j);% 取矩阵A的l到length行构建矩阵Ae
i = length+1 : L;
Ar = A(i,j);% 取矩阵A的length到L行第一列构建矩阵Ark = 1;
B = cell(n,1);% 建立M1 x M2行l列的元胞
th = n*N;
while ( k < th )i = k : k+9;m = (k+9)/10;B{m,1} = Ae(i,j);k = k+10;
end
D = cell(n,1);
for i = 1 : nD{i,1} = dct(B{i,1});%DCT变化
endE = cell(n,1);% 建立元胞E，储存嵌有水印信号的中频系数
E = D;
for i = 1 : nE{i,1}(3) = (D{i,1}(3))*(1+2*S(i)); % 将扩频了的水印信息S嵌入音频中
endF = cell(n,1);
for i = 1 : nF{i,1} = idct(E{i,1});% 将元胞E中离散余弦反变换了的元素存入元胞F中
endG = F{1,1};
for i = 2 : nG=[G; F{i,1}];
endG =[G; Ar];% 将元胞G和矩阵Ar合并创建一维矩阵G
audiowrite('after1.wav',G,fs);
subplot(212); plot(G); 
axis([0 350000 -2 2]);
011_001m

4.算法理论概述

音频水印作为一种数字版权保护手段，能够在不影响音频质量的前提下，将特定信息（如身份标识、版权信息等）隐秘地嵌入到音频信号中。DCT因其良好的能量集中特性与离散傅里叶变换（Discrete Fourier Transform, DFT）相比在实数域运算的优势，常被用于音频信号的变换域处理。而扩频技术通过将水印信号扩展至较宽的频率范围，增强了水印的隐蔽性和抗攻击能力。本文将详细介绍这两种技术如何结合，实现音频水印的高效、安全嵌入与提取。

DCT是一种将离散信号从时域转换到频域的线性变换，尤其适用于处理具有相关性的实数信号。对于长度为N的一维音频信号x[n],n=0,1,…,N−1，其DCT变换定义为：

DCT变换后的系数X[k]反映了原始信号在不同频率分量上的能量分布，其中低频系数通常包含信号的主要信息，高频系数则包含细节和噪声。在音频水印嵌入过程中，选择合适的频带进行水印嵌入可以兼顾隐蔽性和鲁棒性。

扩频（Spread Spectrum, SS）是一种通过将窄带信号扩展至较宽的频带进行传输的技术，旨在提高通信系统的抗干扰和保密性能。在音频水印中，扩频技术用于将水印信号“隐藏”在音频信号的多个频率分量中，降低单一分量对水印信息的影响，提高水印的隐蔽性和抗攻击能力。

结合离散余弦变换（DCT）与扩频技术的音频水印嵌入与提取算法，充分利用了DCT在音频信号处理中的优势，以及扩频技术在提高水印隐蔽性和鲁棒性方面的特性。通过详细阐述算法原理、数学表达与实施步骤，本文展示了该方法的专业性和有效性。未来研究可进一步探索自适应嵌入策略、鲁棒性增强技术、以及针对特定攻击的防御机制，以提升音频水印系统的实用性和安全性。