本文主要是介绍Lesson 8 Batch Normalization,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
听课(李宏毅老师的)笔记,方便梳理框架,以作复习之用。本节课主要讲了batch normalization是什么,为什么要用batch normalization,是用来解决什么问题的,以及batch normalization在测试和训练上不同的计算方法
1. changing landscape
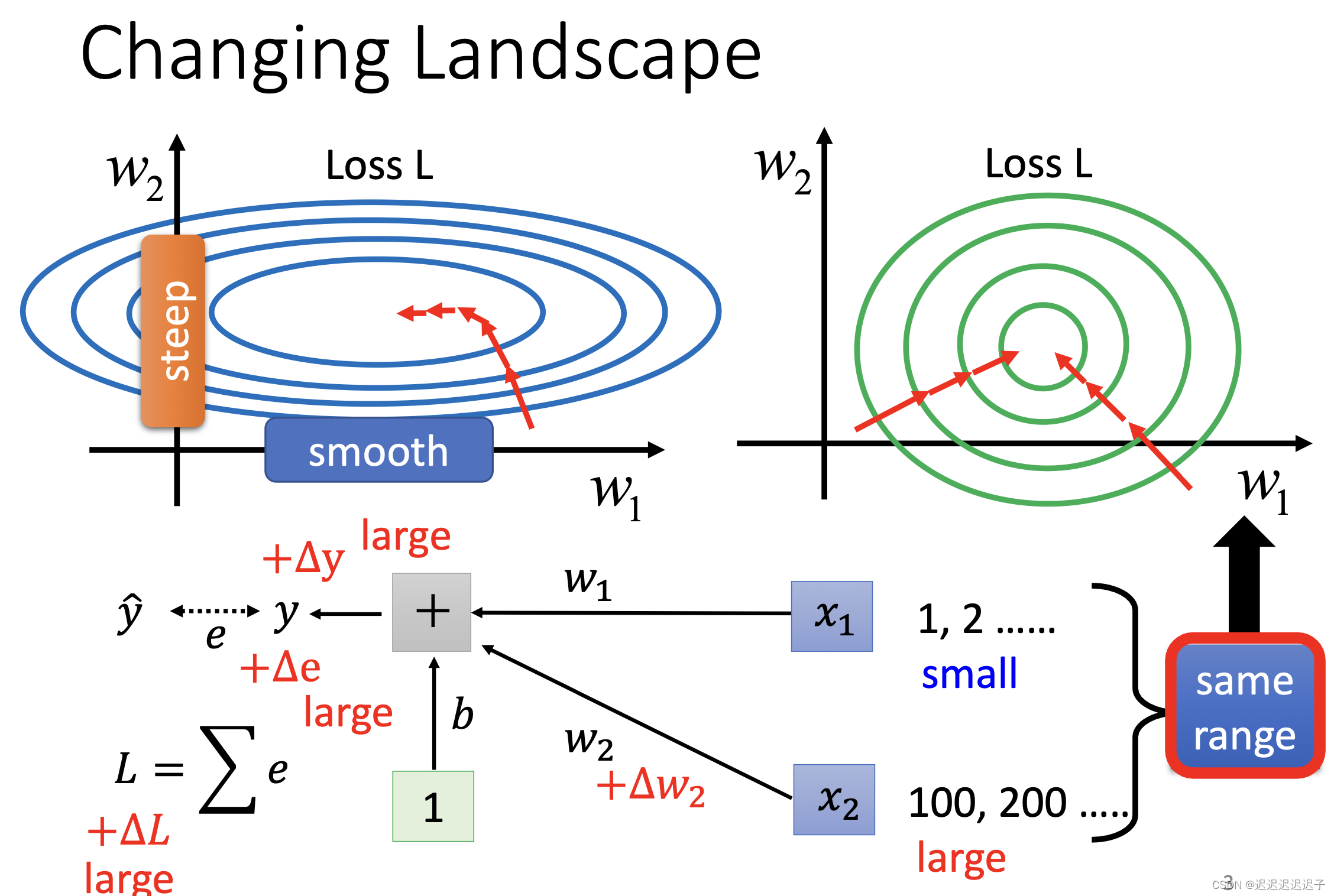
陡峭的error surface难train,因为这样的error surface对于参数的变化非常敏感,即使是微小的参数变化都可能导致错误值剧烈变化,不利于找到全局最优。
那么想让error surface变得平坦应该怎么做?
我们可以看下图,考虑两种输入X1=[1,2,3]和X2=[100,200,300],不难看出,由于X1引起的△L和由于X2引起的△L是不一样的,第二个△L明显偏大,这就造成了error surface的陡峭。如果我们将输入的X都变成一样的range,那么error surface也会变得各维度相似的平坦
2. feature normalization
输入的特征中,将同一维度的x加起来,算出平均值和σ
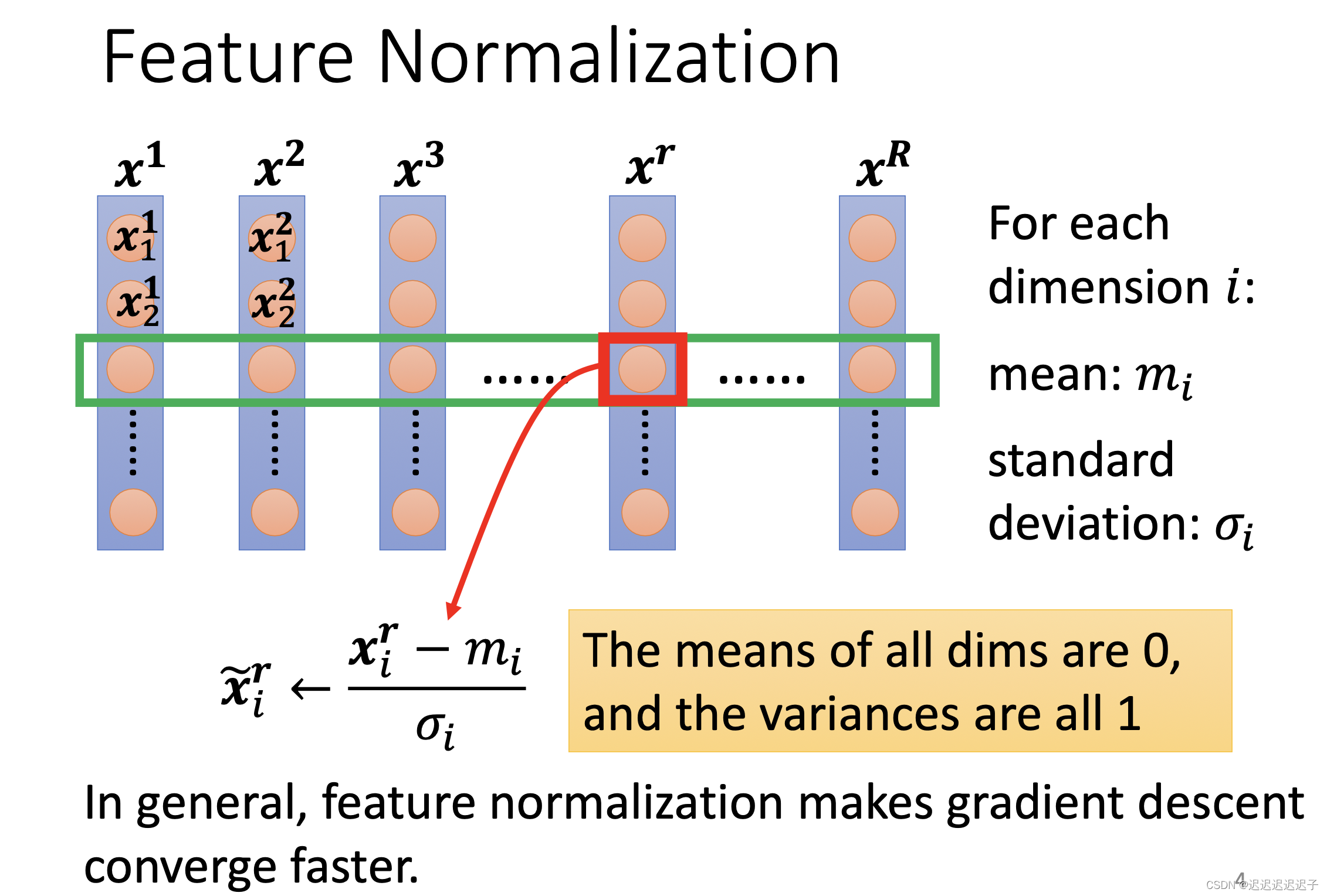
在经过第一层与W相乘后
得到的输出其实也可以看成下一层的输入,所以也可以做batch normalization。
又有一个问题出现了:是在active function之前做normalization 还是之后呢?
其实在实际操作中影响不大。所以无所谓。

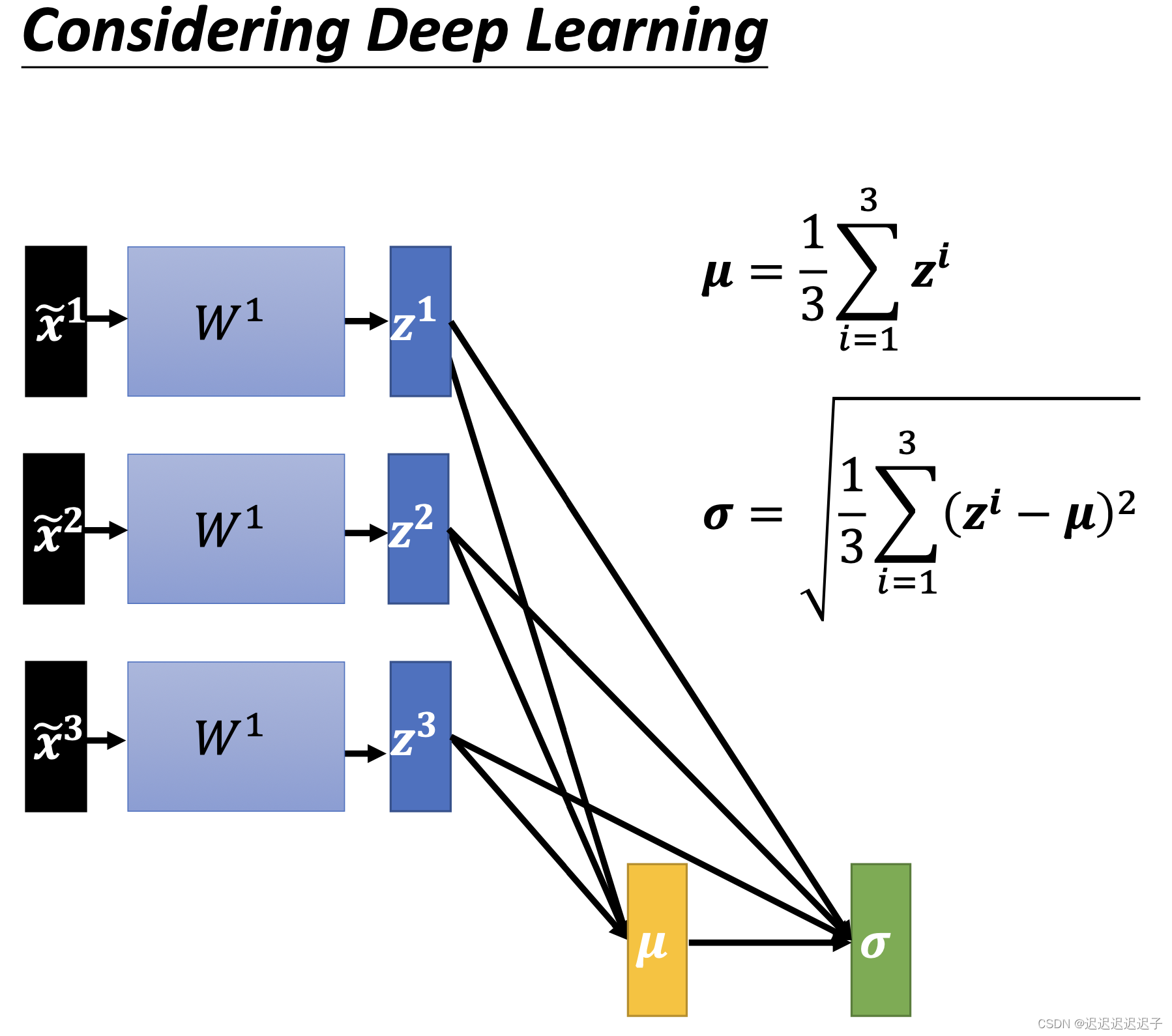
如果z1改变,那么下图右侧所有的变量都要改,对于一个大网络来说,需要改变的data就非常多。
所以我们一般在batch内做normalization,这样计算量就不会那么大。这也是为什么叫 batch normalization。
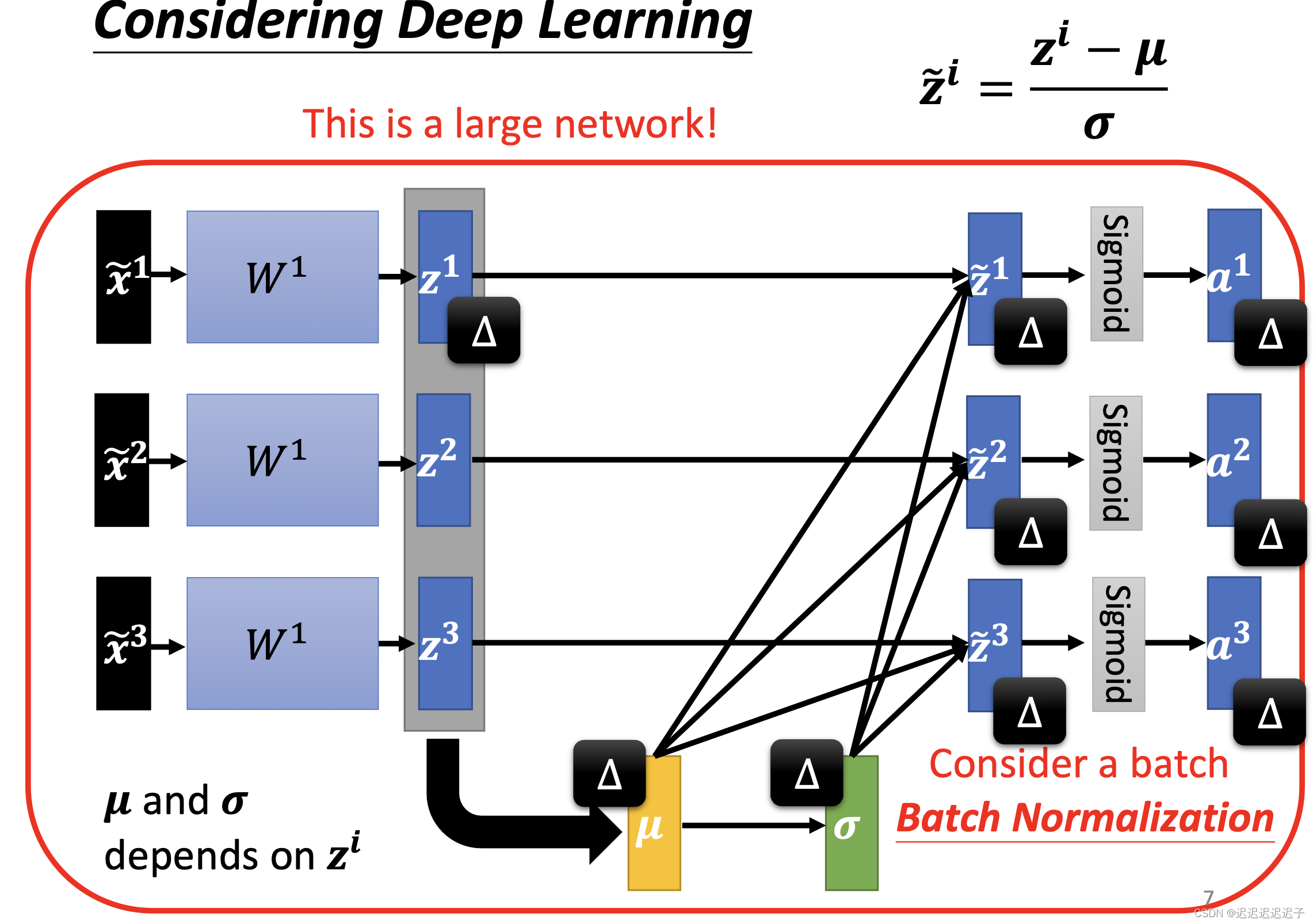
3. batch normalization
3.1 训练
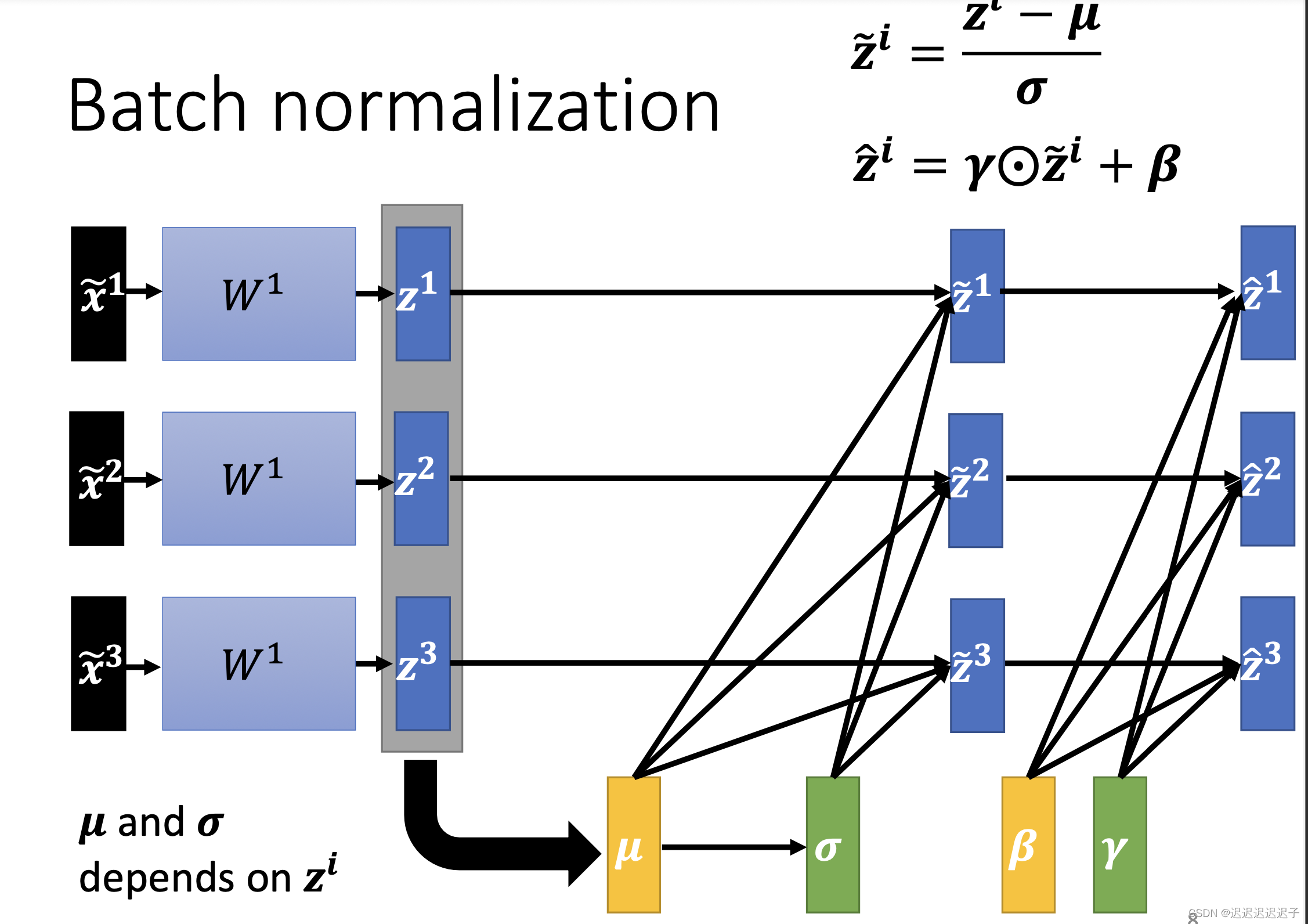
β和γ又是什么?
因为在z1,z2经过batch normalization后的平均数是0(因为本人不知道那个带~的字母怎么打哈哈),所以可能给network带来一些限制,这种限制可能会有负面影响。
那又有疑问了,*γ又+β,不是又不符合normalization了吗?本来是想要normalization的,现在又不是了,感觉不是很有病吗?实际上初始时,γ是one-vector,就全是1,而β是zero-vector,全是0,所以最开始还是符合normalization的,等找到比较好的error surface后,才把β和γ慢慢加进去。
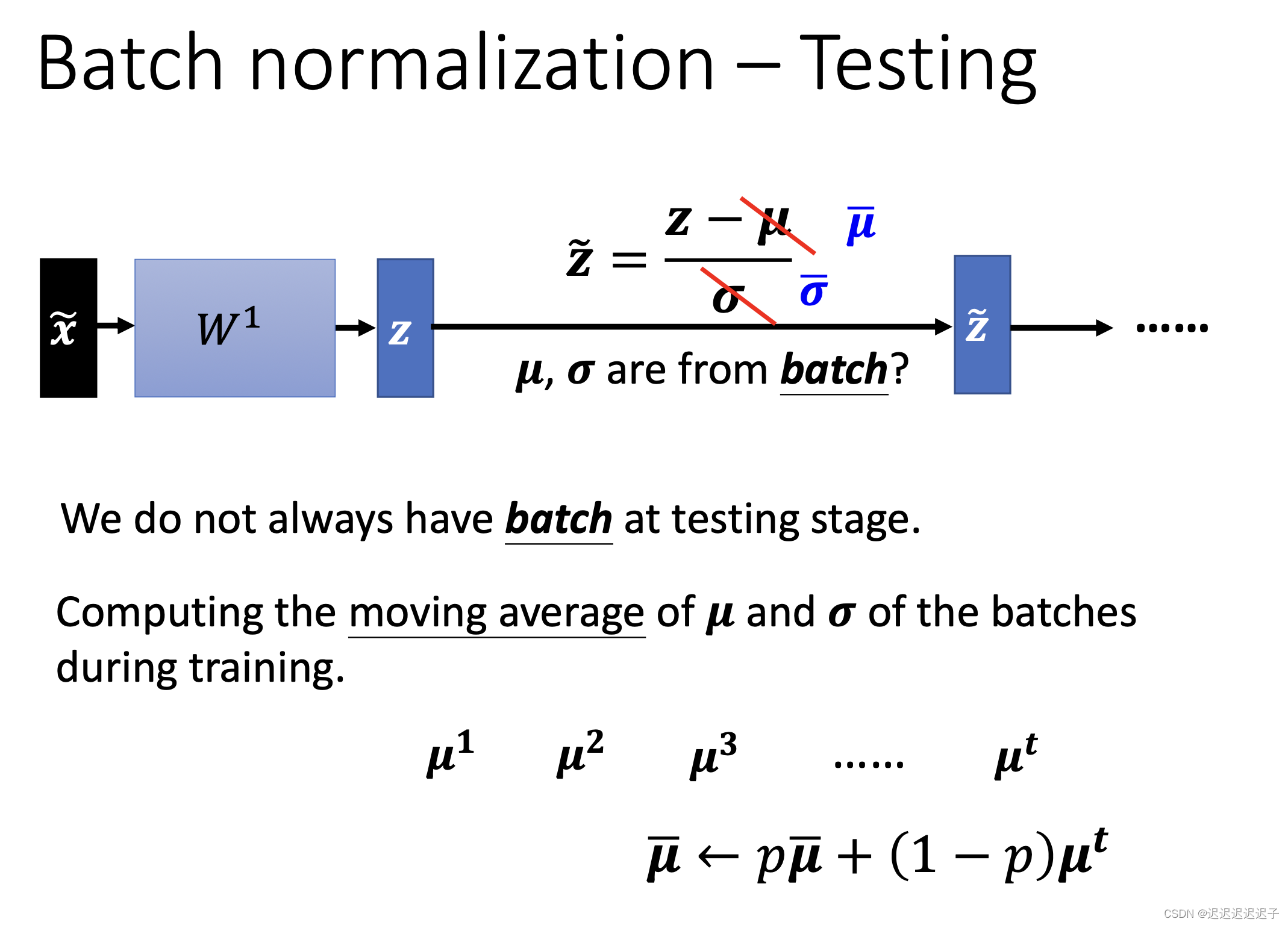
3.2 测试
假如一个batch是64,如果是线上服务,不可能等到攒够64笔资料才做normalization,所以在testing的时候用的是moving average。moving average计算方式如下。
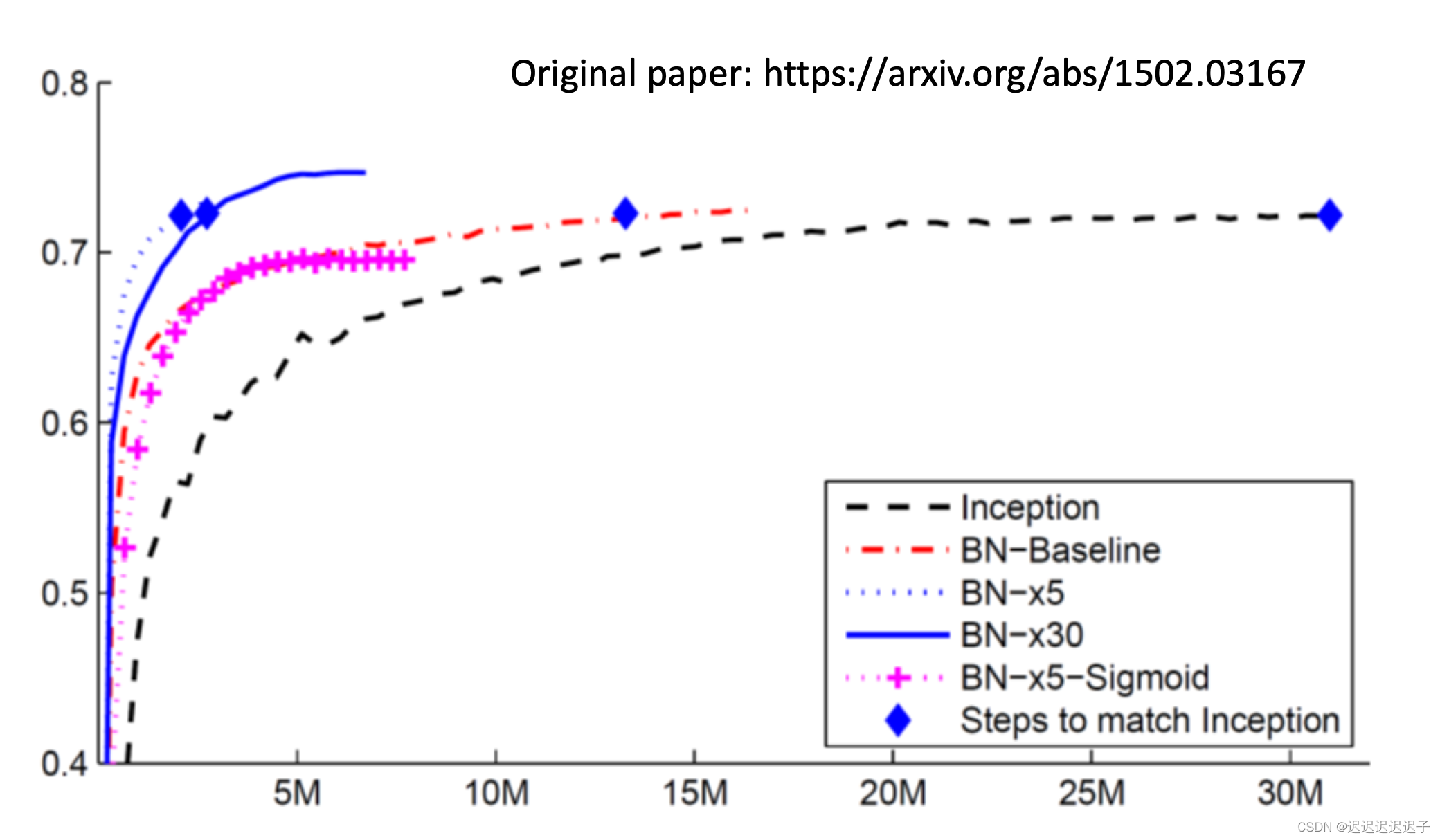
在各模型测试结果如下。可以看出,使用了normalization训练会更快达到较高的准确度。
4. internal covariate shift
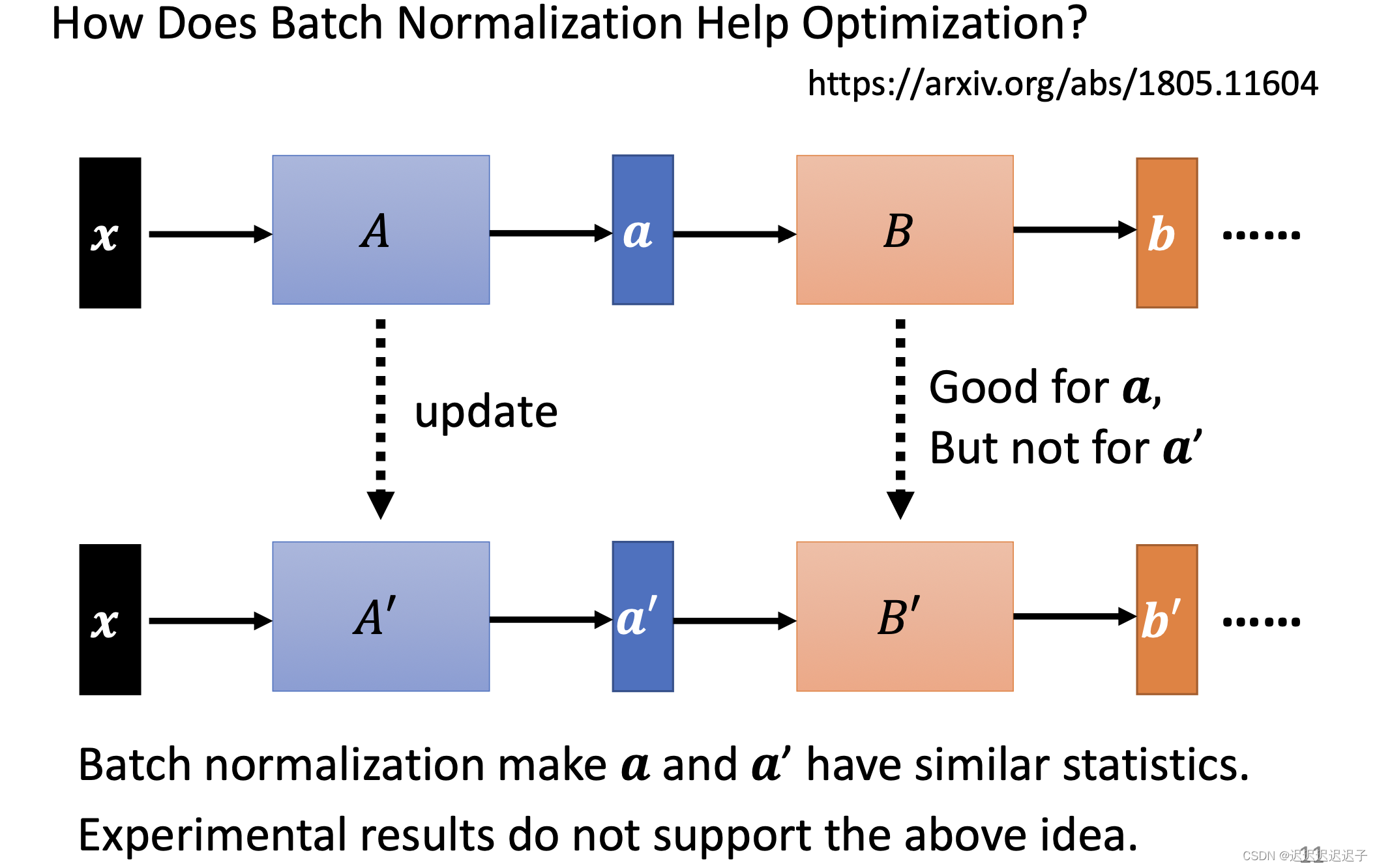
gradient是根据a算出来的,适合用在a上不适合用在a’上。就说让a和a’有相同的分布比较好。但是有论文叫“how does batch normalization help optimization”打脸了这个观点,他认为a和a’的分布相不相同都不影响训练

这篇关于Lesson 8 Batch Normalization的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!