C++王牌结构hash：哈希表开散列(哈希桶)的实现与应用

本文主要是介绍C++王牌结构hash：哈希表开散列(哈希桶)的实现与应用，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

目录

一、开散列的概念

1.1开散列与闭散列比较

二、开散列/哈希桶的实现

2.1开散列实现

哈希函数的模板构造

哈希表节点构造

开散列增容

插入数据

2.2代码实现

---

一、开散列的概念

开散列法又叫链地址法(开链法)，首先对关键码集合用散列函数计算散列地址，具有相同地址的关键码归于同一子集合，每一个子集合称为一个桶，各个桶中的元素通过一个单链表链接起来，各链表的头结点存储在哈希表中。

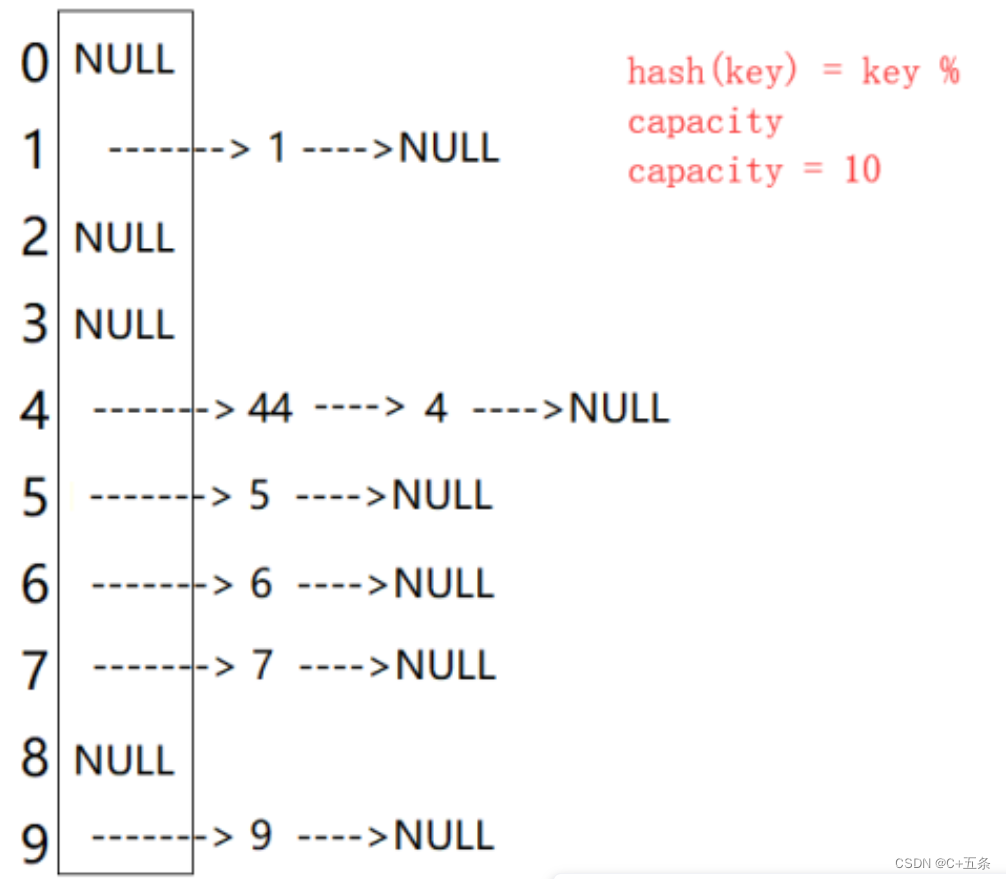
从上图可以看出，开散列中每个桶中放的都是发生哈希冲突的元素。

1.1开散列与闭散列比较

应用链地址法处理溢出，需要增设链接指针，似乎增加了存储开销。事实上： 由于开地址法必须保持大量的空闲空间以确保搜索效率，如二次探查法要求装载因子a <= 0.7，而表项所占空间又比指针大的多，所以使用链地址法反而比开地址法节省存储空间。

二、开散列/哈希桶的实现

2.1开散列实现

哈希函数的模板构造

当数据类型不是整数时，我们需要通过哈希函数将其转换为一个size_t类型的无符号整形然后%上哈希表的容量得出一个映射值，所以需要针对不同的数据类型，来构造不同的Hashfunc来将其转换为size_t类型，这时就要用到模板特化来处理数据，尤其是字符串类型。

哈希表节点构造

同时针对set和map的不同，我们需要将hash桶的模板可以满足两种不同类型的调用，所以在参数上也要设置两个参数，如果是set传参，就让两个参数都是K，如果是map传参，第一个参数是K，第二个参数则是pair<K,V>，而在构造哈希表的node时，不管是set还是map都只需要传第二个参数过去，而hashnode也只需要用一个template<class T>来进行接收就好，然后构造初始化出T _data和一个T* _next的指针来指向桶中下一个节点。

那为什么在传参时不直接只设置一个参数呢？因为在调用find时，需要传一个值进去查找，如果是set则直接查找，如果是map则需要取出hashnode中的first与之进行比较，所以必须设置两个模板参数。

开散列增容

桶的个数是一定的，随着元素的不断插入，每个桶中元素的个数不断增多，极端情况下，可能会导致一个桶中链表节点非常多，会影响的哈希表的性能，因此在一定条件下需要对哈希表进行增容，那该条件怎么确认呢？开散列最好的情况是：每个哈希桶中刚好挂一个节点，再继续插入元素时，每一次都会发生哈希冲突，因此，在元素个数刚好等于桶的个数时，可以给哈希表增容。

插入数据

因为开散列每个位置都是一串单链表，所以在插入节点时，直接选择头插即可，头插的消耗和速度都是最小的。

2.2代码实现

#pragma once
#include<iostream>
using namespace std;
#include<vector>
#include<string>template<class K>
struct HashFunc
{size_t operator()(const K& key){return (size_t)key;}
};// 特化
template<>
struct HashFunc<string>
{size_t operator()(const string& s){size_t hash = 0;for (auto e : s){hash += e;hash *= 131;}return hash;}
};
namespace hash_bucket
{//如果是unordered_set的话T=K//如果是unordered_map的话T=pair<K,V>template<class T>struct HashNode{HashNode<T>* _next;T _data;HashNode(const T& data):_next(nullptr),_data(data){}};// 前置声明,因为编译器编译时会向上进行查找，而iterator要去调用哈希表，所以需要提前进行前置声明template<class K, class T, class Keyoft, class Hash >class HashTable;//迭代器实现template<class K, class T, class Keyoft, class Hash >struct __HTIterator{typedef HashNode<T> Node;typedef HashTable<K, T, Keyoft, Hash> HT;typedef __HTIterator<K, T, Keyoft, Hash> Self;Node* _node;HT* _ht;__HTIterator(Node* node,HT* ht):_node(node),_ht(ht){}T& operator*(){return _node->_data;}Self& operator++(){//如果当前桶内还有节点if (_node->_next){_node = _node->_next;}else{//当前桶找完，就去找下一个桶Keyoft kot;Hash hs;size_t hashi = hs(kot(_node->_data)) % _ht->_tables.size();hashi++;while (hashi < _ht->_tables.size()){if (_ht->_tables[hashi]){_node = _ht->_tables[hashi];break;}hashi++;}//如果后面没有桶if (hashi == _ht->_tables.size()){_node = nullptr;}}return *this;}bool operator!=(const Self& s){return _node != s._node;}};//哈希桶搭建template<class K, class T,class Keyoft,class Hash>class HashTable{template<class K, class T, class KeyOfT, class Hash>friend struct __HTIterator;typedef HashNode<T> Node;public:typedef __HTIterator< K, T, Keyoft, Hash> iterator;HashTable(){_tables.resize(10, nullptr);_n = 0;}~HashTable(){for (size_t i = 0; i < _tables.size(); i++){Node* cur = _tables[i];while (cur){Node* next = cur->_next;delete cur;cur = next;}_tables[i] = nullptr;}}iterator begin(){for (size_t i = 0; i < _tables.size(); i++){// 找到第一个桶的第一个节点if (_tables[i]){return iterator(_tables[i], this);}}return end();}iterator end(){return iterator(nullptr, this);}//插入节点bool insert(const T& data){Keyoft kot;if (Find(kot(data)))return false;Hash hs;//负载因子到1就扩容if (_n == _tables.size()){vector<Node*> newtables(_tables.size() * 2,nullptr);for (size_t i = 0; i < _tables.size(); i++){Node* cur = _tables[i];while (cur){Node* next = cur->_next;//头插到新表size_t hashi = hs(kot(cur->_data)) % newtables.size();newtables[hashi] = cur;cur = next;}_tables[i] = nullptr;}_tables.swap(newtables);}size_t hashi = hs(kot(data)) % _tables.size();Node* newnode = new Node(data);//头插newnode->_next = _tables[hashi];_tables[hashi] = newnode;++_n;return true;}//查找Node* Find(const K& key){Hash hs;Keyoft kot;size_t hashi = hs(key) % _tables.size();Node* prev = nullptr;Node* cur = _tables[hashi];while (cur){if (kot(cur->_data) == key)return cur;cur = cur->_next;}return nullptr;}Node* Erase(const K& key){Hash hs;Keyoft kot;size_t hashi = hs(key) % _tables.size();Node* prev = nullptr;Node* cur = _tables[hashi];while (cur){if (kot(cur->_data) == key){if (prev == nullptr){_tables[hashi] = cur->next;}else{prev->_next = cur->_next;}}prev = cur;cur = cur->_next;}return false;}private:vector<Node*> _tables;//指针数组size_t _n;};
}

这篇关于C++王牌结构hash：哈希表开散列(哈希桶)的实现与应用的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---