本文主要是介绍代码随想录算法训练营第二十四天| 理论基础,77. 组合,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
题目与题解
参考资料:回溯法理论基础
带你学透回溯算法(理论篇)| 回溯法精讲!_哔哩哔哩_bilibili
77. 组合
题目链接:77. 组合
代码随想录题解:77. 组合
视频讲解:带你学透回溯算法-组合问题(对应力扣题目:77.组合)| 回溯法精讲!_哔哩哔哩_bilibili
带你学透回溯算法-组合问题的剪枝操作(对应力扣题目:77.组合)| 回溯法精讲!_哔哩哔哩_bilibili
解题思路:
回溯法的题目之前很少做,对于这一道题,手写穷举是很好写的,如果只有两个数的组合,求两层for循环即可,但是当k很大时,就比较难直接暴力写for循环了。
这一题主要是初步体验一下回溯法的流程,所以直接看答案了。
看完代码随想录之后的想法
回溯法的要点:
- 回溯法解决的问题都可以抽象为树形结构(N叉树),树的每深入一层相当于递归操作,而在每层上的操作一般都是循环处理。
- 每次搜索到了叶子节点,我们就找到了一个结果,因此找到叶子节点一般是终止条件。
- 为了提高穷举效率,可以针对N叉树做剪枝操作,避免不必要的递归和循环。
回溯法一般的函数体为:
void backtracking(参数) {if (终止条件) {存放结果;return;}for (选择:本层集合中元素(树中节点孩子的数量就是集合的大小)) {处理节点;backtracking(路径,选择列表); // 递归回溯,撤销处理结果}
}对于这道题,其N叉树为
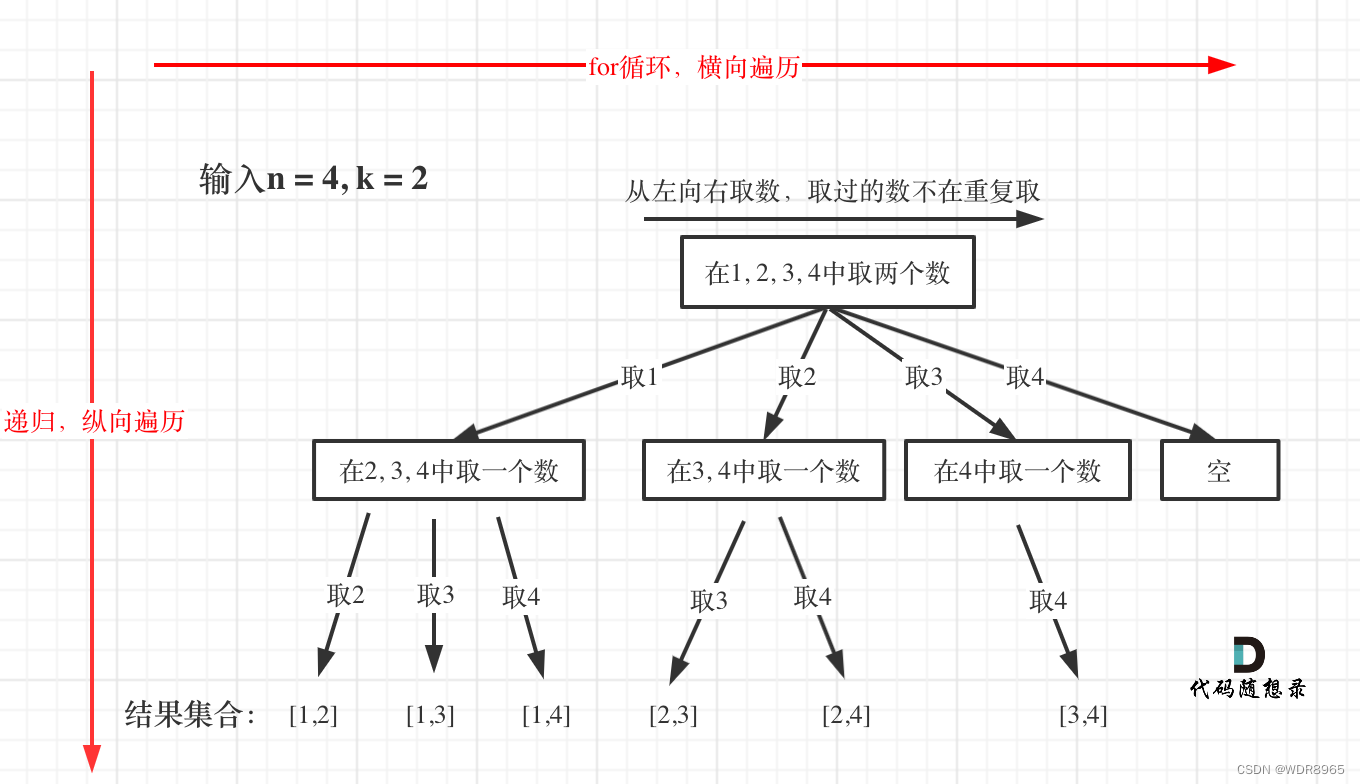
每次循环的起始值startIndex就是取1,2,3...的操作,而终止条件就是当前循环的一个符合条件的list已经满了,达到了叶子节点,将结果塞入result的list后,还需要将list最末尾的节点弹出,方便下一次操作。
class Solution {List<List<Integer>> result= new ArrayList<>();LinkedList<Integer> path = new LinkedList<>();public List<List<Integer>> combine(int n, int k) {backtracking(n,k,1);return result;}public void backtracking(int n,int k,int startIndex){if (path.size() == k){result.add(new ArrayList<>(path));return;}for (int i =startIndex;i<=n;i++){path.add(i);backtracking(n,k,i+1);path.removeLast();}}
}当然,考虑到如果从startIndex到n的元素数目不足k,那么就算循环结束这个path也不会被使用,浪费了时间,可以提前剪枝,因此循环中i的上限设置为n - (k - path.size()) + 1 ,注意path.size()是小于等于k的。这样就完成了剪枝。
class Solution {List<List<Integer>> result = new ArrayList<>();LinkedList<Integer> path = new LinkedList<>();public List<List<Integer>> combine(int n, int k) {combineHelper(n, k, 1);return result;}/*** 每次从集合中选取元素,可选择的范围随着选择的进行而收缩,调整可选择的范围,就是要靠startIndex* @param startIndex 用来记录本层递归的中,集合从哪里开始遍历(集合就是[1,...,n] )。*/private void combineHelper(int n, int k, int startIndex){//终止条件if (path.size() == k){result.add(new ArrayList<>(path));return;}for (int i = startIndex; i <= n - (k - path.size()) + 1; i++){path.add(i);combineHelper(n, k, i + 1);path.removeLast();}}
}遇到的困难
我一开始按照答案的思路抄写,但是没有用linkedlist作为存储path的变量而是用了list,在result.add的时候直接插入了path,结果每次输出的结果都是全空的。debug的时候很奇怪,插入result的一瞬间结果是对的,到下一层遍历的时候result里面的元素竟然减少了。就很奇怪。
查阅了以后才知道,java中的list如果直接被加入list.add(list),传入的是list的引用,而非拷贝。所以即使当时把path加入了result,随着后面回溯时要弹出元素,被引用加入result的path自然也会随之改变。
正确的做法是每次拷贝一份新的path,即不用result.add(path)而是result.add(new ArrayList<>(path)),这样path就算有任何变化,也不会影响这一份拷贝。
今日收获
初步学习了一下回溯法的思路,并且用组合这道题为例理解了一下回溯法,还学习了java中list的实际传递方式。不过还是有点云里雾里的,需要再做一点题来熟悉。
这篇关于代码随想录算法训练营第二十四天| 理论基础,77. 组合的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





