算法---动态规划练习-7（按摩师）【类似打家劫舍】

本文主要是介绍算法---动态规划练习-7（按摩师）【类似打家劫舍】，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

1. 题目解析

题目地址：点这里

2. 讲解算法原理

---

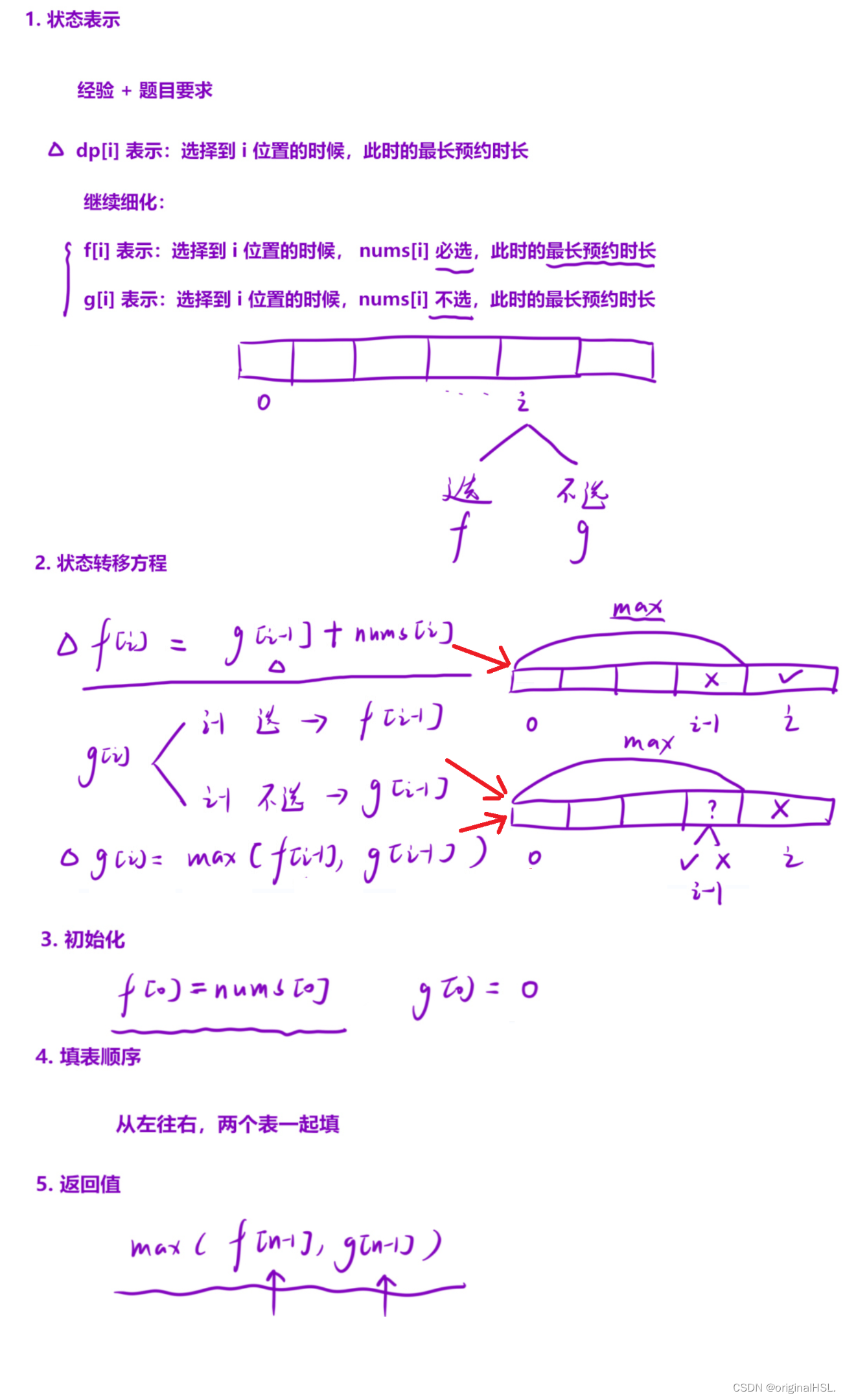
1. 首先，给定一个整数数组 nums，其中 nums[i] 表示第 i 天的预约时间长度。

2. 定义两个辅助数组 f 和 g，长度都为 n（n 是数组 nums 的长度）。

   • 数组 f 表示在第 i 天选择预约时的最大总时长。
   • 数组 g 表示在第 i 天选择不预约时的最大总时长。

3. 初始化数组 f 和 g 的第一个元素：

   • f[0] = nums[0]，表示第一天选择预约，总时长为第一天的预约时长。
   • g[0] = 0，表示第一天选择不预约，总时长为0。

4. 从第二天开始，从左到右遍历整个数组 nums，计算每一天的最大总时长：

   • 对于第 i 天，如果选择预约，则总时长为前一天选择不预约的最大总时长 g[i-1] 加上第 i 天的预约时长 nums[i]，即 f[i] = g[i-1] + nums[i]。
   • 对于第 i 天，如果选择不预约，则总时长为前一天选择预约和不预约的最大总时长中的较大值，即 g[i] = max(f[i-1], g[i-1])。

5. 最后，返回最后一天选择预约和不预约的最大总时长的较大值，即 max(f[n-1], g[n-1])，其中 n 是数组 nums 的长度。

---

3. 编写代码

class Solution {
public:int massage(vector<int>& nums) {int n=nums.size();//处理细节if(n==0) return 0;vector<int> f(n);   vector<int> g(n); f[0]=nums[0],g[0]=0;for(int i=1;i<n;i++){f[i]=g[i-1]+nums[i];g[i]=max(f[i-1],g[i-1]);} return max(f[n-1],g[n-1]);}
};

这篇关于算法---动态规划练习-7（按摩师）【类似打家劫舍】的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---