本文主要是介绍代码随想录算法训练营第二十二天|235. 二叉搜索树的最近公共祖先,701.二叉搜索树中的插入操作,450.删除二叉搜索树中的节点,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
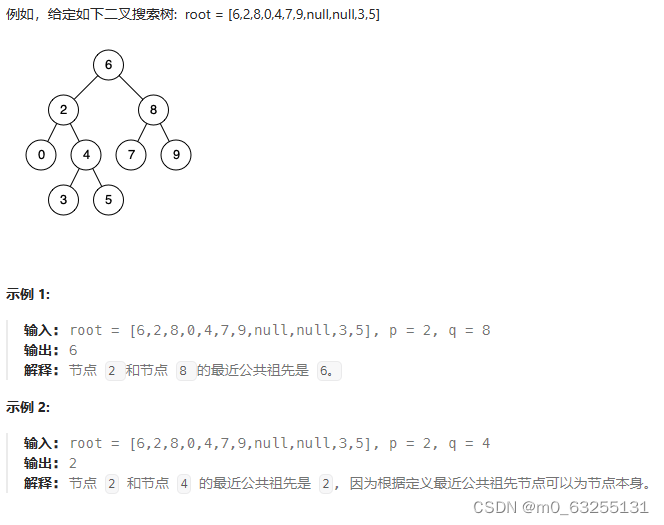
题目:235. 二叉搜索树的最近公共祖先
给定一个二叉搜索树,找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为:“对于有根树 T 的两个结点 p、q,最近公共祖先表示为一个结点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。”
题目链接/文章讲解:https://programmercarl.com/0235.%E4%BA%8C%E5%8F%89%E6%90%9C%E7%B4%A2%E6%A0%91%E7%9A%84%E6%9C%80%E8%BF%91%E5%85%AC%E5%85%B1%E7%A5%96%E5%85%88.html
视频讲解:https://www.bilibili.com/video/BV1Zt4y1F7ww
思路
1、本题是二叉搜索树的最近公共祖先,与236. 二叉树的最近公共祖先这一题可以采用相同的解法。
2、利用二叉搜索树有序的性质:二叉搜索树的左子树节点的值都小于根节点的值,右子树节点的值都大于根节点的值。
如果p、q的值都大于根节点的值,p、q都在右子树,就去右子树里面搜索;如果都小于根节点的值,都在左子树;一个大于一个小于,那就一个在左子树一个在右子树。
当搜索到最深处的时候,p和q相对于某个节点一定就是一左一右,因为每个节点的值都是唯一的,且p和q不会是同一个节点(题目的要求)。
解题
1、和236题一样的代码
class Solution {
public:TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {if (root == NULL || root == p || root == q)return root;TreeNode* left = lowestCommonAncestor(root->left, p, q);TreeNode* right = lowestCommonAncestor(root->right, p, q);if (left && right)return root;else if (!left && right)return right;else if (left && !right)return left;elsereturn NULL;}
};
2、利用有序的性质
class Solution {
public:TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {if (root->val > p->val && root->val > q->val) {TreeNode* left = lowestCommonAncestor(root->left, p, q);return left;} else if (root->val < p->val && root->val < q->val) {TreeNode* right = lowestCommonAncestor(root->right, p, q);return right;} elsereturn root;}
};
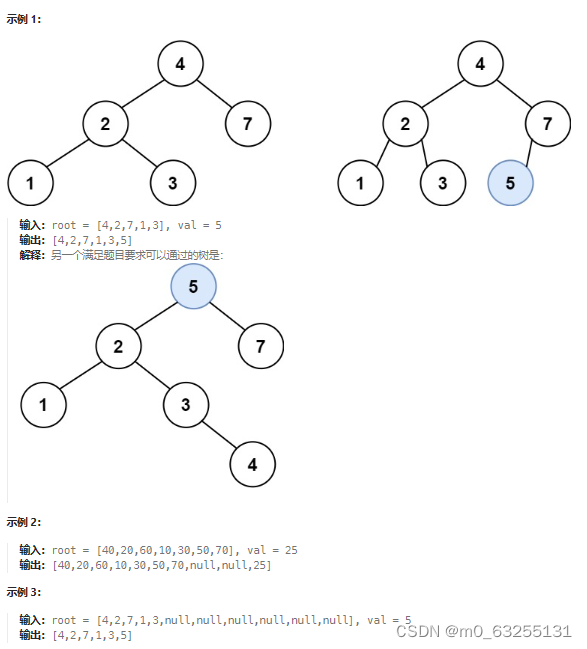
题目: 701.二叉搜索树中的插入操作
给定二叉搜索树(BST)的根节点 root 和要插入树中的值 value ,将值插入二叉搜索树。 返回插入后二叉搜索树的根节点。输入数据保证,新值和原始二叉搜索树中的任意节点值都不同。
注意,可能存在多种有效的插入方式,只要树在插入后仍保持为二叉搜索树即可。 你可以返回任意有效的结果。
题目链接/文章讲解:https://programmercarl.com/0701.%E4%BA%8C%E5%8F%89%E6%90%9C%E7%B4%A2%E6%A0%91%E4%B8%AD%E7%9A%84%E6%8F%92%E5%85%A5%E6%93%8D%E4%BD%9C.html
视频讲解:https://www.bilibili.com/video/BV1Et4y1c78Y
思路
遍历二叉树,找到空节点插入即可。
解题
class Solution {
public:TreeNode* insertIntoBST(TreeNode* root, int val) {if (root == NULL) {TreeNode* node = new TreeNode(val);return node;}if (root->val > val) root->left = insertIntoBST(root->left, val);if (root->val < val) root->right = insertIntoBST(root->right, val);return root;}
};
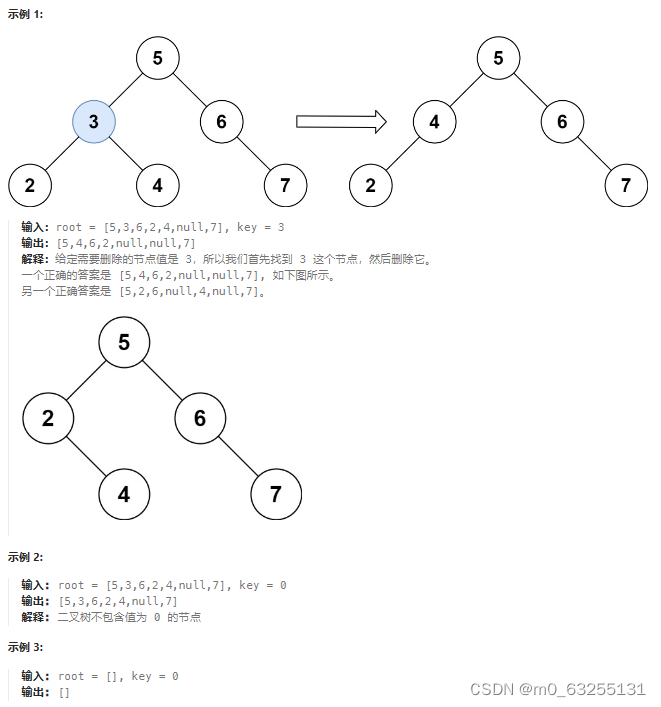
题目:450.删除二叉搜索树中的节点
给定一个二叉搜索树的根节点 root 和一个值 key,删除二叉搜索树中的 key 对应的节点,并保证二叉搜索树的性质不变。返回二叉搜索树(有可能被更新)的根节点的引用。
一般来说,删除节点可分为两个步骤:1、首先找到需要删除的节点;
2、如果找到了,删除它。
题目链接/文章讲解:https://programmercarl.com/0450.%E5%88%A0%E9%99%A4%E4%BA%8C%E5%8F%89%E6%90%9C%E7%B4%A2%E6%A0%91%E4%B8%AD%E7%9A%84%E8%8A%82%E7%82%B9.html
视频讲解:https://www.bilibili.com/video/BV1tP41177us
思路
我们要删除一个节点,首先要找到这个节点。
寻找这个节点,会有两种情况:
1.没到了;2.没找到
对于1,没找到,说明树不会被修改,将原来的树原封不动返回。
对于2,找到了,肯定返回的是最终删除了指定元素的树。
对于找到的节点,即当前的节点的val==key,也分为了下面四种情况:
1、当前节点左右子树都为空:直接删除这个结点,不用改变结构;
2、当前节点左子树不为空,右子树为空:用左子树替代当前结点;
3、当前结点左子树为空,右子树不为空:用右子树替代当前结点;
4、当前结点左右子树都不为空:
先将当前节点左子树,放在当前节点右子树的最左侧孩子的左子树位置上
用当前结点右子树代替当前结点
对于第4中情况,为什么要这么做?
1)由于这是二叉搜索树,当前结点左子树上所有元素都是小于当前结点右子树上最小元素的;
2)当前结点右子树上最小元素就是当前结点右子树上最左侧的元素;
3)所以,将左子树放在右子树最左侧结点的左子树位置是没有问题的。
当前节点的val > key:说明目标key小于当前结点,所以要往当前结点左侧找;
当前节点的val < key:说明目标key大于当前结点,所以要往当前结点的右侧找;
以上内容参考了其他博主的文章,原文链接如下:
https://blog.csdn.net/qq_43591406/article/details/128852265
解题
class Solution {
public:TreeNode* deleteNode(TreeNode* root, int key) {// 递归终止的条件:遍历完整个树,没有找到目标节点,说明已经处理完了,就结束了if (root == NULL)return root;// 当前的节点的值就是目标值,有以下四种情况:if (root->val == key) {// 情况一:根节点的左子树和右子树都为空,直接删除,不改变二叉树的结构if (root->left == NULL && root->right == NULL) {delete root;return NULL;}// 情况二:右子树为空,左子树不为空,用左子树的节点代替这个节点else if (root->right == NULL) {TreeNode* retNode = root->left;delete root;return retNode;}// 情况三:左子树为空,右子树不为空,用右子树的节点代替这个节点else if (root->left == NULL) {TreeNode* retNode = root->right;delete root;return retNode;}// 情况四:左右子树都不为空,把左子树放在右子树的左孩子上,然后用右子树代替当前节点else {TreeNode* cur = root->right;while (cur->left != NULL) {cur = cur->left;}cur->left = root->left;TreeNode* tmp = root;root = root->right;delete tmp;return root;}}if (root->val > key)root->left = deleteNode(root->left, key);if (root->val < key)root->right = deleteNode(root->right, key);return root;}
};
这篇关于代码随想录算法训练营第二十二天|235. 二叉搜索树的最近公共祖先,701.二叉搜索树中的插入操作,450.删除二叉搜索树中的节点的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






