本文主要是介绍ECC椭圆曲线算法（2）初步介绍，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！
1. Weierstrass方程式
ECC(Elliptic curve cryptography) 椭圆曲线的 Weierstrass方程是一个二元三次方程:
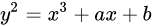且满足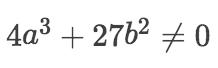 
可以看出，有3个根，其中一个为虚数。
eg.
2.定义椭圆曲线的阿贝尔群
基于椭圆曲线定义一个阿贝尔群
- 所有椭圆曲线上的点，就是这个群里的元素
- 单位元就是 0
- 点 P 的逆元是点 P 相对 x 坐标的对称点
- 加法定义：在椭圆曲线上，和一条直线相交的 3 个点 P,Q 以及 R，三点相加满足零知识证明 - 椭圆曲线基础。也就说，椭圆曲线上的两点相加的结果，还在椭圆曲线上。如果P=Q，则P+P等于P在曲线上的切线与曲线交点沿X轴的对称点。
P + Q = R
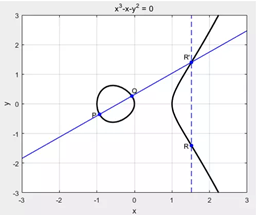
P+P=2P
2P+P=3P
3. 公私钥生成
如果我们从某一点G出发，不停做自增操作（所谓群操作，比如++），枚举出整个空间的集合元素可以用下图表示：
对应椭圆曲线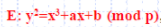
, 先得到一个随机数N作为私钥，公钥则为{E, G, Q} ,其中Q= N*G。
【参考】
[1] “最简单的椭圆曲线算法及加解密签名验签流程”. yhc166188 csdn
这篇关于ECC椭圆曲线算法（2）初步介绍的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！
