本文主要是介绍代码随想录算法训练营第二十一天| LeetCode 530.二叉搜索树的最小绝对差 、501.二叉搜索树中的众数、236. 二叉树的最近公共祖先,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
一、LeetCode 530.二叉搜索树的最小绝对差
题目链接/文章讲解/视频讲解: https://programmercarl.com/0530.%E4%BA%8C%E5%8F%89%E6%90%9C%E7%B4%A2%E6%A0%91%E7%9A%84%E6%9C%80%E5%B0%8F%E7%BB%9D%E5%AF%B9%E5%B7%AE.html状态:已解决
1.思路
这道题与LeetCode98很相似,只是它需要保证前一个节点值小于后一个节点值,而这里则是求二者差值中的最小值,二者本质都是查看中序遍历的情况下,相邻节点的值。其实昨天那个题也可以用双指针来做,但是由于稍微难理解就丢弃了那个做法,现在发现躲来躲去还是躲不掉。
二叉搜索树中的双指针法:
按照中序遍历的顺序(二叉搜索树一定是中序遍历,否则无序),prr指针指向前一个节点,cur指针指向后一个节点。然后每次递归一个节点后,将cur的值赋给pre,cur再继续递归下一个节点,那么相当于下轮递归子树时,cur指向的节点始终为pre节点的下一个节点,即二者同步移动,每次都相差一个节点。由此,可以相邻遍历完整个二叉搜索树。
注意:pre要定义在递归函数外部,因此所求值可能在右子树中取得,如果所求值始终在某子树的根节点处才能决定,那么就后序遍历并将结果变量定义为函数参数进行回溯,如果所求值在底层出现就前序遍历回溯。
2.代码实现
class Solution {
public:int result = INT_MAX;TreeNode* pre = NULL;//前一个节点保存到外面,不能作为参数传递//否则每次更新完的值由于递归特性导致又变回原来的值。void traversal(TreeNode* cur){if(cur == NULL) return ;traversal(cur->left);//前if(pre){result = min(result,cur->val-pre->val);//中}pre = cur;//节点处理依旧是在中间节点进行的,否则右子树遍历时无法将pre更新为中间结点traversal(cur->right);//后}int getMinimumDifference(TreeNode* root) {traversal(root);return result;}
};二、501.二叉搜索树中的众数
题目链接/文章讲解/视频讲解: https://programmercarl.com/0501.%E4%BA%8C%E5%8F%89%E6%90%9C%E7%B4%A2%E6%A0%91%E4%B8%AD%E7%9A%84%E4%BC%97%E6%95%B0.html状态:已解决
1.思路
这道题还是考查对二叉搜索树的掌握,跟前面的几道题差不多,第一眼还是双指针。然后cur和pre相等就将现在的计数器curNum+1,否则计数器又从1开始计;并且相等的情况下加1后还要和现在记录的最大出现值maxNum作比较,若是大于等于它就将值放入结果数组,并更新maxNum的值。这么想着,我就开始写了,写了一半发现,好像不能判断什么时候的maxNum值是最终的最大值,因此想着遍历两遍,第一遍求出maxNum的最终值,第二遍将curNum等于maxNum的值放入结果集中。
然而,看了视频之后发现这么做果然更复杂,实际我们依然可以保持原有做法,在curNum大于maxNum相等时,将值放入结果数组,只是需要在更新maxNum值的时候,将结果数组清空,这样最后在结果集中被保留下来的就是最后的答案了。
2.代码实现
class Solution {
public:vector<int> result;int maxNum = -100005;int curNum = 0;TreeNode* pre = NULL;void traversal(TreeNode* cur){if(cur == NULL) return;traversal(cur->left);if(pre == NULL) curNum=1;else if(pre->val == cur->val){curNum ++;}else{curNum = 1;}if(curNum == maxNum){result.push_back(cur->val);}if(curNum>maxNum){maxNum = curNum;result.clear();result.push_back(cur->val);}pre=cur;traversal(cur->right);}vector<int> findMode(TreeNode* root) {traversal(root);return result;}
};三、236. 二叉树的最近公共祖先
题目链接/文章讲解/视频讲解: https://programmercarl.com/0236.%E4%BA%8C%E5%8F%89%E6%A0%91%E7%9A%84%E6%9C%80%E8%BF%91%E5%85%AC%E5%85%B1%E7%A5%96%E5%85%88.html状态:已解决
1.思路
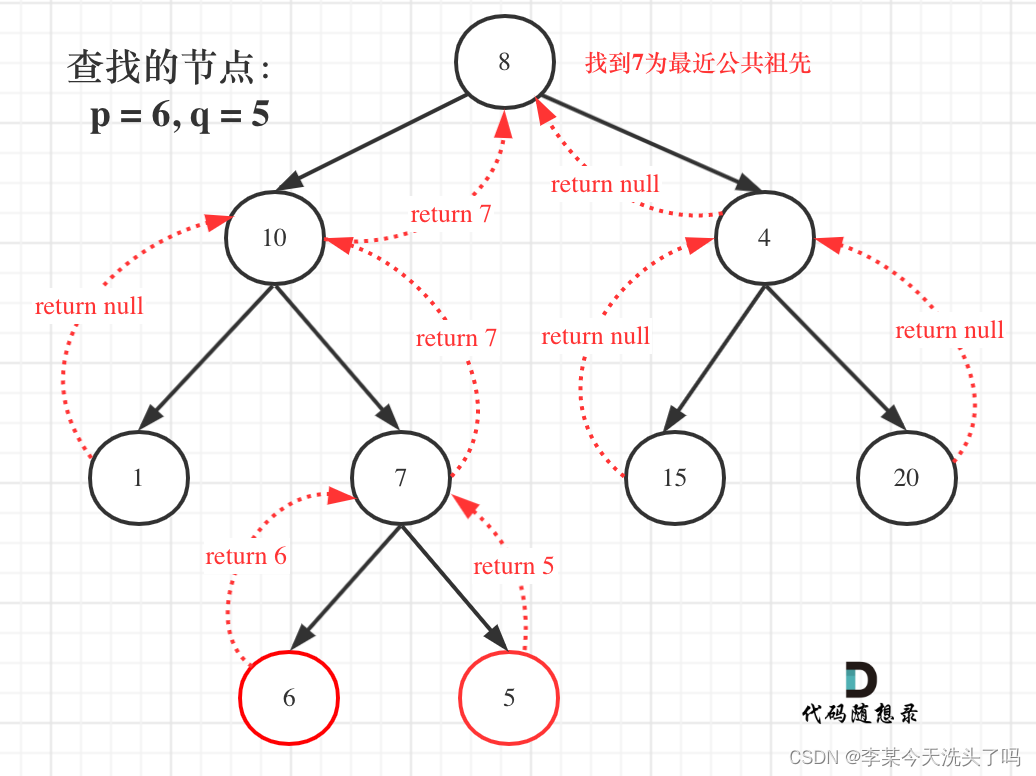
这里所求值在上层,也就是根节点处才能决定,因此要用后序遍历的方法,最后在根节点处进行判断(即用变量left、right接住返回值,这个left、right后序还有逻辑处理的需要,也就是后序遍历中处理中间节点的逻辑(也是回溯))。思路还是简单,有几个小的问题:
(1)如果left 和 right都不为空,说明此时root就是最近公共节点。这个比较好理解
(2)如果left为空,right不为空,就返回right,说明目标节点是通过right返回的,反之依然。(代表这个子树中是出现过目标节点的)
(3)left和right都为空,则说明未出现目标节点,返回空。
2.代码实现
class Solution {
public:TreeNode * result = nullptr;bool first = true;TreeNode* traversal(TreeNode* node, TreeNode* p, TreeNode* q){if(node == NULL) return NULL;if(node->val == p->val || node->val == q->val){return node;}//已经出现目标节点就要立即返回,不再向下遍历了。TreeNode* lp = traversal(node->left,p,q);//左TreeNode* rq = traversal(node->right,p,q);//右//中间处理if(lp && rq){return node;} if(lp && !rq) return lp;else if(!lp && rq) return rq;else return NULL;}TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {return traversal(root,p,q);;}
};这篇关于代码随想录算法训练营第二十一天| LeetCode 530.二叉搜索树的最小绝对差 、501.二叉搜索树中的众数、236. 二叉树的最近公共祖先的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






