本文主要是介绍Deconvolution(逆卷积),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
目前网上关于Deconvolution的文章写的着实不知所云,这里详细整理一篇出来。不敢说“一文读懂deconv”,但是“一文入门deconv”的牛还是敢吹的。
Deconvolution一般和转置卷积(transposed conv)、微步卷积(fractionally strided conv)的叫法等价,其一些常见的用途包括:
- 在ZF-Net中用于对feature map做可视化:https://arxiv.org/abs/1311.2901
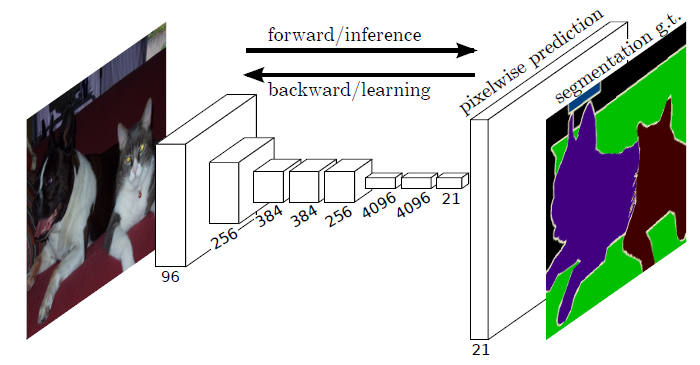
- 在FCN中用于生成等于原图shape的图像:https://arxiv.org/abs/1411.4038
- 无监督的autoencoder和deconvNet中用于解码器:https://docs.microsoft.com/en-us/cognitive-toolkit/Image-Auto-Encoder-Using-Deconvolution-And-Unpooling 、https://ftp.cs.nyu.edu/~fergus/papers/matt_cvpr10.pdf
- DSSD、GAN中的应用。
… …
由上面的用途可以看到,deconv最大的作用是对feature map进行升采样,和双线性插值(bilinear interpolation)类似。下面我们来研究一下deconv本身。顾名思义,Deconvolution(逆卷积、去卷积)似乎应该是卷积(conv)的逆过程,然而实际上除了shape层面之外,二者在数值上没有任何可逆关系。deconv仅仅是一个普通的卷积层,在神经网络中也是需要通过梯度下降去学习的。所以,对于每个deconv层,我们实际上也能用另外一个deconv层去做恢复。(突然有个发现——如果用conv+deconv进行穿插排列组合是不是也能创造出许多新的网络架构emmm)
PyTorch代码见:https://pytorch.org/docs/stable/nn.html?highlight=trans#torch.nn.ConvTranspose2d。
核心原理
关于deconv的恢复原理,最核心的一条其实就是 (k-1) \textbf{(k-1)} (k-1)扩展(padding),来重要的事情说三遍: (k-1) \textbf{(k-1)} (k-1)扩展, (k-1) \textbf{(k-1)} (k-1)扩展, (k-1) \textbf{(k-1)} (k-1)扩展。不明白?先背下来再往下看。
最基本的形式
我们首先看看最基本的卷积形式:对于 ( m × m ) (m\times m) (m×m)特征图 I I I,用 ( k × k ) (k\times k) (k×k)的核做卷积,则得到的特征图 O O O是 ( m − k + 1 ) × ( m − k + 1 ) (m-k+1)\times(m-k+1) (m−k+1)×(m−k+1)。如果我们对 O O O做 (k-1) \textbf{(k-1)} (k-1)扩展得到 O ′ O' O′,再用等大的 k × k k\times k k×k核做卷积,则得到的特征图 I ′ I' I′边长是: ( m − k + 1 ) + 2 ( k − 1 ) − k + 1 = m (m-k+1)+2(k-1)-k+1=m (m−k+1)+2(k−1)−k+1=m。示意图:
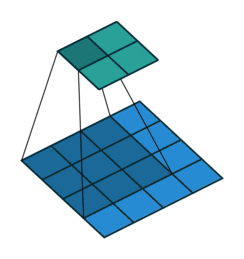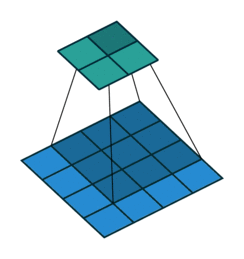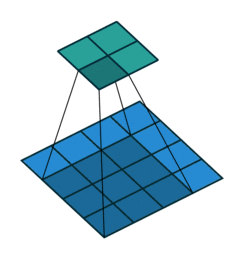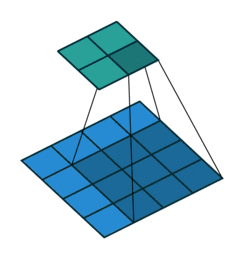
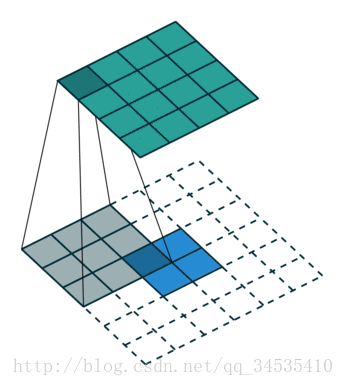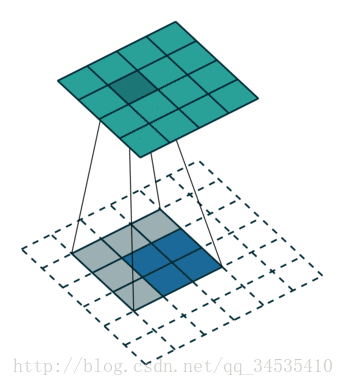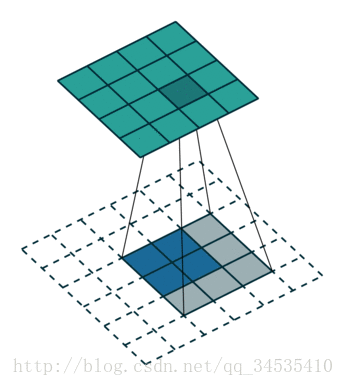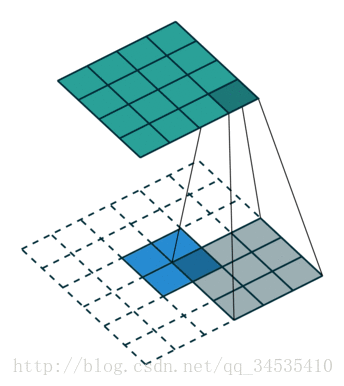
如果加入了stride呢?
然后我们来看看加入stride之后的deconv。同样,对于 ( m × m ) (m\times m) (m×m)特征图 I I I,用 ( k × k ) (k\times k) (k×k)的核做卷积,计stride为 s s s。则得到的特征图 O O O是 ( m − k s + 1 ) × ( m − k s + 1 ) (\dfrac{m-k}{s}+1)\times(\dfrac{m-k}{s}+1) (sm−k+1)×(sm−k+1)。同样,我们对 O O O做 (k-1) \textbf{(k-1)} (k-1)扩展,再用等大的 k × k k\times k k×k核做卷积。和上面不同的是,这次我们加入相同的stride,也就是对 O O O做膨胀得到 O ′ O' O′(抱歉我想不到更合适的词了,见下面的示意图),卷积过程中卷积核不做跨步。 O ′ O' O′的边长是 ( m − k s + 1 ) + 2 ( k − 1 ) + ( s − 1 ) ( m − k s + 1 − 1 ) (\dfrac{m-k}{s}+1)+2(k-1)+(s-1)(\dfrac{m-k}{s}+1-1) (sm−k+1)+2(k−1)+(s−1)(sm−k+1−1),化简得到 ( m + k − 1 ) (m+k-1) (m+k−1)。则用等大的 ( k × k ) (k\times k) (k×k)核做卷积之后同样能恢复原来的shape m m m。当然了,此处令 s = 1 s=1 s=1则能推出前一段的特殊情况。
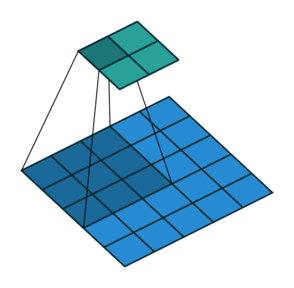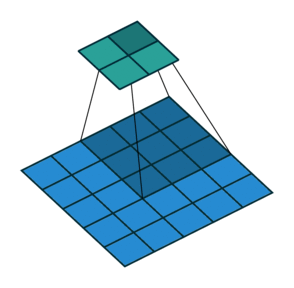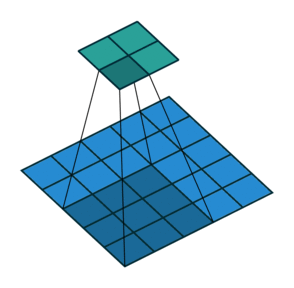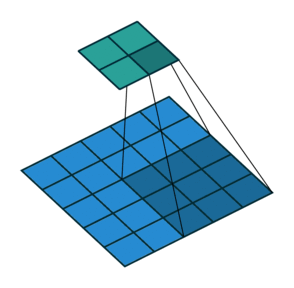
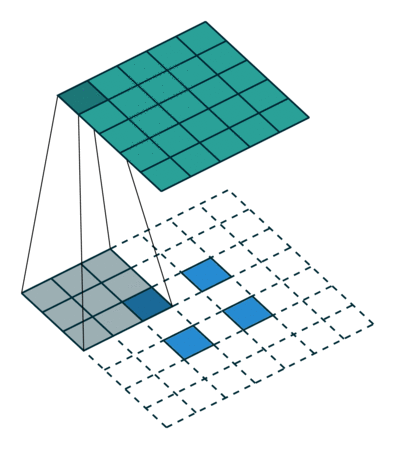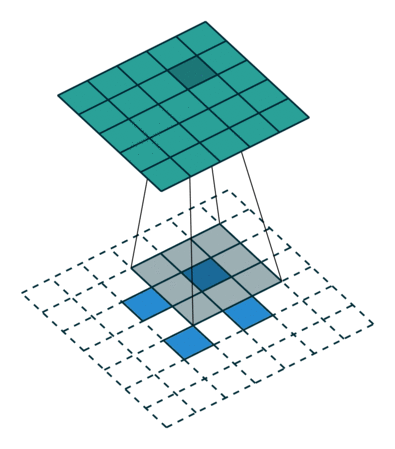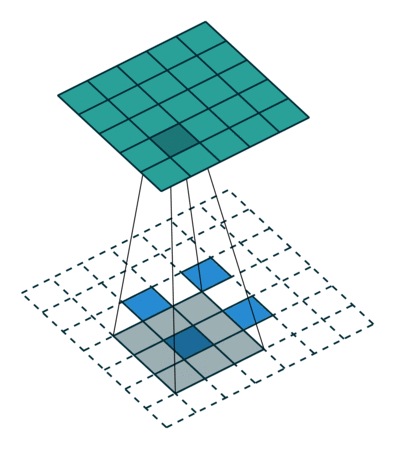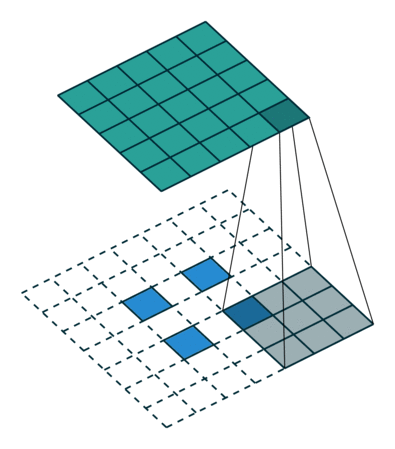
如果加入了padding呢?
好了,我们现在似乎已经对于deconv的可逆原理有了一定的了解。于是问题来了,加入pad之后呢?道理其实是一样的,我们只需要把上面的 m m m换成 m + 2 p m+2p m+2p即可。下面我们来算一下stride 1的情况:
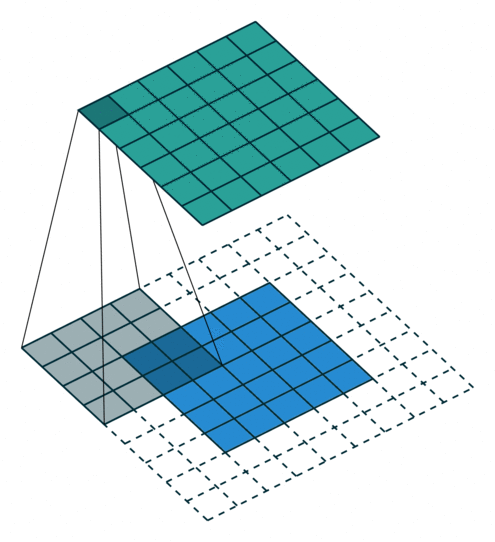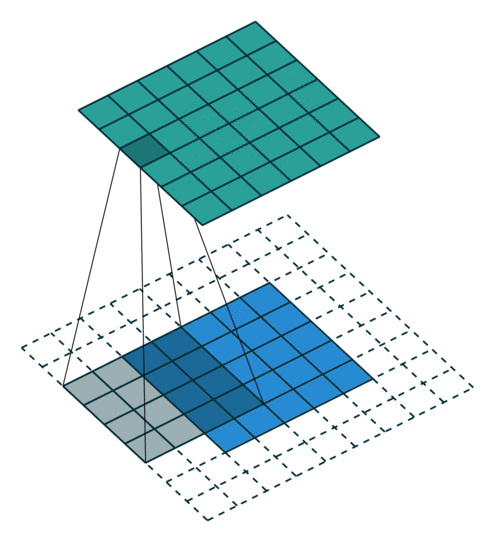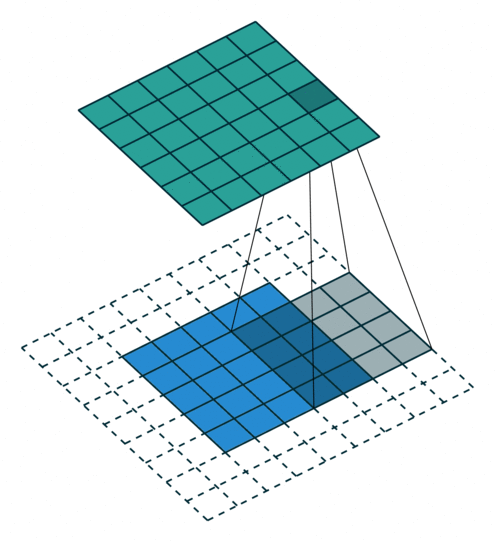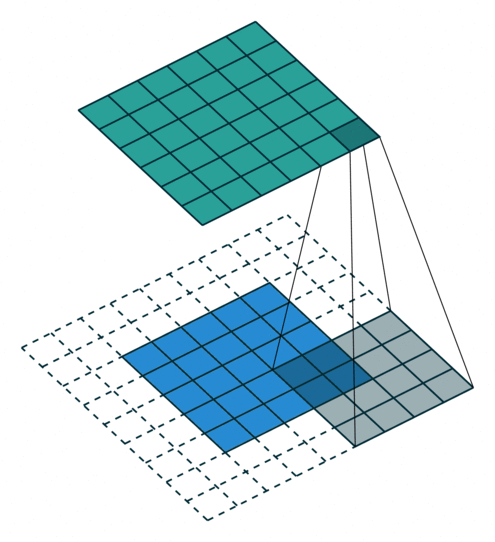
对于 ( m × m ) (m\times m) (m×m)特征图 I I I,先pad p p p,用 ( k × k ) (k\times k) (k×k)的核做卷积,则得到的特征图 O O O是 ( m + 2 p − k + 1 ) × ( m + 2 p − k + 1 ) (m+2p-k+1)\times(m+2p-k+1) (m+2p−k+1)×(m+2p−k+1)。如果我们对 O O O做 p ′ p' p′扩展得到 O ′ O' O′,再用等大的 k × k k\times k k×k核做卷积,则得到的特征图 I ′ I' I′边长是: ( m + 2 p − k + 1 ) + 2 p ′ − k + 1 = m (m+2p-k+1)+2p'-k+1=m (m+2p−k+1)+2p′−k+1=m。
所以有:
2 p − 2 k + 2 + 2 p ′ = 0 2p-2k+2+2p'=0 2p−2k+2+2p′=0
p ′ = k − 1 − p p'=k-1-p p′=k−1−p
所以第一节的核心原理要更新一下——做扩展 p ′ = k − 1 − p p'=k-1-p p′=k−1−p之后再卷积。如图:
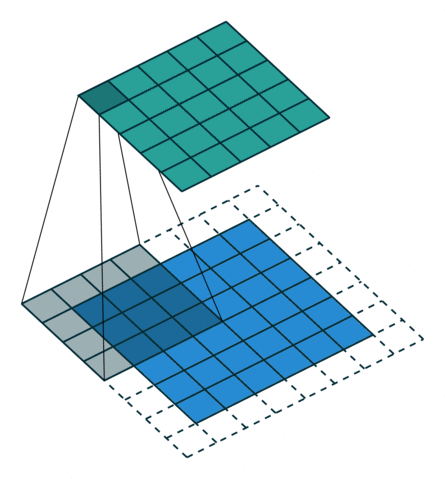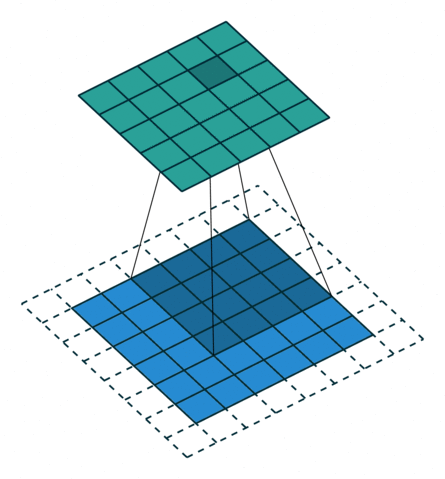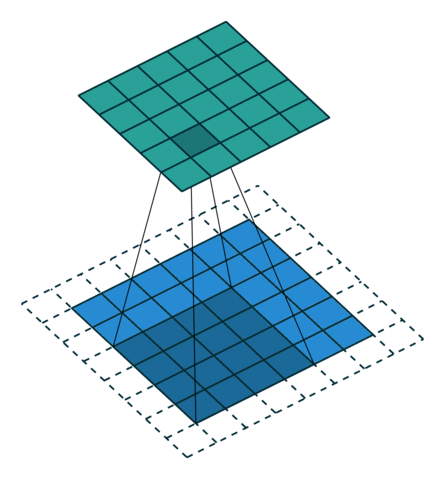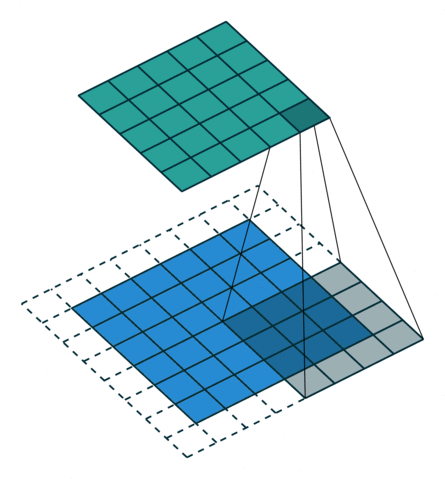
如果是最一般的形式,即既有padding,又有stride呢?
道理其实是一样的。这里大概列一个计算步骤,详细过程感兴趣的朋友可以自己推一遍。
特征图 I I I: m × m m\times m m×m
做pad得到 I ′ I' I′: ( m + 2 p ) × ( m + 2 p ) (m+2p)\times (m+2p) (m+2p)×(m+2p)
卷积后得到特征图 O O O: ( m + 2 p − k s + 1 ) × ( m + 2 p − k s + 1 ) (\dfrac{m+2p-k}{s}+1)\times(\dfrac{m+2p-k}{s}+1) (sm+2p−k+1)×(sm+2p−k+1)
做pad p ′ p' p′得到 O ′ O' O′: ( m + 2 p − k s + 1 + 2 p ′ ) × ( m + 2 p − k s + 1 + 2 p ′ ) (\dfrac{m+2p-k}{s}+1+2p')\times(\dfrac{m+2p-k}{s}+1+2p') (sm+2p−k+1+2p′)×(sm+2p−k+1+2p′)
做stride s s s得到 O ′ ′ O'' O′′: ( m + 2 p − k s + 1 + 2 p ′ + ( s − 1 ) ( m + 2 p − k s + 1 − 1 ) ) × ( m + 2 p − k s + 1 + 2 p ′ + ( s − 1 ) ( m + 2 p − k s + 1 − 1 ) ) (\dfrac{m+2p-k}{s}+1+2p'+(s-1)(\dfrac{m+2p-k}{s}+1-1))\times(\dfrac{m+2p-k}{s}+1+2p'+(s-1)(\dfrac{m+2p-k}{s}+1-1)) (sm+2p−k+1+2p′+(s−1)(sm+2p−k+1−1))×(sm+2p−k+1+2p′+(s−1)(sm+2p−k+1−1))
deconv之后得到的特征图 I ′ ′ I'' I′′边长是: O ′ ′ 的 边 长 − k + 1 O''的边长-k+1 O′′的边长−k+1
令 I ′ ′ I'' I′′边长为 m m m。解得 p ′ = k − 1 − p p'=k-1-p p′=k−1−p
To do
空洞卷积(dilated convolution)、从矩阵乘法的角度理解卷积和逆卷积。
ref:
https://github.com/vdumoulin/conv_arithmetic
这篇关于Deconvolution(逆卷积)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!