本文主要是介绍深度学习启蒙:神经网络基础与激活函数,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
目录
1.引言
2.神经网络架构与前向传播
2.1. 神经网络架构
2.2. 前向传播
3.常见激活函数公式与图像
3.1. sigmoid函数
3.2. tanh函数
3.3. ReLU函数
3.4. Leaky ReLU
3.5. Softmax函数
4.激活函数可视化比较与选择
4.1激活函数对比图像
4.1激活函数的选择策略
4.1.1 训练稳定性
4.1.2 计算效率
4.1.3 初始化权重
5.总结
1.引言
深度学习作为人工智能领域的一个重要分支,近年来取得了显著的进展。神经网络作为深度学习的核心组成部分,其设计和优化对于提高模型的性能至关重要。在神经网络的构建中,激活函数的选择和应用是一个不可忽视的环节。
激活函数为神经网络引入了非线性特性,使得网络能够学习和表示复杂的数据模式。不同的激活函数具有不同的数学特性和适用场景,因此选择适合特定任务的激活函数对于提高神经网络的性能至关重要。
本文旨在介绍神经网络的基础架构以及常见的激活函数,并探讨如何根据实际应用场景选择适合的激活函数。首先,我们将介绍神经网络的基本组成和前向传播过程,为后续讨论激活函数打下基础。接着,我们将详细解析几种常见的激活函数,包括Sigmoid、ReLU和Tanh等,并分析它们的数学特性、优缺点以及适用场景。最后,我们将探讨在选择激活函数时需要考虑的因素,包括训练稳定性、计算效率以及权重初始化等。
通过本文的学习,读者将能够深入了解神经网络的基本架构和激活函数的作用原理,掌握常见激活函数的特性和选择方法,并能够在实际应用中根据需求灵活选择和调整激活函数,以提高神经网络的性能。更多Python在人工智能中的使用方法,欢迎关注《Python人工智能实战》专栏!
2.神经网络架构与前向传播
2.1. 神经网络架构
神经网络是一种模仿人脑神经元结构与功能的计算模型,由大量相互连接的简单处理单元(神经元)组成。其基本架构包括输入层、隐藏层和输出层:
- 输入层:接收原始数据,每个神经元对应一个输入特征。
- 隐藏层:中间处理层,对输入进行非线性变换,提取抽象特征。层数和神经元数量可自由设定,增加层数和神经元数量可提升模型表达能力。
- 输出层:生成最终预测或分类结果,神经元数量取决于任务需求(如回归任务通常为1个神经元,多分类任务为类别数个神经元)。
神经元之间通过加权连接传递信息,每个连接对应一个权重参数,表示输入对该神经元的影响程度。
2.2. 前向传播
前向传播是神经网络中数据从输入层流向输出层的过程。每个神经元接收来自前一层神经元的加权输入,经过激活函数的处理,然后输出到下一层。这个过程可以表示为数学运算,通过矩阵乘法和激活函数的应用实现。前向传播是神经网络从输入到输出的计算过程,具体步骤如下:
- 输入层:将输入数据传递给输入层神经元。
- 隐藏层:对于每个隐藏层神经元,计算其所有输入神经元与之相连的加权和,加上偏置项,然后通过激活函数进行非线性变换。
- 输出层:对输出层神经元执行与隐藏层相同的操作,得到最终输出结果。
数学表达式为:
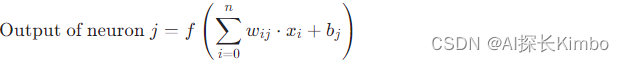
其中,xi 是神经元 i 的输入,wij 是连接神经元 i 到神经元 j 的权重,bj 是神经元 j 的偏置,f 是激活函数。
3.常见激活函数公式与图像
激活函数是神经网络中至关重要的非线性变换元件,它赋予网络模型处理非线性关系的能力。以下是几种常见的激活函数:
3.1. sigmoid函数

优点:输出范围在(0, 1)内,易于解释为概率;光滑连续,便于梯度传播。
缺点:饱和区梯度接近于0,可能导致梯度消失;输出不是以0为中心,不利于权重更新。
import numpy as np
import matplotlib.pyplot as plt def sigmoid(x): return 1 / (1 + np.exp(-x)) x = np.linspace(-10, 10, 100)
y = sigmoid(x) plt.plot(x, y)
plt.title('Sigmoid Activation Function')
plt.xlabel('Input')
plt.ylabel('Output')
plt.grid(True)
plt.show()上述代码绘制了Sigmoid函数的图像。从图像中可以看出,当输入值趋近于正无穷或负无穷时,输出值趋近于1或0,而在原点附近,输出值变化较快。
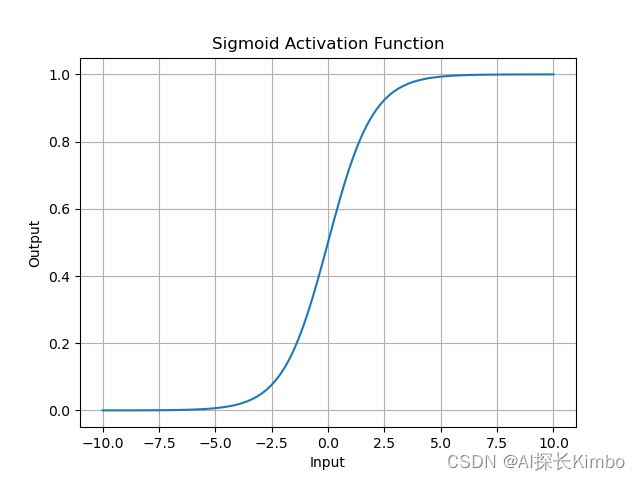
3.2. tanh函数

优点:输出范围在(-1, 1)内,比sigmoid更利于权重更新;也是光滑连续的。
缺点:饱和区同样存在梯度消失问题。
import numpy as np
import matplotlib.pyplot as pltdef tanh(x):return np.tanh(x)x = np.linspace(-10, 10, 100)
y = tanh(x)plt.plot(x, y)
plt.title('Tanh Activation Function')
plt.xlabel('Input')
plt.ylabel('Output')
plt.grid(True)
plt.show()Tanh函数的图像类似于Sigmoid函数,输出范围在-1到1之间。从图像中可以看出,当输入值趋近于正无穷或负无穷时,输出值趋近于1或-1,而在原点附近,输出值变化较快。
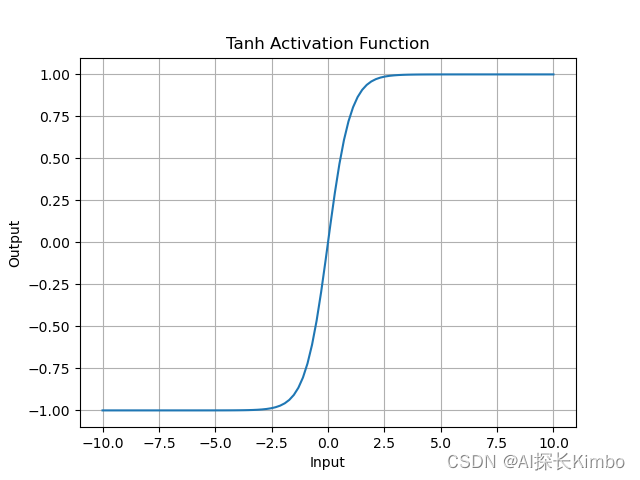
3.3. ReLU函数

优点:简单、计算效率高;在正区间内梯度恒为1,有效缓解梯度消失问题。
缺点:输出非零中心,可能导致权重更新偏向;存在“死区”(输入小于0时梯度为0),可能导致神经元失效。
import numpy as np
import matplotlib.pyplot as pltdef relu(x):return np.maximum(0, x)x = np.linspace(-10, 10, 100)
y = relu(x)plt.plot(x, y)
plt.title('ReLU Activation Function')
plt.xlabel('Input')
plt.ylabel('Output')
plt.grid(True)
plt.show()ReLU函数的图像在x轴以上为直线,x轴以下为水平线。当输入为正数时,输出与输入相同;当输入为负数时,输出为0。

3.4. Leaky ReLU
Leaky ReLU是ReLU函数的一个变体,旨在解决ReLU在训练过程中可能出现的神经元“死亡”问题。它允许小的负梯度通过,从而保持神经元在负输入时的活性。
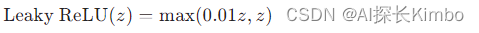
优点:解决了ReLU的“死区”问题,对负输入也有一定响应。
缺点:需要人为设定斜率参数,可能不如ReLU简单。
import numpy as np
import matplotlib.pyplot as pltdef leaky_relu(x, alpha=0.01):return np.maximum(alpha * x, x)x = np.linspace(-10, 10, 100)
y = leaky_relu(x)plt.plot(x, y)
plt.title('Leaky ReLU Activation Function')
plt.xlabel('Input')
plt.ylabel('Output')
plt.grid(True)
plt.show()Leaky ReLU函数的图像在x轴以上为直线(斜率为1),与ReLU类似;在x轴以下,函数有一个小的正斜率(由参数alpha决定),使得输出不为零。这种设计使得Leaky ReLU在负输入时仍然具有一定的梯度,有助于防止神经元“死亡”。
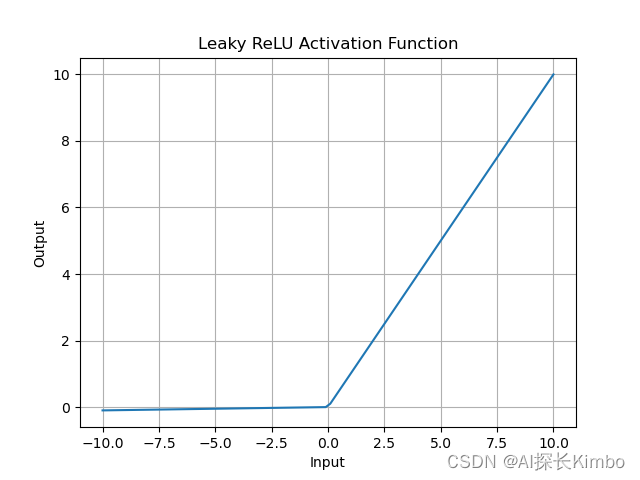
3.5. Softmax函数
Softmax函数常用于多分类问题的输出层,它将神经网络的原始输出转换为概率分布,其公式为:

import numpy as np def softmax(x): exps = np.exp(x - np.max(x)) return exps / np.sum(exps) # 示例:假设神经网络对三个类别的原始输出为 [3, 1, 0.2]
scores = np.array([3, 1, 0.2])
probabilities = softmax(scores) print("原始输出:", scores)
print("概率分布:", probabilities)
# 原始输出: [3. 1. 0.2]
# 概率分布: [0.8360188 0.11314284 0.05083836] Softmax函数将神经网络的原始输出(通常称为分数或对数几率)转换为概率分布。在这个例子中,原始输出为[3, 1, 0.2],经过Softmax函数处理后,得到了对应的概率分布。这些概率值在0到1之间,并且所有类别的概率之和为1。这有助于解释神经网络对于不同类别的预测置信度。
4.激活函数可视化比较与选择
为了直观理解不同激活函数的特性,本节我在同一张图像中绘制了它们的函数图像。这些图像揭示了激活函数如何对输入进行非线性变换以及它们各自的饱和区域、梯度变化趋势等关键信息。
4.1激活函数对比图像
使用matplotlib库绘制sigmoid、tanh、ReLU、Leaky ReLU和softmax函数的图像。
import matplotlib.pyplot as plt
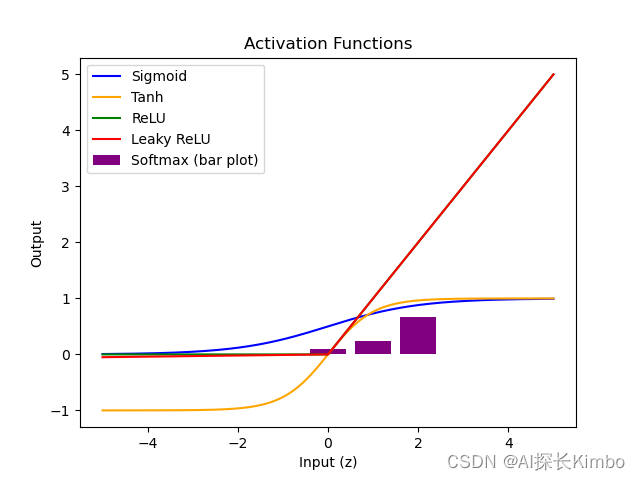
import numpy as npdef plot_activation_functions():x = np.linspace(-5, 5, 1000)# Sigmoid functiony_sigmoid = 1 / (1 + np.exp(-x))plt.plot(x, y_sigmoid, label='Sigmoid', color='blue')# Tanh functiony_tanh = np.tanh(x)plt.plot(x, y_tanh, label='Tanh', color='orange')# ReLU functiony_relu = np.maximum(0, x)plt.plot(x, y_relu, label='ReLU', color='green')# Leaky ReLU functionalpha = 0.01y_leaky_relu = np.maximum(alpha * x, x)plt.plot(x, y_leaky_relu, label='Leaky ReLU', color='red')# Softmax function (for a single input)z = np.array([1, 2, 3])z_exp = np.exp(z)softmax = z_exp / np.sum(z_exp)plt.bar(range(len(softmax)), softmax, label='Softmax (bar plot)', color='purple')plt.title('Activation Functions')plt.xlabel('Input (z)')plt.ylabel('Output')plt.legend()plt.show()plot_activation_functions()运行上述代码会生成一个包含五种激活函数图像的图表:
- Sigmoid:呈现S形曲线,两端平缓上升至饱和,中间陡峭变化,输出范围(0, 1)。
- Tanh:双曲正切函数,形状类似sigmoid但中心对称,输出范围(-1, 1)。
- ReLU:线性函数在x轴上方,x轴下方为常数0,不存在饱和区,梯度在正区间内恒为1。
- Leaky ReLU:与ReLU相似,但在x轴下方有斜率为α的直线,避免完全“死亡”。
- Softmax:以条形图形式展示,输入向量经过指数运算和归一化后转化为概率分布,各元素和为1。
4.1激活函数的选择策略
回归任务通常不需要激活函数(或使用线性激活),分类任务通常使用sigmoid(二分类)或softmax(多分类)在输出层。对于深层网络,优先选用ReLU及其变种以避免梯度消失问题。
在选择激活函数时,除了考虑它们的数学特性和应用场景外,还需要考虑以下几点:
4.1.1 训练稳定性
不同的激活函数在训练过程中可能表现出不同的稳定性。例如,ReLU函数可能导致神经元“死亡”,而Sigmoid和Tanh函数则可能由于梯度消失问题导致训练困难。因此,在选择激活函数时,需要权衡这些因素,并根据具体任务进行调整。
4.1.2 计算效率
激活函数的计算效率也是需要考虑的因素之一。例如,ReLU函数由于其简单的计算方式,通常比Sigmoid和Tanh函数具有更高的计算效率。在构建大型神经网络或处理大规模数据集时,计算效率尤为重要。
4.1.3 初始化权重
激活函数的选择还与网络权重的初始化有关。不同的激活函数可能对权重的初始化有不同的要求。因此,在选择激活函数时,需要考虑如何合理地初始化网络权重,以确保网络的稳定训练。
5.总结
综上所述,理解神经网络的架构、前向传播过程以及激活函数的特性与选择策略,是深度学习启蒙阶段的关键知识。在实践中,应结合具体任务、数据特性和资源限制,灵活运用并不断探索优化激活函数的选择与使用。 更多Python在人工智能中的使用方法,欢迎关注《Python人工智能实战》专栏!
这篇关于深度学习启蒙:神经网络基础与激活函数的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




