【最近公共祖先】浅论lca

本文主要是介绍【最近公共祖先】浅论lca，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

lca

lca(Least Common Ancestors)。顾名思义，就是离两个点最近的公共祖先，换句话说，就是在一棵树中，两个点最短距离中的深度最小的点。

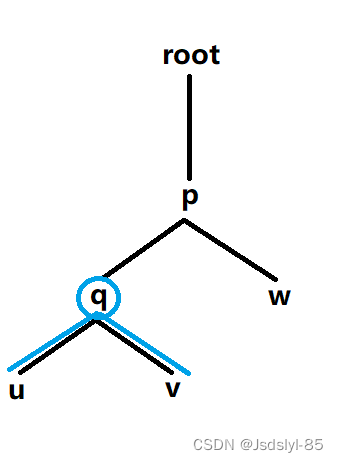
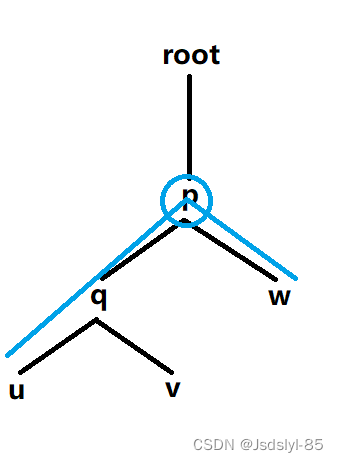
图1 图2

如图所示，在图1中，u和v的lca为q；在图2中，u和w的lca为p。

特别的，节点本身也可以做祖先，如u和q的lca为q。

不难看出，lca可以用作查询树中两点之间最短距离，即计算根节点到两节点u和v的距离是 $S_{u}$ 和 $S_{v}$ ，并算出根节点到它们lca的距离 $S_{lca(u,v)}$ ，于是可以推出 $(L_{u\rightarrow v})_{min}=S_{u}+S_{v}-2S_{lca(u,v)}$

代码实现

如果用暴力做法，面对严格的时间条件必然是不行的，它的时间复杂度往往不能满足需求。因此，我们需要一些更为巧妙的方法：

1. 倍增思想

倍增法通俗的来讲就是每一步尽可能跳的多一点。假设我们要求解 $lca(u,v)$ ，最为直截了当的做法就是始终将深度较深的往上跳跃一步，直到u,v的深度第一次相等时，那么该节点就是 $lca(u,v)$ 。但是这样做的话时间复杂度是 $\Theta (n)$ 的，面对多组查询的情况，那就完蛋了。

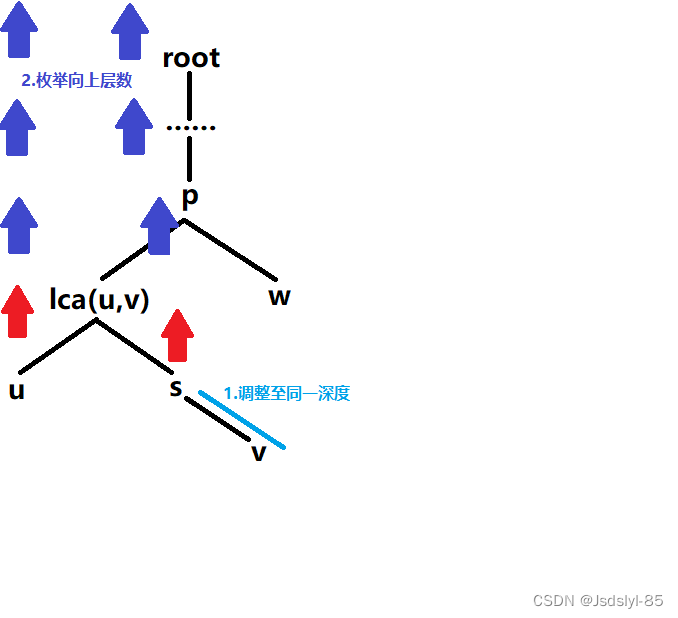
其实，可以让两个节点同时上升，直到相遇为止。那么就要先把u和v置于同一层，将深层节点上移至与浅层节点相同的层数即可。此时上升层数 $\Delta depth=dep_{lca(u,v)}-dep_{u}=dep_{lca(u,v)}-dep_{v}$ （此时u和v处于同一层）。面对未知深度的 $lca(u,v)$ ，我们就需要枚举 $\Delta depth$ 尝试。综合来看，枚举向上 $2^{i}$ 步最佳。

那又出现了一个问题，调了 $2^{k}$ 步之后，达到了u和v的公共祖先，但是这可能并不是n和v的最近公共祖先——跳“过去”了。为了避免这种情况，我们选择从大到小枚举，直到j==0跳出循环，若跳跃 $2^{i}$ 步仍然不同则继续跳跃……

跳跃操作是通过动态规划实现的。用 $f[i][j]$ 表示节点i的跳跃j步，可以由子问题推导出，容易看出 $f[i][j]=f[f[i][j-1]][j-1]$ ，可以预处理。

于是可以得到：

预处理：

void dfs(int u,int fa)
{dep[u]=dep[fa]+1;for(int i=head[u];i!=0;i=e[i].next){int j=e[i].v;if(j==fa)continue;f[j][0]=u;for(int k=1;(1<<k)<=dep[u];k++)f[j][k]=f[f[j][k-1]][k-1];dfs(j,u);}
}

lca的实现：

int lca(int x,int y)
{if(dep[x]<dep[y])swap(x,y);for(int i=19;i>=0;i--)if(dep[f[x][i]]>=dep[y])x=f[x][i];//将两点置于同一深度if(x==y)return y;//若两点相同，即为共同祖先，而此时深度为min(dep[x],dep[y])，所以为lca(u,v)，直接返回for(int i=19;i>=0;i--)//枚举i，跳跃2^i步if(f[x][i]!=f[y][i])x=f[x][i],y=f[y][i];//同步倍增return f[y][0];返回父亲节点（向上跳2^0=1层到达父节点）
}

这里的19是因为作者做的一道题节点数小等于500000个， $19=\left \lceil {log_{2}}^{500000} \right \rceil$ 。所以这里的数字就是 $\left \lceil {log_{2}}^{n} \right \rceil$ （n为节点总数）

此处用链式前向星（邻接表）存树，再次为大家奉上代码：

const int z=500010;
struct edge
{int v,next;
}e[2*z];
void addedge(int u,int v)
{idx++;e[idx].v=v;e[idx].next=head[u];head[u]=idx;
}//链式前向星

预处理时间复杂度是 $\Theta (n{log_{2}}^{n})$ ，每次查询时间复杂度是 $\Theta ({log_{2}}^{n})$ ，查询m次，则整体的时间复杂度是 $\Theta (n{log_{2}}^{n}+m{log_{2}}^{n})$ ，对比暴力的 $\Theta (n^{2}+nm)$ 确乎是快了不少！
上述算法主要有3个核心部分