本文主要是介绍传递函数极点和零点的几何表示,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
1. 系统的极点和零点
传递函数为确定重要的系统响应特性提供了不需要求解完整的微分方程的理论。
复数 s = ρ + jω
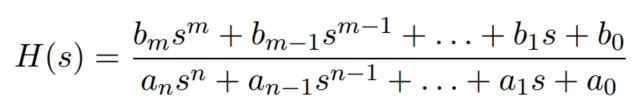
可以写成
![]()
z1 z2...zm 为零点 H(s) -> 0
p1 p2 ...pn为极点 H(s) - > ∞
example1:
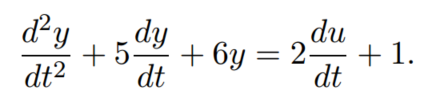
传递函数为
2 s + 1
H(s) = -------------
s^2 + 5 s + 6
1 s + 1/2
H(s) = --- ---------------------
2 (s-(-3))(s-(-2))
零点 s = -1/2
极点 s = -3 和 s = -2
example2:
一个系统,极点为 p1 ,p2 = -1±j2 ,一个零点为 z = -4,增益 K = 3, 则 系统响应函数为:
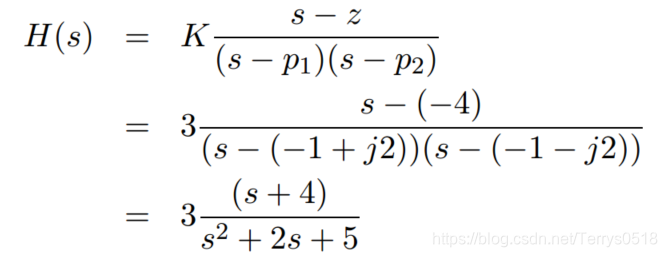
等效的微分方程
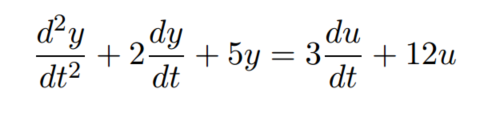
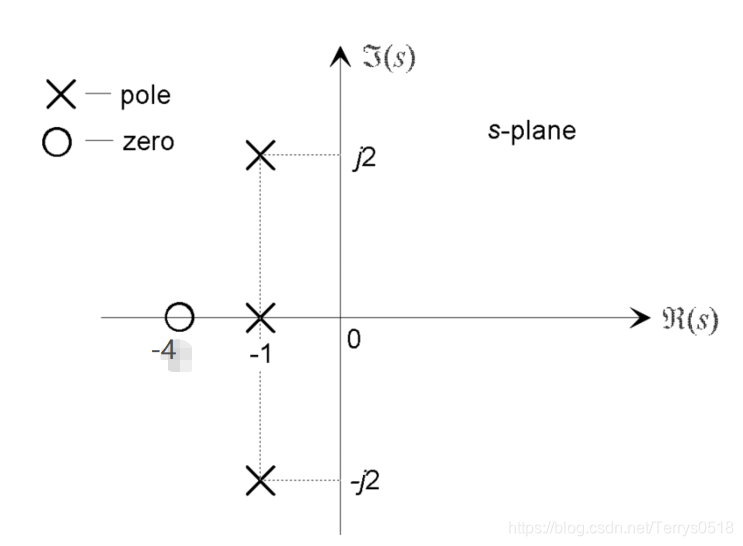
2. 传递函数的几何分析
对于复数函数,可以等效为向量的表示方法
![]()
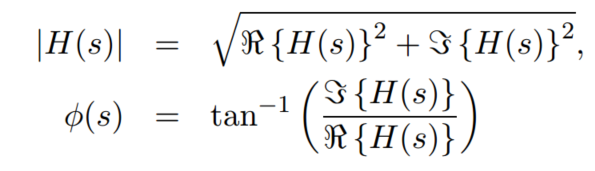
对于
![]()
分母的每一项,都可以表示成:
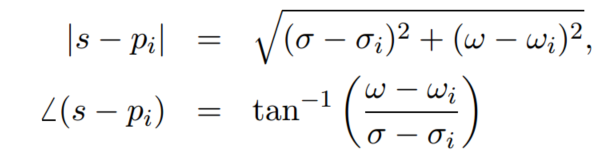
因此
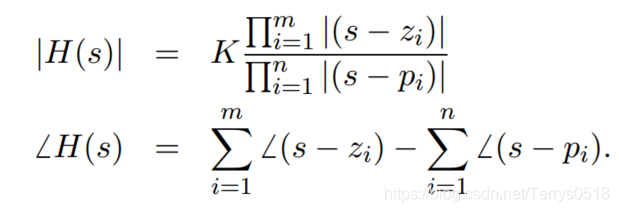
example:
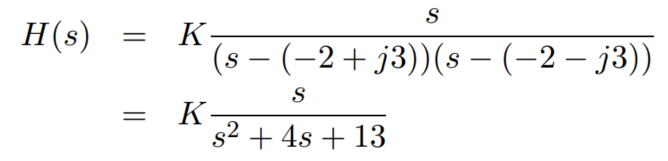
当s = 0 + j5 时
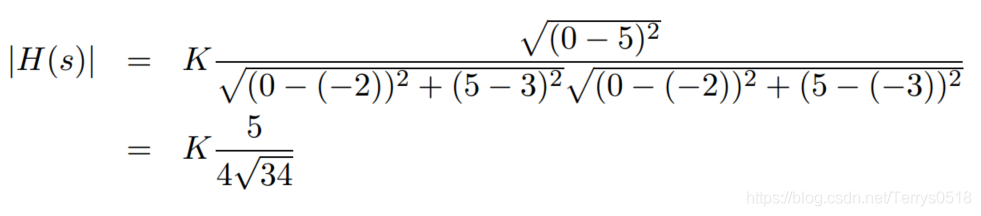
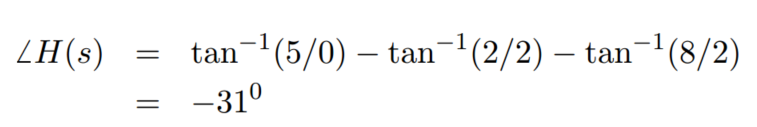
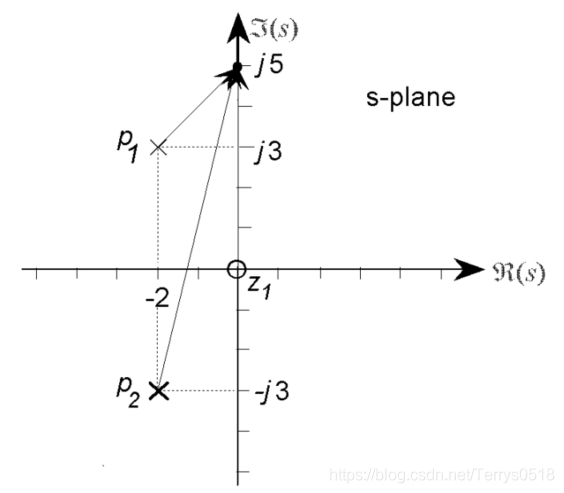
因此 传递函数的响应特性,可以从图上表示出来 对某一个信号的增益,相位的改变,都可以用作图的方法分析,简单又直观。
这篇关于传递函数极点和零点的几何表示的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!