ACWING 3774 亮灯时长

点击查看原题

题意：

     从0时刻开电闸并开灯，到M时刻关电闸，期间可以按n次灯的开关，每次按开关灯的状态都会变一下（亮变灭，灭变亮），你可以选择再按一次或者不按，使得亮灯时长最长（选择按的时间不能等于已给定的时间）。

做法：

     可以任选一个满足条件的位置按开关，此开关之前的区域不变，此开关之后的位置变换状态。这里可以用后缀和来做。分两个区域，一个是不按开关亮的区域，用数组s1表示，另一个是不按开关灭的区域，用数组s2表示。

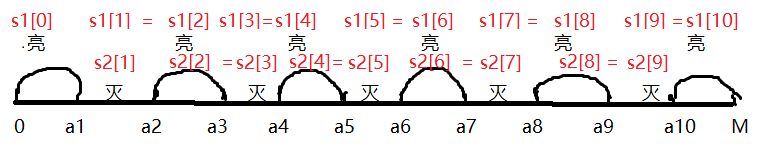
 不管在哪个区域按，都要使按的那个区域亮灯时长最大，即使得t=a[i]-a[i-1]-1;s1[0]是不改变的时候亮灯时长总和，改变之后就为  改变区域之前亮的时长加上改变区域之后区域灭的时长

 具体代码如下：

#include <iostream>
#include <cstring>
#include <cstdio>
using namespace std;
const int N=1e5+10;
int a[N];
int s1[N],s2[N];
int main()
{int T;scanf("%d",&T);while(T--){int n,M;scanf("%d%d",&n,&M);for(int i=1;i<=n;i++){scanf("%d",&a[i]);}a[++n]=M;  s1[n]=s2[n]=0;for(int i=n-1;i>=0;i--){s1[i]=s1[i+1],s2[i]=s2[i+1];if(i%2==0) s1[i]+=a[i+1]-a[i];else s2[i]+=a[i+1]-a[i];  //求出原始状态下的亮灯和灭灯时长后缀和}int res=s1[0];for(int i=0;i<n;i++){int t=a[i+1]-a[i];if(t<=1) continue;res=max(res,s1[0]-s1[i]+s2[i+1]+t-1);//更新最长亮灯时长}printf("%d\n",res);}return 0;
}