概率论总结（四）：矩母函数（含证明，超级简单明了！）

目录：

• 定义
• 常见随机变量的矩母函数
  - 泊松随机变量的矩母函数
  - 二项随机变量的矩母函数
  - 几何随机变量的矩母函数
  - 指数随机变量的矩母函数
  - 随机变量线性函数的矩母函
  - 正态分布随机变量的矩母函数
  - 均匀随机变量的矩母函数
• 从矩母函数到矩
• 矩母函数的可逆性
• 独立随机变量和
• 汇总

矩母函数（Moment Generating Function） 是对概率(分布列或者概率密度函数)的另一种表述。它并不是特别直观的, 但是在解决某些类型的数学计算时很方便。

定义：


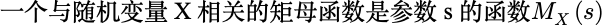
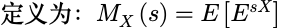
随机变量是 X 时,矩母函数也可以简记为M(s)。
当 X 是离散随机变量时,相关矩母函数为：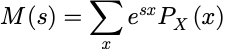
当 X 是连续随机变量时,相关矩母函数为：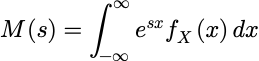
例：

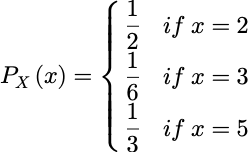
其相应的矩母函数为：

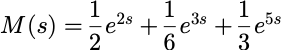
常见随机变量的矩母函数

💁泊松随机变量的矩母函数

设随机变量 X 服从参数为λ的泊松分布：

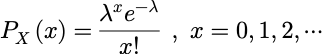
其矩母函数为：



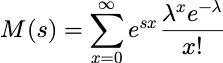
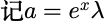
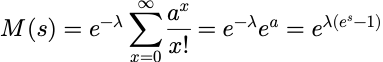
💁二项随机变量的矩母函数
设随机变量X服从二项分布：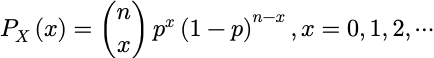
其矩母函数为：（最后一个括号上的次方应该是n,打错了。）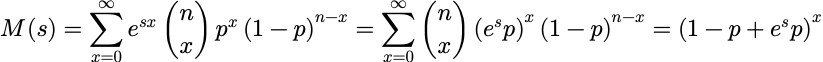
💁几何随机变量的矩母函数
设随机变量X服从几何分布：

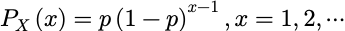
其矩母函数为：

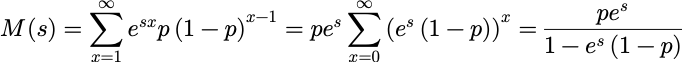
最后一个等式用了下式：

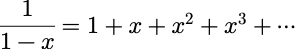
💁指数随机变量的矩母函数

设随机变量 X 服从参数为λ 的指数分布：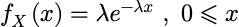
则：

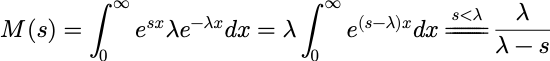
以上运算和M(s)的公式仅在 s<λ下成立, 否则积分为无穷.
重要的是要认识到矩母函数不是一个数而是一个参数为 s 的函数。

💁随机变量线性函数的矩母函数

M(s)记为随机变量 X 的矩母函数,考虑新随机变量Y=aX+b的矩母函数.由矩母函数定义, 有:

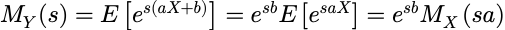
例如,如果 X 服从参数λ=1的指数分布, 则:

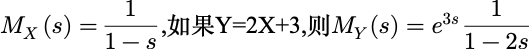
💁正态分布随机变量的矩母函数

记 X 为服从均值为 μ、方差为σ^2 的正态随机变量。为了计算它的矩母函数, 首先我们考虑标准正态随机变量 Y 的情况,对 Y有均值为0且方差为1。求出 Y 的矩母函数以后, 再导出X 的矩母函数.
标准正态分布的概率密度函数为：

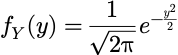
则矩母函数为：


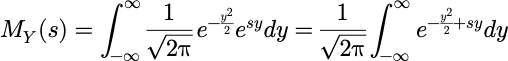
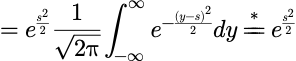
*：利用了服从均值为 s 方差为1的正态随机变量的概率密度函数的归
一化性质.
均值为μ方差为σ^2 的正态随机变量可表成标准正态随机变量的线性函数：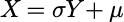
利用随机变量线性函数的矩母函数：

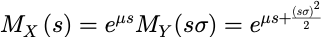
💁均匀随机变量的矩母函数

区间[a,b]上均匀分布的连续 随机变量 X 的矩母函数:

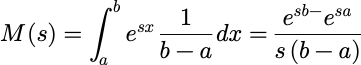
离散情况下：
设X 分布列是　：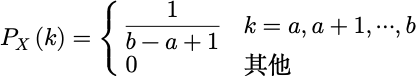
其矩母函数为：

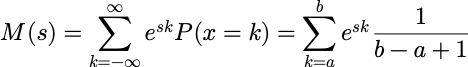
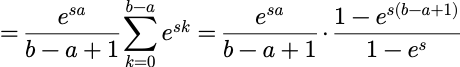
从矩母函数到矩

“矩母函数”这一名称是由于随机变量的矩可以通过矩母函数的公式轻易计算出而得来的.为验证这一点, 现在考虑一个连续随机变量 X,根据定义：

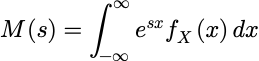
式两边取 s 的导数：

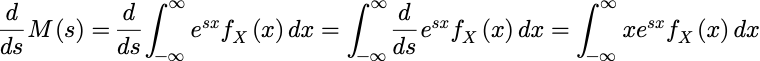
考虑s=0这种情况：

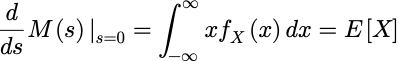
更一般的，如果我们对M(s)取 n 次 s 的导数, 通过类似的计算有:

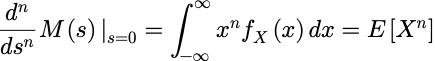
例：指数随机变量的概率密度函数为：

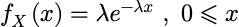
矩母函数为：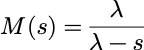
因此：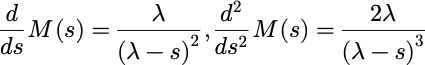
令s=0,有：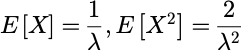
矩母函数的两个十分有用的性质

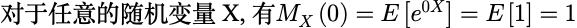
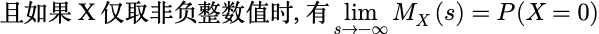
矩母函数的可逆性

矩母函数的一个非常重要的性质是它可逆,即可用它来确定随机变量 X的概率律.
矩母函数可逆的条件：
假定随机变量 X 的矩母函数M(s)满足：存在一个正数 a,对在区间[-a,a]中的任意 s, M(s)都是有限的, 则矩母函数M(s)唯一地决定 X 的分布函数.
例：已知随机变量 X 的相关矩母函数为：



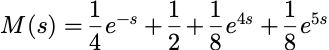
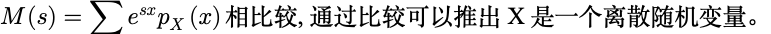
X 的取值范围可以从相应的 指数读出来,即-1、0、4、5.
每个 x 值的概率可以从e^(sx)前面乘的系数得到.
即：

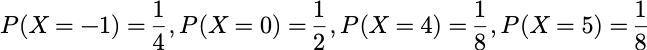
例：(几何随机变量的矩母函数)　已知随机变量 X 的矩母函数为：

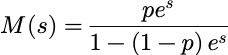
这里 p 是一个常数, 且（0<p<=1），我们想要求出 X 的分布.由几何级数公式得：

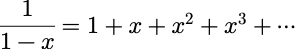
上式对于任意满足｜x｜<1的 x都成立.

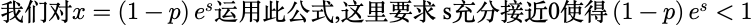
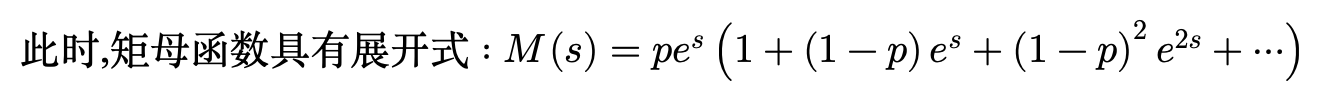
将这个式子与上例中一般离散随机变量的矩母函数的表达式比较,可知 M(s)所对应的随机变量是取正整数值的离散型随机变量. 概率P(X=k) 可以通过读取e^(sx)的系数得到.
具体来说,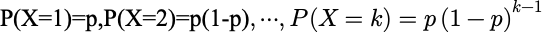
可见这个分布正是参数为 p 的几何分布.
注意:

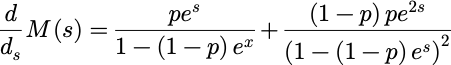
当 s=0时,右边等于1/p,即E[X]=1/p,与之前推导的结果一样。

独立随机变量和

独立随机变量的和 的矩母函数是和项的矩母函数的乘积.
记 X 和 Y 为独立的随机变量, 并记Z=X+Y根据定义, Z 的矩母函数为:

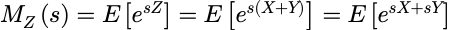
因为 X 和 Y 是独立的, 对于任意的 s，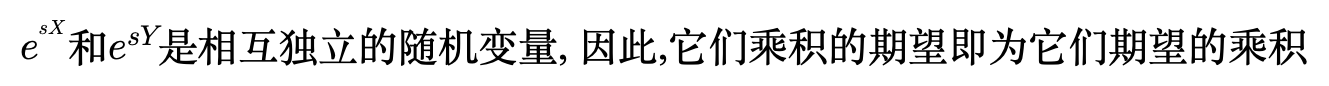

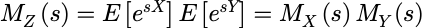
同样地, 如果X1，X2，…，Xn是独立的随机变量,且Z=X1+X2+…+Xn
相应的矩母函数之间有下面的关系：

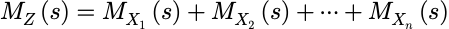
💁二项随机变量的矩母函数
设X1，X2，…，Xn为独立的伯努利随机变量, 参数都为p. 按定义,不难得到

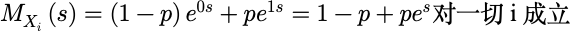
随机变量Z=X1+X2+…+Xn服从参数为 n 和 p 的二项分布,相应的矩母函数为:

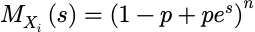
汇总

常见的离散随机变量的矩母函数：
参数为 p 的伯努利分布（k=0,1）


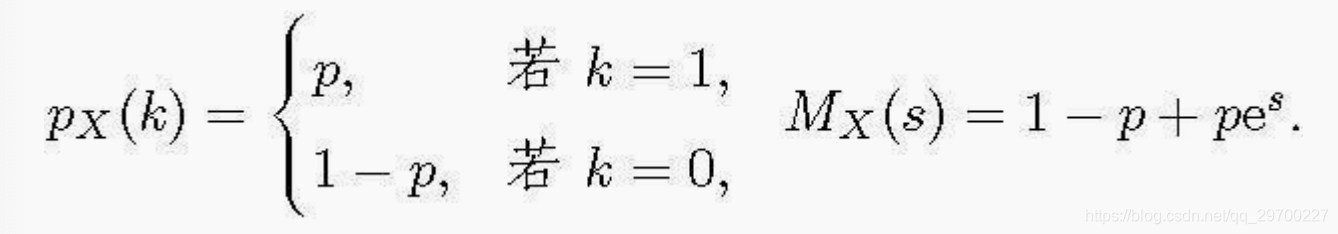
常见连续随机变量的矩母函数: