本文主要是介绍重心坐标,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
重心坐标
三角形内部点p的性质:



P的重心坐标:
坐标系角度求解
以a点为原点,ab,ac分别为新的坐标系的单位向量构建坐标系

定任意点P的坐标可以用 β , γ来表示,即 P(β,γ),
则

==>>

基底坐标变换
将该坐标 𝑥 从基底 𝑈 迁移到基底𝑉,得到新的坐标值
假设二维空间𝑅2存在标准基为{ e 1 e_1 e1, e 2 e_2 e2},任何𝑅2中的向量 p p p 都可
以表示为线性组合: p = x e 1 + y e 2 p=xe_1+ye_2 p=xe1+ye2。标量 x x x 和 y y y 可以看成是 p p p 在
标准基下的坐标。
对任意𝑅2的基 { A B ⃗ \vec{AB} AB, A C ⃗ \vec{AC} AC} ,给定向量 p p p可唯一地表示为线性组合: p = β A B ⃗ + γ A C ⃗ p=β\vec{AB}+γ\vec{AC} p=βAB+γAC,标量(β,γ)为 p p p相应于基{ A B ⃗ \vec{AB} AB, A C ⃗ \vec{AC} AC}的坐标。
对于二维列向量,对应到空间中的坐标是(x, y),其实就是基于默认基底:
二维基向量的完整表达就应该是


如图

向量(4,1),在标准坐标系下坐标为4和1, 在基底向量为(1,2)和(3,-1)的坐标系下坐标为1和1
可以看出标准坐标系下的向量左乘 以两个新基底坐标构成的矩阵的逆, 就是在新坐标系下的坐标
由此可推出,在以a为坐标系原点,ab和ac为新的基底坐标下的坐标P(β,γ),与标准坐标系下的坐标P的关系为

可得出两个二元一次方程,求解可求出β和γ的值,根据1-β-γ的出三个系数

代数求解

可分解为

根据

消除 α \alpha α

两个二元一次方程
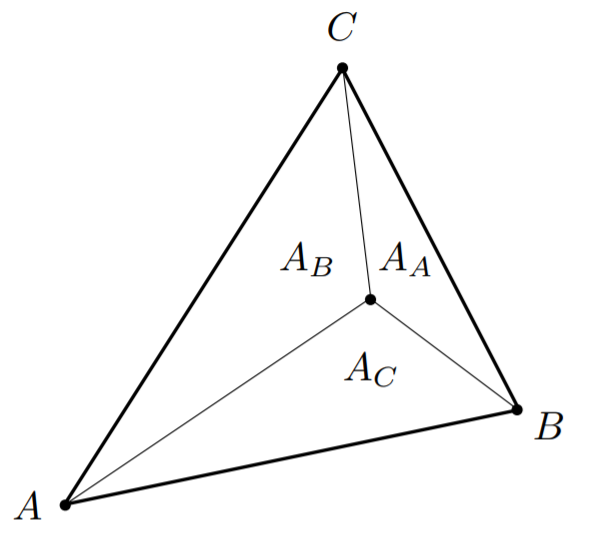
几何面积求解




可根据查处求三角形面积,根据各三角形面积的比求出三个系数
应用
由此可以通过三角形内任一点P(x,y),根据重新坐标求解三个系数 i,j,k
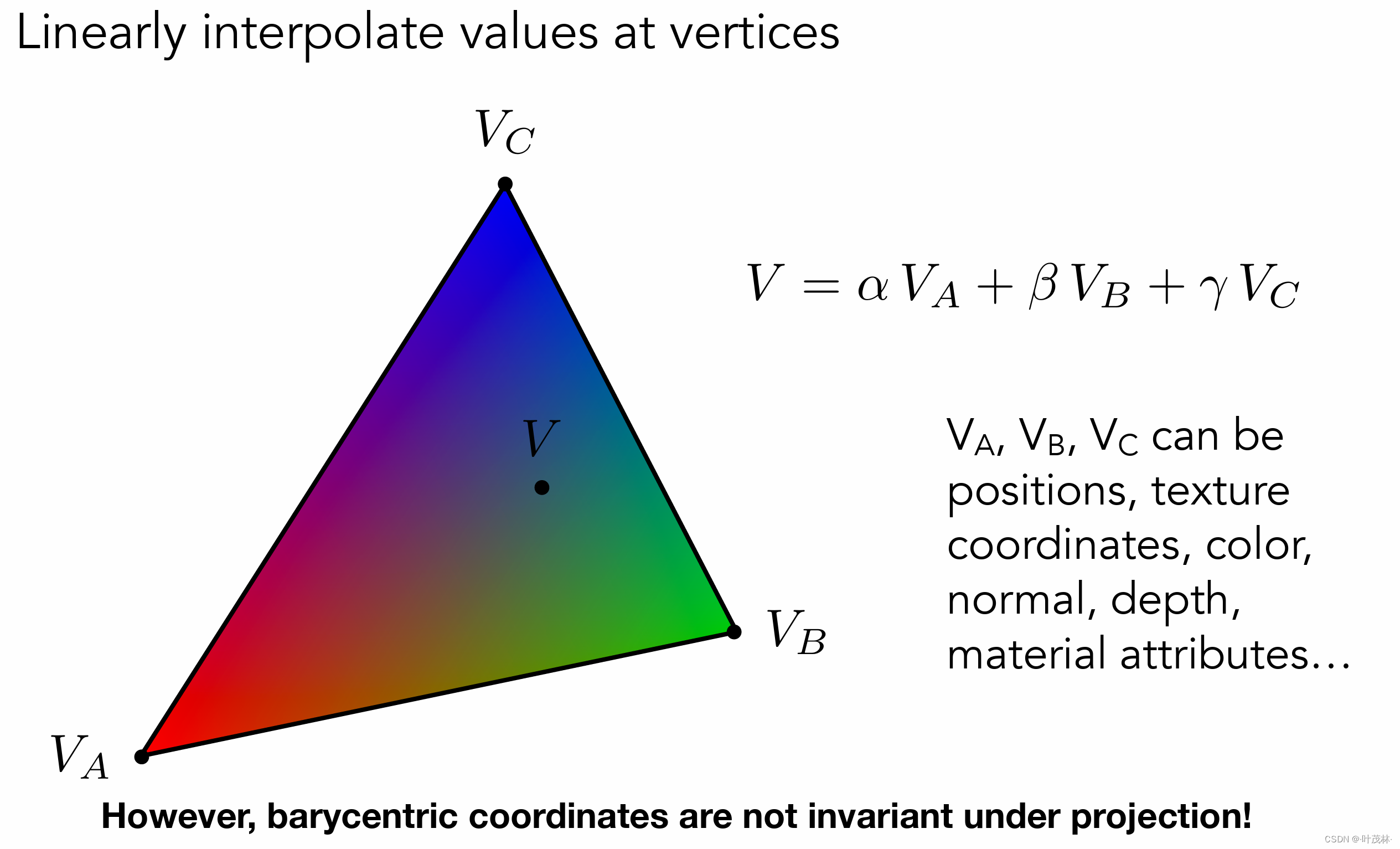
P = iA + jB + kC
ABCP代表的都是位置信息,但可以把ABCD的信息用别的任何信息来代替,例如颜色,法线,uv,深度等,然后套用上面的公式即可求出P点对应的属性
- 若 i,j,k均大于0,则点 在三角形内部
- 若其中一个为0,则点 在三角形的边或边的延长线上
- 若其中两个为0,则 在三角形的一个顶点上。利用这个性质,可以判断射线是否与三角形相交
参考文章
这篇关于重心坐标的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!